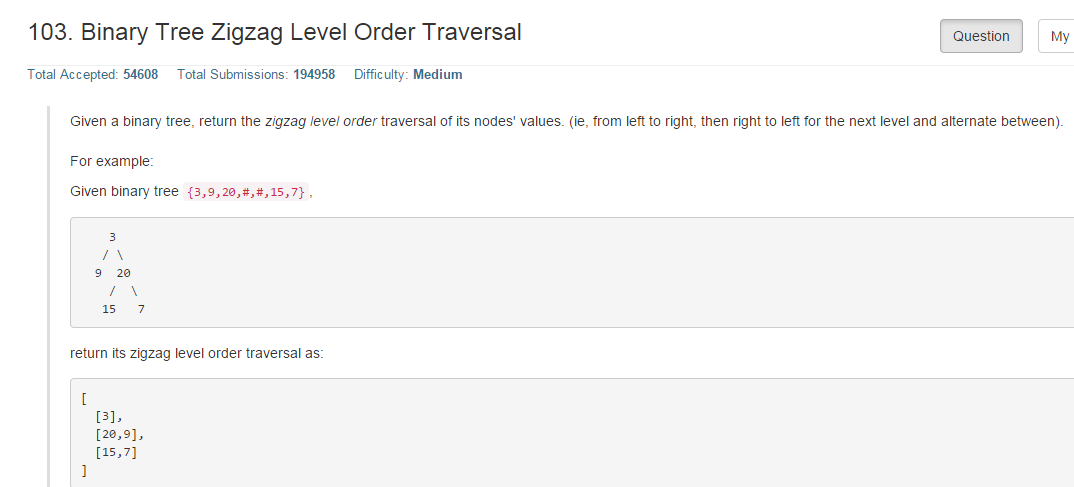
103. Binary Tree Zigzag Level Order Traversal
题目
分析:
广度优先遍历的应用。重点是掌握vector的reverse函数,一开始我忘记有这个函数了,琢磨半天都没弄出来,后来想起reverse函数,问题一下子就迎刃而解。
代码
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 vector<vector<int>> zigzagLevelOrder(TreeNode* root) { 13 vector<vector<int>> res; 14 vector<int> temp; 15 if(NULL == root) 16 return res; 17 18 queue<TreeNode*> myQue; 19 TreeNode *temp1; 20 bool flag = true; 21 myQue.push(root); 22 23 while (!myQue.empty()) 24 { 25 temp.clear(); 26 myQue.push(NULL); 27 temp1 = myQue.front(); 28 myQue.pop(); 29 while (NULL != temp1) 30 { 31 temp.push_back(temp1->val); 32 if(NULL != temp1->left) 33 myQue.push(temp1->left); 34 if(NULL != temp1->right) 35 myQue.push(temp1->right); 36 temp1 = myQue.front(); 37 myQue.pop(); 38 } 39 if(!flag) 40 { 41 reverse(temp.begin(),temp.end()); 42 } 43 44 res.push_back(temp); 45 flag = (!flag); 46 } 47 } 48 49 };
---------------------------------------------------------------------------------------分割线-------------------------------------------------------------------------
104. Maximum Depth of Binary Tree
题目
分析:
求树的深度,递归。代码如下:
1 /** 2 * Definition for binary tree 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 int maxDepth(TreeNode *root) { 13 if(NULL == root)return 0; 14 int min1=0; 15 int min2=0; 16 min1 = maxDepth(root->left); 17 min2 = maxDepth(root->right); 18 19 return (min1>min2 ? min1:min2)+1; 20 21 22 } 23 };
----------------------------------------------------------------------------------------分割线----------------------------------------------------------------------------------
105. Construct Binary Tree from Preorder and Inorder Traversal
题目;
分析:
题目要求利用前序、中序遍历构造一棵二叉树。
基本思想:通过前序遍历数组,找到当前子树的根节点在中序遍历数组中的下标,然后将中序遍历数组一分为二,一部分为左子树,一部分为右子树。递归调用构造完整的二叉树。
其中存在特殊情况,某个节点没有左子树,或者没有右子树,或者左右子树都不存在。
代码如下
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) { 13 int size = preorder.size(); 14 if(0 == size) 15 return NULL; 16 //TreeNode *root = myBuild(preorder,inorder,0,0,size-1);这里不能直接传0,因为参数是引用 17 int index = 0; 18 TreeNode *root = myBuild(preorder,inorder,index,0,size-1); 19 } 20 TreeNode* myBuild(vector<int>& preorder, vector<int>& inorder,int& index,int start,int end)//index为什么要用引用 21 { 22 //if(start == end) 23 //{ 24 // return new TreeNode(inorder[start]); 25 //} 26 int i=start; 27 //for(;i<inorder.size();i++) 28 for(;i<=end;i++) 29 { 30 if(inorder[i] == preorder[index]) 31 break; 32 } 33 34 TreeNode *temp = new TreeNode(preorder[index]); 35 if(i == start)//当前节点没有左子树 36 temp->left = NULL; 37 else 38 temp->left = myBuild(preorder,inorder,++index,start,i-1); 39 if(i == end)//当前节点没有右子树 40 temp->right = NULL; 41 else 42 temp->right = myBuild(preorder,inorder,++index,i+1,end); 43 44 return temp; 45 } 46 };
----------------------------------------------------------------------------分割线----------------------------------------------------------------
106. Construct Binary Tree from Inorder and Postorder Traversal
题目
分析:
通过二叉树的中序遍历和后序遍历来构造二叉树。
基本思想:通过后序遍历数组,找到当前子树的根节点在中序遍历数组中的下标,然后将中序遍历数组一分为二,一部分为左子树,一部分为右子树。递归调用构造完整的二叉树。
比较105和106题。可以发现,中序遍历数组在整个构造二叉树过程中起着"分岭"作用,如果只有前序和后序遍历,构造二叉树就比较麻烦了。
需要了解的是后序遍历数组中,最后一个节点就是当前子树的根节点,所以代码实现是从后序遍历数组的尾部开始,从后往前的遍历。
代码如下:
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) { 13 int size = postorder.size(); 14 if(0 == size) 15 return NULL; 16 TreeNode *root = myBuild(inorder,postorder,0,size-1,size-1); 17 } 18 //函数每次从postorder的尾部开始遍历,也就是从后往前遍历,参数index是指向当前需要访问postorder中的最后一个元素 19 TreeNode* myBuild(vector<int>& inorder, vector<int>& postorder,int start,int end,int index)//start,length是用于inorder数组中的, 20 { 21 //if(start == end) 22 //{ 23 // return new TreeNode(inorder[start]); 24 //} 25 int i=start; 26 //for(;i<inorder.size();i++) 27 for(;i<=end;i++) 28 { 29 if(inorder[i] == postorder[index]) 30 break; 31 } 32 //找到i下标,将inorder分为两部分,一部分是左子树,一部分是右子树 33 TreeNode *temp = new TreeNode(postorder[index]); 34 if(i == start)//当前节点没有左子树 35 temp->left = NULL; 36 else 37 temp->left = myBuild(inorder,postorder,start,i-1,index-(end-i)-1);//index-(end-i)-1是左子树的根节点在postorder中的下标 38 if(i == end)//当前节点没有右子树 39 temp->right = NULL; 40 else 41 temp->right = myBuild(inorder,postorder,i+1,end,index-1);//index-1是右子树的根节点在postorder中的下标 42 43 return temp; 44 } 45 };


