39、Combination Sum
题目

题目要求找出和为target的数字组合,并且每个整数可以多次使用。仔细思考可以发现,这道题目可以采用递归的方法来完成,比如举的例子,target=7,一开始可以选中2,并且2<7,因此,我只需要从[2,3,6,7]中寻找和为5(因为可以重复选择整数,因此需要从2开始而不是从下一个数3开始),如果后面的结果中找不出和为5,因此需要剔除当前选择的2,从下一个数3开始,按照这个递归继续执行。这样就把规模变小,代码如下:
class Solution { public: vector<vector<int>> combinationSum(vector<int>& candidates, int target) { vector<int> temp; vector<vector<int>> res; sort(candidates.begin(), candidates.end()); combinationSum(candidates,0,temp,res,target); return res; } void combinationSum(const vector<int>& candidates,int start,vector<int> &temp,vector<vector<int>> &res,int target) { if (0 == target) { res.push_back(temp); } for (int i=start;i<candidates.size();i++) { if(candidates[i]<=target) { temp.push_back(candidates[i]); combinationSum(candidates,i,temp,res,target-candidates[i]); temp.pop_back(); } } } };
--------------------------------------------------------------------------------------------分割线--------------------------------------------------------------------------------
40、Combination Sum II
题目
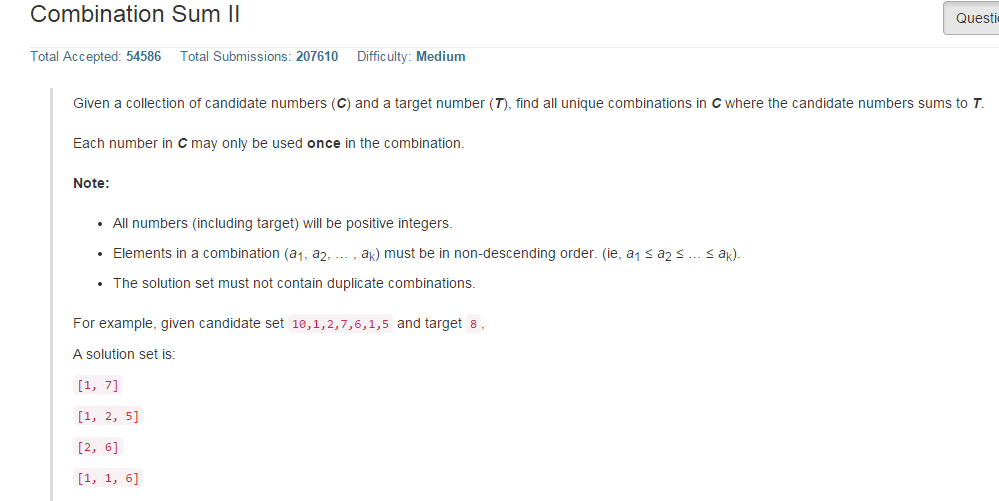
这道题和上一题差别不到,唯一的差别就是每个数至多使用一次,因此在之前的代码中需要做一次数据过滤,代码如下:
1 class Solution { 2 public: 3 vector<vector<int>> combinationSum2(vector<int>& candidates, int target) { 4 vector<int> temp; 5 vector<vector<int>> res; 6 sort(candidates.begin(), candidates.end()); 7 combinationSum(candidates,0,temp,res,target); 8 return res; 9 } 10 11 void combinationSum(const vector<int>& candidates,int start,vector<int> &temp,vector<vector<int>> &res,int target) 12 { 13 if (0 == target) 14 { 15 16 res.push_back(temp); 17 } 18 19 for (int i=start;i<candidates.size();i++) 20 { 21 22 if(candidates[i]<=target) 23 { 24 temp.push_back(candidates[i]); 25 combinationSum(candidates,i+1,temp,res,target-candidates[i]); 26 temp.pop_back(); 27 while(i+1<candidates.size() && candidates[i] == candidates[i+1])//跳过后续相同的整数 28 i++; 29 } 30 } 31 } 32 };
----------------------------------------------------------------------------------分割线------------------------------------------------------------------------------------------
41、First Missing Positive
题目

这道题目技巧性很强,在网上查看资料之后才知道如何解答。其解答的思路是:如果0<nums[index]<size,就将nums[index]这个值交换到对应下标所在的空间去。比如题目中的[3,4,-1,1],一开始index=0,其值为3,因此将3交换到index=2(3-1)去,变成[-1,4,3,1],代码如下:
1 class Solution { 2 public: 3 int firstMissingPositive(vector<int>& nums) { 4 const int size = nums.size(); 5 if(0 == size) 6 return 1; 7 int i,index; 8 int temp; 9 for (i = 0;i<size;i++) 10 { 11 index=i; 12 while(nums[index]>0&&nums[index]<size&&nums[index] != index+1) 13 { 14 if(nums[nums[index]-1] == nums[index]) 15 break; 16 temp = nums[nums[index]-1]; 17 nums[nums[index]-1] = nums[index]; 18 nums[index] = temp; 19 } 20 } 21 for(i = 0;i<size;i++) 22 { 23 if(i+1 != nums[i]) 24 return i+1; 25 } 26 if(i == size) 27 return size+1; 28 29 } 30 };


