29、Divide Two Integers
题目

题目要求不用乘除和取模运算,实现两个整数相除;
我的第一想法就是把除法变成减法来做,这也是最初除法的定义,其实现代码如下:
1 class Solution { 2 public: 3 int divide(int dividend, int divisor) { 4 if(1 == divisor) 5 return dividend; 6 if (-1 == divisor) 7 return 0-dividend; 8 9 bool flag = false; 10 11 if((dividend<0&&divisor>0)) 12 { 13 dividend = 0-dividend; 14 flag = true; 15 } 16 else if(dividend>0&&divisor<0) 17 { 18 divisor = 0-divisor; 19 flag = true; 20 } 21 22 dividend = abs(dividend); 23 divisor = abs(divisor); 24 25 26 int result = 0; 27 while (dividend >=divisor) 28 { 29 dividend -= divisor; 30 result++; 31 } 32 if(flag) 33 result = 0 - result; 34 35 return result; 36 37 } 38 };
看似没什么问题,但是其效率是不高的,比如被除数很大,而除数很小的时候,while循环会执行很多次,导致其效率不高,因此需要想想其他的办法解决该问题;既然直接做减法会超时,那姑且只能想移位操作了,因为移位操作是比较高效的操作,能够快速得到想要结果。如果是移位操作,应该如何下手呢?任何一个整数可以表示成以2的幂为底的一组基的线性组合,即num=a_0*2^0+a_1*2^1+a_2*2^2+...+a_n*2^n,在做除法时,dividend/divisor = num,变换一下就可以写成这样dividend = divisor*(a_0*2^0+a_1*2^1+a_2*2^2+...+a_n*2^n);因此先让divisor左移n位,然后用dividend减去这个数,剩下的结果继续用同样的方法求解n-1,代码如下:
1 class Solution { 2 public: 3 int divide(int dividend, int divisor) { 4 // Note: The Solution object is instantiated only once. 5 long long a = abs((double)dividend); 6 long long b = abs((double)divisor); 7 long long res = 0; 8 while(a >= b) 9 { 10 long long c = b; 11 for(int i = 0; a >= c; i++, c <<=1) 12 { 13 a -= c; 14 res += 1<<i; 15 } 16 } 17 18 19 if((dividend ^ divisor) >> 31) 20 res = 0-res; 21 if(res >= 2147483647) 22 return 2147483647; 23 else 24 return res; 25 26 } 27 };
---------------------------------------------------------------------------------------------分割线--------------------------------------------------------------------------------
30、Substring with Concatenation of All Words
题目:
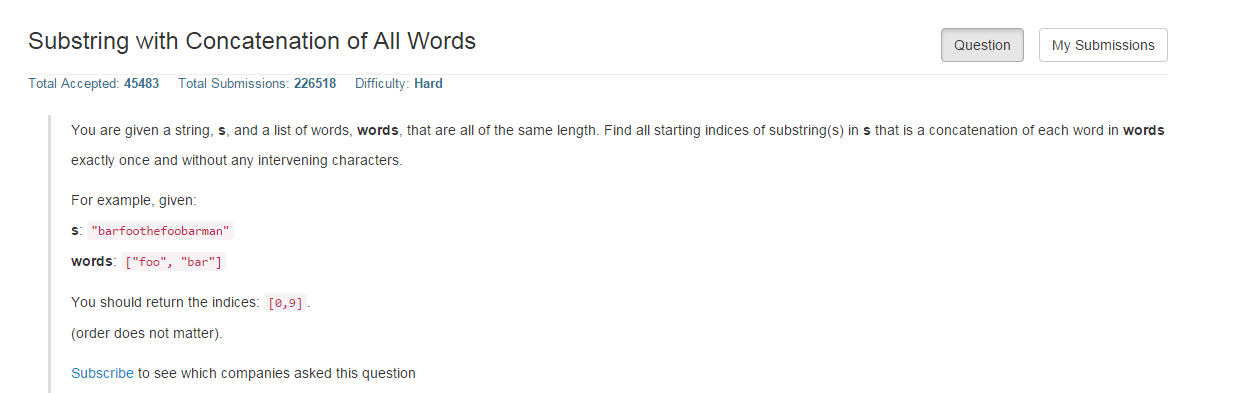
首先得弄懂题目的意思,这道题看了很久才弄明白题目意思:也就是说,给定一个字符串数组,数组中的字符串不管以什么顺序拼接在一起,得到新的字符串new,然后在s中查找new在s中第一次出现的下标,题目给的例子可以拼接成foobar或者barfoo,然后判断其起始下标分别为9,0;
按照上面说的,可以做n!次拼接,然后通过kmp算法判断在s中出现的下标,但是这种方式的效率太低,得想想其他方法,降低算法时间复杂度;
想了一会,想到了一个解决该问题的方法:依次遍历字符串s,第i(i从0开始)轮遍历时,也就是从s的s[i]开始,依次截取子字符串,截取长度为一个word的长度,然后判断words数组中是否有当前子字符串,如果没有,i++,如果存在,再从i+word.length处截取子字符串,以此类推;再判断子字符串是否存在时,可以通过一个map统计每个word出现的次数,遍历时,出现一个word,则对应次数加1,具体看代码实现:
1 class Solution { 2 public: 3 vector<int> findSubstring(string S, vector<string> &L) { 4 int l_size = L.size(); 5 6 if (l_size <= 0) { 7 return vector<int>(); 8 } 9 10 vector<int> result; 11 map<string, int> word_count; 12 int word_size = L[0].size(); 13 int i, j; 14 15 for (i = 0; i < l_size; ++i) { 16 ++word_count[L[i]]; 17 } 18 19 map<string, int> counting; 20 21 for (i = 0; i <= (int)S.length() - (l_size * word_size); ++i) { 22 counting.clear(); 23 24 for (j = 0; j < l_size; ++j) { 25 string word = S.substr(i + j * word_size, word_size); 26 27 if (word_count.find(word) != word_count.end()) { 28 ++counting[word]; 29 30 if (counting[word] > word_count[word]) { 31 break; 32 } 33 } 34 else { 35 break; 36 } 37 } 38 39 if (j == l_size) { 40 result.push_back(i); 41 } 42 } 43 44 return result; 45 } 46 };


