8、String to Integer (atoi)
题目
这道题目关键是要考虑清楚各种输入用例。针对每一种情况,函数都能处理,也就是函数鲁棒性很高。代码如下:
1 class Solution { 2 public: 3 int myAtoi(string str) { 4 int index=0; 5 int flag = 1; 6 long long res=0; 7 if(str.length()==0)return 0; 8 while (str[index]==' ')//去除空白 9 index++; 10 11 if(str[index] == '-')//负数 12 { 13 flag = -1; 14 index++; 15 } 16 else if(str[index] == '+')//负数 17 { 18 flag = 1; 19 index++; 20 } 21 int len = str.length(); 22 while (str[index]>='0'&&str[index]<='9') 23 { 24 res = res * 10 +str[index]-'0'; 25 if(res > INT_MAX) 26 return flag>0 ? INT_MAX:INT_MIN; 27 index++; 28 } 29 30 return res*flag; 31 } 32 };
----------------------------------------------------------------------------------------------分割线------------------------------------------------------------------------------------
9、Palindrome Number
题目
话不多说,直接看代码:
1 class Solution { 2 public: 3 bool isPalindrome(int x) { 4 if (x == -2147483648) 5 { 6 return false; 7 } 8 if (x<0) 9 { 10 //x=0-x; 11 return false; 12 } 13 int length = (int)log10(x*1.0)+1;//判断x的位数 14 //int s[20]; 15 int temp1 = x; 16 int temp2 = x; 17 int middle = length/2; 18 int i,j,left,right,power=length-1; 19 for (i=1;i<=middle;i++) 20 { 21 left=temp1/(int)pow(10.0,power); 22 temp1=temp1%(int)pow(10.0,power); 23 power--; 24 25 right = temp2%10; 26 temp2 = temp2/10; 27 if (left != right) 28 { 29 return false; 30 } 31 32 } 33 return true; 34 } 35 };
--------------------------------------------------------------------------------------------------分割线---------------------------------------------------------------------------
10、Regular Expression Matching
题目
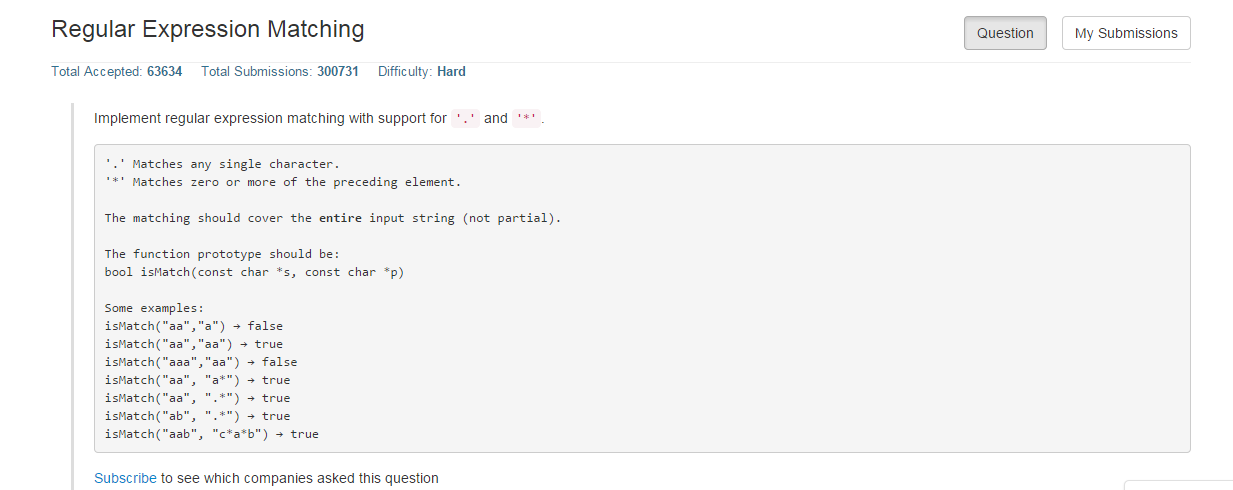
这道题目,一开始我以为要用到编译原理里面学到的自动机构造方法,后来在网上看别人的解题思路,其实可以采用递归的方法直接进行匹配,其思路是这样的;
思路1:递归。根据下一个字符是否是'*'分情况判断。
- 如果p的下一个字符不是'*',只需判断当前字符是否相等,或者p[cur]='.',递归处理s[1]和p[1];
- 如果是p的下一个'*',则当前s和p相等或者p='.'情况下,依次判断s[0...s.length]和p2]是否match;
实现代码可以参考如下:
1 class Solution { 2 public: 3 bool isMatch(string s, string p) { 4 return isMatch(s.c_str(),p.c_str()); 5 6 } 7 bool isMatch(const char *s, const char *p) { 8 // Start typing your C/C++ solution below 9 // DO NOT write int main() function 10 if (*p == 0) return *s == 0; 11 if (*(p+1) != '*') 12 { 13 if (*s != 0 && (*p == *s || *p == '.')) return isMatch(s+1, p+1); 14 else return false; 15 } 16 else 17 { 18 // *s == *p 19 while (*s != 0 && (*s == *p || *p == '.')) 20 { 21 if (isMatch(s, p+2)) return true; 22 s++; 23 } 24 return (isMatch(s, p+2)); 25 } 26 } 27 };
当然,这道题还可以采用自动机进行解决,不过难度也是很大的,需要对模式串进行分析,构造出自动机,然后通过s串逐个字符的匹配。下面是最开始未完成的代码:

1 class node 2 { 3 public: 4 node() 5 { 6 val = 0; 7 self = -1; 8 isEnd = false; 9 10 } 11 node(char c) 12 { 13 val = c; 14 self = -1; 15 isEnd = false; 16 } 17 18 public: 19 char val; 20 int self;//是否包含* 21 bool isEnd;//是否是终态 22 23 24 }; 25 26 27 class Solution { 28 public: 29 bool isMatch(string s, string p) 30 { 31 if("" == s) 32 return true; 33 if("" == p) 34 return false; 35 vector<node*> status;//存储自动机状态节点 36 node *temp; 37 38 temp = new node(p[0]); 39 status.push_back(temp); 40 41 int i=1; 42 int index = 0; 43 while (p[i] != '\0')//注意,如果模式是a*aaa最终转换为节点为{a,3,true},true表示当前节点是终态 44 { 45 index = status.size(); 46 if(p[i] == '*') 47 { 48 if(status[index-1]->self != -1)//考虑模式中有a*a*这种情况,当处理第二个*时,前一个节点的self不为-1 49 status[index-1]->self = 0; 50 else 51 status[index-1]->self++; 52 i++; 53 continue; 54 } 55 if(p[i] == status[index-1]->val) 56 { 57 status[index-1]->self++; 58 i++; 59 continue; 60 } 61 temp = new node(p[i]); 62 status.push_back(temp); 63 64 i++; 65 66 } 67 index = status.size(); 68 index--; 69 //比如a*b*最后做出的两个节点都是终态 70 status[index]->isEnd = true;//最后一个节点肯定是终态 71 72 while (index >= 0)//判断各个节点是不是终态 73 { 74 if(status[index]->self != -1) 75 status[index]->isEnd = true; 76 else//只要当前不是终态,那它之前的所有节点都不是终态 77 { 78 break; 79 } 80 index--; 81 } 82 83 i=0; 84 index = 0; 85 int nodeCount = status.size(); 86 87 while(s[i] != '\0') 88 { 89 if(index >= nodeCount) 90 return false; 91 if(status[index]->val == '.') 92 { 93 if(status[index]->self != -1) 94 { 95 if(status[index]->isEnd) 96 return true; 97 else 98 { 99 100 } 101 } 102 else 103 { 104 i++; 105 index++; 106 continue; 107 } 108 } 109 else 110 { 111 112 } 113 i++; 114 } 115 116 } 117 };
---------------------------------------------------------------------------------------------------分割线--------------------------------------------------------------------------
11、Container With Most Water
题目
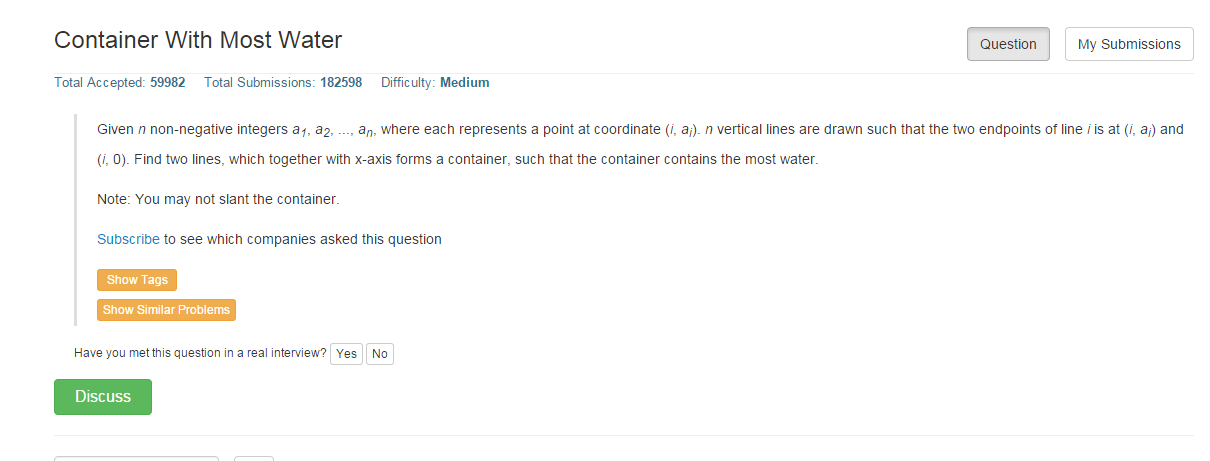
题目要求:给定n个非负整数,构成n个点,其点坐标为(i,ai),然后过每个点做x轴的垂线,形成n条线段,任意选择两条垂线段作为“容器”,求最大容器的所能容下的水量。
这类求最值的问题,第一想法都是暴利,也就是一次遍历两两线段,求其容器体积,并找出最大值,其代码如下:
1 class Solution { 2 public: 3 int maxArea(vector<int>& height) { 4 5 int count = height.size(); 6 int i,j; 7 int volumn = 0,temp; 8 for (i = 0;i < count;i++) 9 { 10 for(j = i+1;j < count;j++) 11 { 12 temp = height[i] > height [j] ? height[j] : height[i];//取最小值,也就是边矮的 13 14 if(volumn < temp * (j-i)) 15 volumn = temp * (j-i); 16 } 17 } 18 19 return volumn; 20 21 } 22 };
很显然,这中思路的时间复杂度肯定是O(n*n);
仔细一想,这个题目可以采用首尾夹逼的策略进行求解,其代码如下:
1 class Solution { 2 public: 3 int maxArea(vector<int> &height) { 4 // Start typing your C/C++ solution below 5 // DO NOT write int main() function 6 int i = 0; 7 int j = height.size() - 1; 8 9 int ret = 0; 10 while(i < j) 11 { 12 int area = (j - i) * min(height[i], height[j]); 13 ret = max(ret, area); 14 15 if (height[i] <= height[j]) 16 i++; 17 else 18 j--; 19 } 20 21 return ret; 22 } 23 };



