[AHOI2005][洛谷 P2054] SHUFFLE 洗牌

这是一道逆元的模板题。

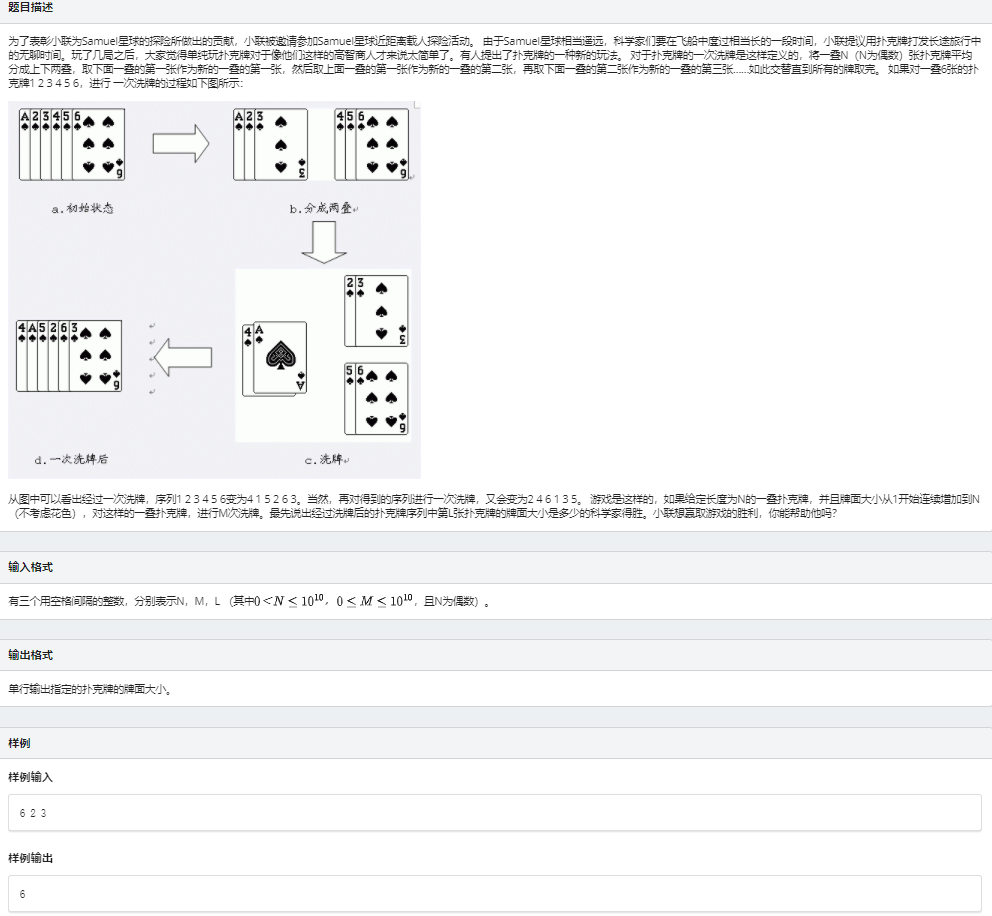
看到题，首先找下规律：

首先想到是否存在循环，即经过多次洗牌后回到原状态的情况，但手玩了几组以后发现有循环但没有规律，只能知道循环节长度小于等于 \(n\) ，显然会 \(TLE\) ；
所以对于一些循环节较长的数据很容易被卡掉 （比如这组：9000000000 1 1）
代码转载自 @Ishar-zdl

找循环节

#include<bits/stdc++.h>
#define int long long
using namespace std;
main(){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int n;cin>>n;int m,l;cin>>m>>l;
    int c=l,f=0;
    for(int i=1;i<=n;i++){
        l=(l+1)/2+(l%2)*n/2;
        if(l==c){f=i;break;}
    }
    f=m%f;
    for(int i=1;i<=f;i++)
    l=(l+1)/2+(l%2)*n/2;
    cout<<l;
}

然后自己推一下样例：
（以下每一行代表一次洗牌）

第一张	第二张	第三张	第四张	第五张	第六张
1	2	3	4	5	6
4	1	5	2	6	3
2	4	6	1	3	5
1	2	3	4	5	6

对 \(1\) 这张牌来说，位置变化是 \(1\) → \(2\) → \(4\) → \(1\)
\(1\) → \(2\) → \(4\) 可以很明显看出是 \(\times \ 2\) 的变化
那 \(4\) → \(1\) 呢 ？
可以发现 \(1\) \(=\) \(4\) \(\times\) \(2\) \(-\) \(7\),也就是 \(1\) \(=\) \(4\) \(\times\) \(2\) \(mod\) \(7\)
所以得出结论：第 \(i\) 张牌最后的位置就是 \(i\) \(\times\) \(2^m\) \(mod\) \((n+1)\) 。

那么对于洗完牌后的第 \(l\) 张牌来说，它最初的位置就是 \(l\) \(\div\) \(2^m\) \(mod\) \((n+1)\) ;
所以我们只要求出 \(2^m\) 在 \(mod \ (n+1)\) 意义下的逆元即可。

于是打出代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m,l,x55,y55,x,y;
ll exgcd(ll a,ll b,ll &x,ll &y){
	if(b==0){
		x=1;
		y=0;
		return a;
	}
	ll ret=exgcd(b,a%b,x,y);
	ll tmp=x;
	x=y;
	y=tmp-a/b*y;
	return ret;
}
ll qp(ll b,ll p,ll k){
	ll ans=1;
	b=b%k;
	while(p>0){
		if(p&1)ans=(ans*b)%k;
		p=p>>1;
		b=(b*b)%k;
	}
	return ans;
}
int main(){
	cin>>n>>m>>l;
	ll mod=n+1;
	ll t=qp(2,m,mod);
	exgcd(t,mod,x,y);
	x=(x%mod+mod)%mod;
	l=(l*x)%mod;
	cout<<l;
	return 0;
}

但是

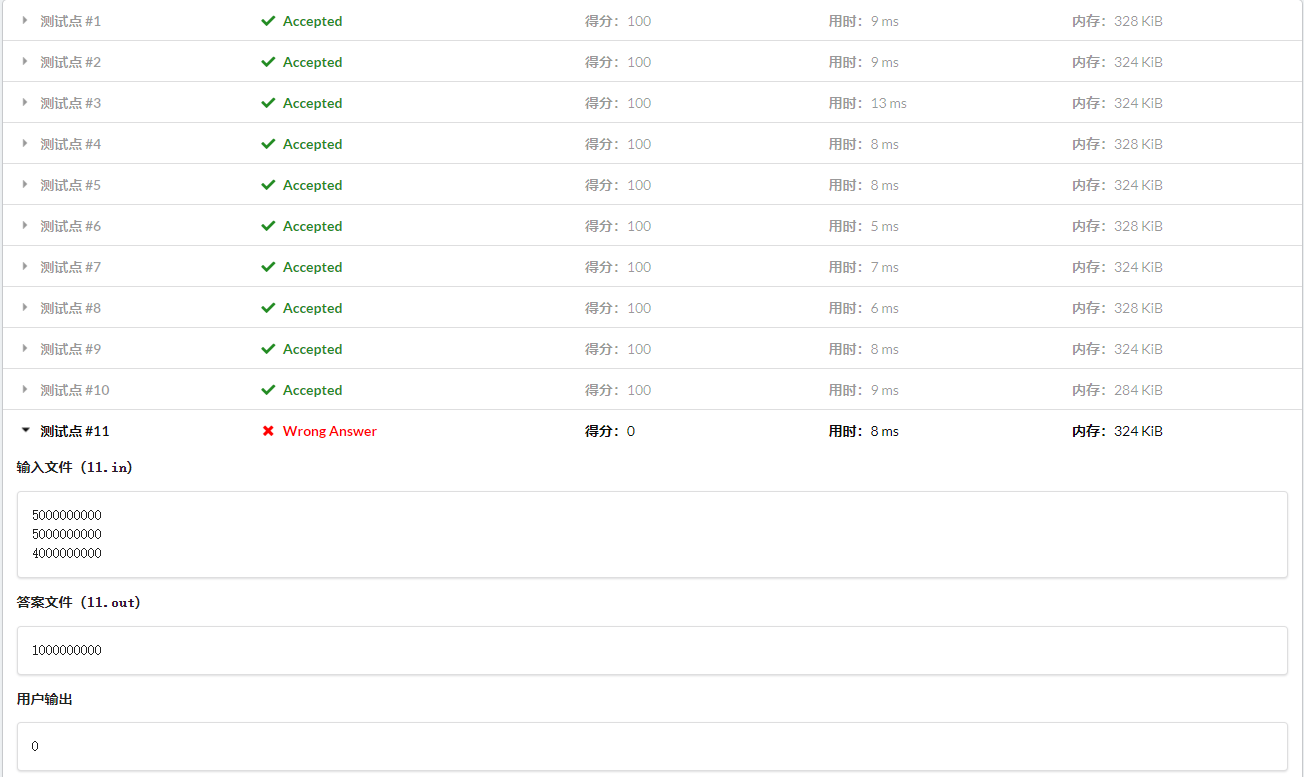
又有人加测试点

简单思考一下可以发现，对于 \(1e10\) 的数据，快速幂中的 \(b \times b\) 在极限情况下可以达到 \(1e20\) ， 是 \(long\) \(long\) 无法承受的 ；

那怎么办？

long long 不够用？__int128 拯救你!

__int128 可以，但这里要介绍的是另一种方法：

龟速乘！

也就是边乘边模，通过牺牲一些时间来避免乘法炸 \(long\) \(long\) 的方式，与快速幂很像

龟速乘

ll mul(ll b,ll p,ll k){//龟速乘
	ll ans=0;
	b=b%k;
	while(p>0){
		if(p&1)ans=(ans+b)%k;
		p>>=1;
		b=(b+b)%k;
	}
	return ans%k;
}

可以与快速幂对比记忆

ll qp(ll b,ll p,ll k){//快速幂
	ll ans=1;
	b=b%k;
	while(p>0){
		if(p&1)ans=(ans*b)%k;
		p=p>>1;
		b=(b*b)%k;
	}
	return ans;
}

所以改一改就可以过了。

完整代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m,l,x,y;
ll exgcd(ll a,ll b,ll &x,ll &y){//扩展欧几里得求逆元，因为这题的模数 n+1 不一定是质数，但一定是奇数，即与 2^m 互质
	if(b==0){
		x=1;
		y=0;
		return a;
	}
	ll ret=exgcd(b,a%b,x,y);
	ll tmp=x;
	x=y;
	y=tmp-a/b*y;
	return ret;
}
ll mul(ll b,ll p,ll k){//龟速乘
	ll ans=0;
	b=b%k;
	while(p>0){
		if(p&1)ans=(ans+b)%k;
		p>>=1;
		b=(b+b)%k;
	}
	return ans%k;
}
ll qp(ll b,ll p,ll k){//快速幂
	ll ans=1;
	b=b%k;
	while(p>0){
		if(p&1)ans=mul(ans,b,k);//记得把这里改为龟速乘
		p>>=1;
		b=mul(b,b,k);//还有这里
	}
	return ans%k;
}
int main(){
	cin>>n>>m>>l;
	ll mod=n+1;
	ll t=qp(2,m,mod);// 2^m
	exgcd(t,mod,x,y);// 2^m 的逆元
	x=(x%mod+mod)%mod;
	l=mul(x,l,mod);//龟速乘
	cout<<l;
	return 0;
}