[NOI2010][洛谷P2048] 超级钢琴

一道很不错也很难的 ST表
Debug 了好久之后发现撞变量了 😦

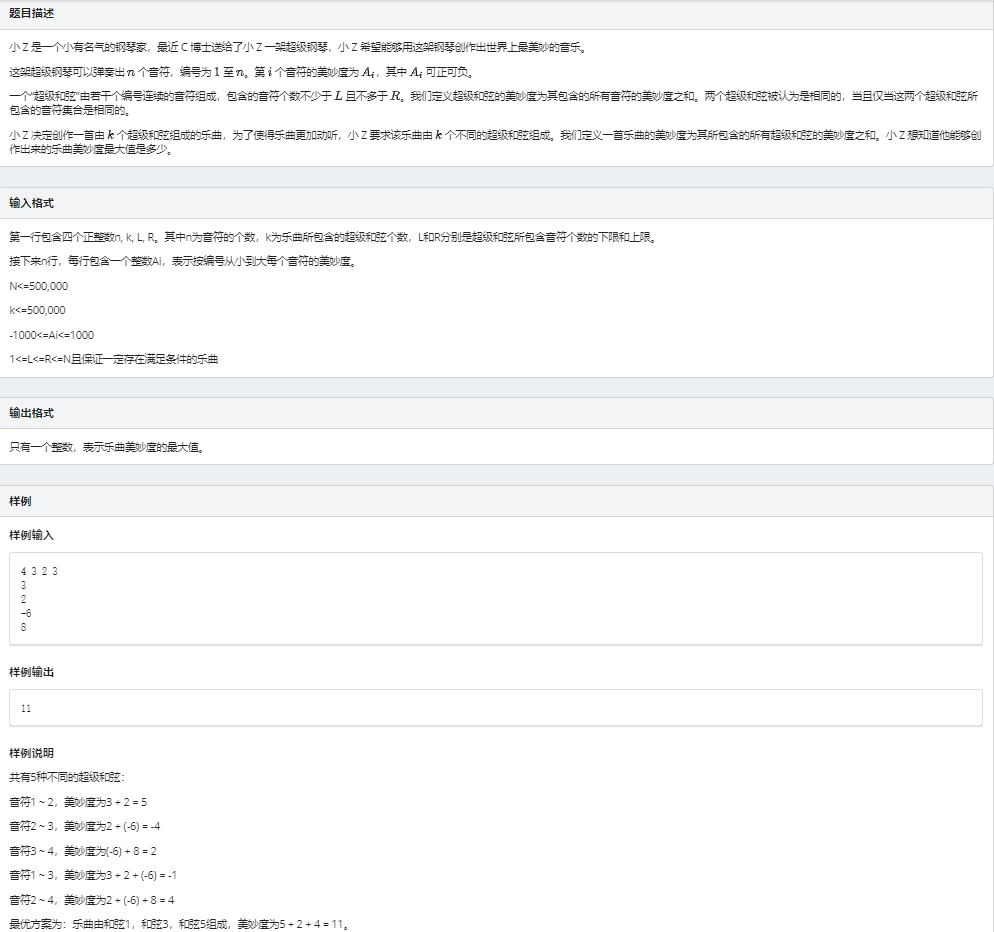
一、题意

给出一个数组 \(a[i]\) ，找出其中前 \(k\) 大的 长度介于 \(l\) 和 \(r\) 之间的 子段和

二、暴力

首先考虑暴力枚举每个长度，求出总和后扔到一个优先队列中，最后取出堆顶的 \(k\) 个元素求和
期望得分：\(20\) 原因：\(TLE\)
实际得分：\(30\) 原因：\(MLE\)
还来不及超时就被内存卡掉了

暴力

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int n,k,l,r,a[N];
priority_queue<int> q;
int main(){
	cin>>n>>k>>l>>r;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		a[i]+=a[i-1];
	}
	
	for(int i=l;i<=r;i++){
		for(int j=1;j+i-1<=n;j++){
			q.push(a[j+i-1]-a[j-1]);
		}
	}
	
	int ans=0;
	for(int i=1;i<=k;i++){
		ans+=q.top();
		q.pop();
	}
	cout<<ans;
	return 0;
}

三、优化

首先对于区间和，肯定是要用前缀和优化

对于区间的求解，我们可以先不求出所有的可能，而是先将一些最优解放入堆中，再在取出后放入它的次优解来更新

对于每一个区间，先固定左端点 \(l\) ，放入其向右的最优解，用一个四元组 \([x,y,l,r]\)来表示：

其中，\(x\) 表示左端点，\(y\) 表示当前的右端点，\(l\) 和 \(r\) 表示右端点的范围；

求解当前区间最优解则可以用ST表解决；

将全部最优解放入后，从堆中取出最优解，更新 \(ans\) ，并向堆中放入新的四元组 \([x,query(l,y-1),l,y-1]\) 和 \([x,query(y+1,r),y+1,r]\) ，即区间 \([l,r]\) 去除 \(y\) 后的最优解，记得判断 \(l\) 与 \(r\) 是否等于 \(t\) ;

重复该操作 \(k\) 次后得到的结果即为答案。

完整代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e5+5;
int n,m,l,r;
ll c[N];//前缀和数组 要开long long 
struct node{
	int x,y,l,r;
	bool operator < (const node &a)const{
		return c[y]-c[x-1]<c[a.y]-c[a.x-1];//重载，将较大的区间放在上面 
	}
}; 
priority_queue<node> q;
int f[N][30];//ST数组 
ll ans;//开 long long !
int query(int l,int r){//查询最优解 返回的是位置 
	int k=log2(r-l+1);
	if(c[f[l][k]]>c[f[r-(1<<k)+1][k]])return f[l][k];
	else return f[r-(1<<k)+1][k];
}
main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n>>m>>l>>r;//m 就是原题中的 k  
	//打的时候和下面的 k=log2(n) 撞了 :( 遂改 
	for(int i=1;i<=n;i++){
		cin>>c[i];
		c[i]+=c[i-1];
		f[i][0]=i;
	}//初始化 
	int k=log2(n);
	for(int j=1;j<=k;j++){
		for(int i=1;i+(1<<j)-1<=n;i++){
			if(c[f[i][j-1]]>c[f[i+(1<<(j-1))][j-1]])f[i][j]=f[i][j-1];
			else f[i][j]=f[i+(1<<(j-1))][j-1];//寻找最优 
			
		}
	}
	for(int i=1;i+l-1<=n;i++){//push 
		q.push({i,query(i+l-1,min(n,i+r-1)),i+l-1,min(n,i+r-1)});
	}	
	for(int i=1;i<=m;i++){//寻找次优解 
		node tmp=q.top();
		q.pop();
		int x=tmp.x,y=tmp.y,l=tmp.l,r=tmp.r;
		ans+=c[y]-c[x-1];
		if(l!=y)q.push({x,query(l,y-1),l,y-1});
		if(r!=y)q.push({x,query(y+1,r),y+1,r});
	}
	cout<<ans;//输出 
	return 0;
}