[SCOI2011][洛谷P3275] 糖果
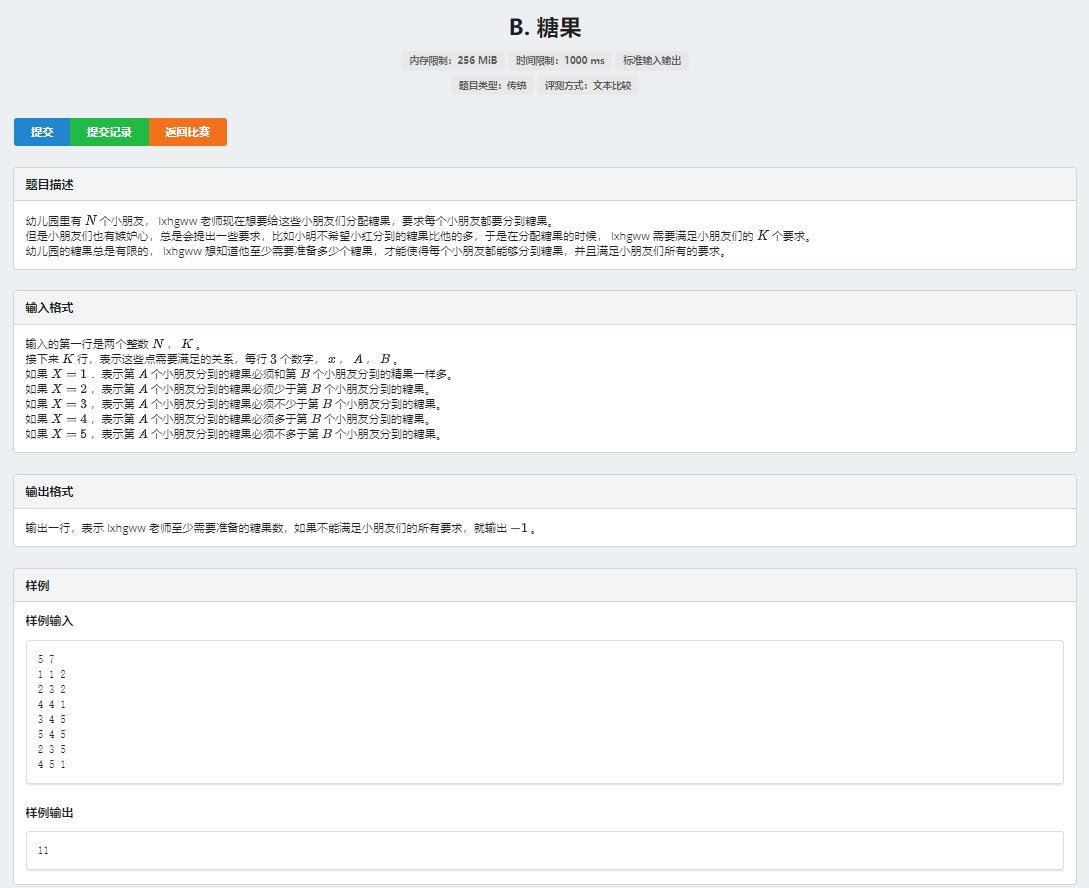
本来这是一道差分约束板子题/水题
SPFA-BFS和SPFA-DFS都能过
BFS
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=100005;
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
struct edge{
int to,next,w;
}e[N*1000];
int cnt;
int h[N];
void add(int u,int v,int w){
e[++cnt].w=w;
e[cnt].to=v;
e[cnt].next=h[u];
h[u]=cnt;
}
int dis[N];
int sum[N];
bool vis[N];
int n,m;
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
int s;
int a,b;
cin>>s>>a>>b;
switch(s){
case(1):add(a,b,0);add(b,a,0);break;
case(2):
if(a==b){
cout<<-1;
exit(0);
}
add(a,b,1);
break;
case(3):add(b,a,0);break;
case(4):
if(a==b){
cout<<-1;
exit(0);
}
add(b,a,1);
break;
case(5):add(a,b,0);break;
}
}
for(int i=1;i<=n;i++){
add(0,i,1);
}
vis[0]=1;
queue<int> q;
q.push(0);
while(!q.empty()){
int u=q.front();
q.pop();
vis[u]=0;
sum[u]++;
if(sum[u]>=n){
cout<<-1;
exit(0);
}
for(int i=h[u];i;i=e[i].next){
int to=e[i].to;
if(dis[to]<dis[u]+e[i].w){
dis[to]=dis[u]+e[i].w;
if(!vis[to]){
vis[to]=1;
q.push(to);
}
}
}
}
ll ans=0;
for(int i=1;i<=n;i++){
ans+=dis[i];
}
cout<<ans;
}
DFS
#include<bits/stdc++.h>
using namespace std ;
#define mk make_pair
#define pb push_back
long long n,m,dis[100005],sum,cnt[100005];
queue<long long >q;
bool v[100005];
vector<pair<long long,long long> >ba[100005];
void spfa(long long x){
v[x]=1;
for(auto i:ba[x]){
if(dis[i.first]<dis[x]+i.second){
dis[i.first]=dis[x]+i.second;
if(v[i.first]){
cout<<-1;
exit(0);
}
spfa(i.first);
}
}
v[x]=0;
}
int main(){
cin>>n>>m;
long long x,A,B;
for(long long i=1;i<=m;i++){
scanf("%lld%lld%lld",&x,&A,&B);
if(x==1)ba[A].pb(mk(B,0)),ba[B].pb(mk(A,0));
else if(x==2)ba[A].pb(mk(B,1));
else if(x==3)ba[B].pb(mk(A,0));
else if(x==4)ba[B].pb(mk(A,1));
else ba[A].pb(mk(B,0));
}
memset(dis,0xcf,sizeof(dis));
memset(v,0,sizeof(v));
for(long long i=1;i<=n;i++)ba[0].pb(mk(i,1));
dis[0]=0;
spfa(0);
for(long long i=1;i<=n;i++){
// cout<<dis[i]<<" ";
sum+=dis[i];
}
cout<<sum;
}
然后某些人向学校题库中加了一些洛谷的测试点
于是
简直罪大恶极
所以,这道题的正解其实是 差分约束建图 + tarjan缩点 + 拓扑排序 + dp更新答案
一、差分约束
这部分就是正常的差分约束.
根据题意,小朋友的嫉妒一共有 \(5\) 种情况:
如果 X=1, 表示第 A 个小朋友分到的糖果必须和第 B 个小朋友分到的糖果一样多;
如果 X=2, 表示第 A 个小朋友分到的糖果必须少于第 B 个小朋友分到的糖果;
如果 X=3, 表示第 A 个小朋友分到的糖果必须不少于第 B 个小朋友分到的糖果;
如果 X=4, 表示第 A 个小朋友分到的糖果必须多于第 B 个小朋友分到的糖果;
如果 X=5, 表示第 A 个小朋友分到的糖果必须不多于第 B 个小朋友分到的糖果;
题目要求我们输出最少的糖果数量,那么:
当 \(X\) = \(1\) 、 \(3\) 、 \(5\) 时,显然令两个小朋友的糖果数量相同最优
当 \(X\) = \(2\) 、 \(4\) 时,两个小朋友的糖果数量相差 \(1\) 最优
所以对于 \(X\) = \(1\) 、 \(3\) 、 \(5\),我们建一条边权为 \(0\) 的边;对于\(X\) = \(2\) 、 \(4\),建一条边权为 \(1\) 的边
注意:\(X\) = \(1\) 时 \(A\) = \(B\) 要建双向边!
这样之后就可以用 tarjan 将这两个点缩为一个点,满足之后拓扑排序时的无环要求
建图
for(int i=1;i<=m;i++){//略有修改,m为原题中的k,即边数
op=read();x=read();y=read();
switch(op){
case 1:
e1[x].push_back({y,0});//e1 为原图,存的是结构体node,第一个为终点,第二个为操作(1~5)
e1[y].push_back({x,0});
break;
case 2:
e1[x].push_back({y,1});
break;
case 3:
e1[y].push_back({x,0});
break;
case 4:
e1[y].push_back({x,1});
break;
default:
e1[x].push_back({y,0});
}
}
二、tarjan
没什么好说的,正常 tarjan 缩点,将糖果数量可以相等的点缩为一个点,记得记录所属的强联通分量和其大小即可
缩完点后建新图连边,同时判断是否存在无解情况,即对于两个在不同强连通分量中的点,它们的糖果数量应相等的情况
tarjan
void tarjan(int x){
dfn[x]=low[x]=++num;
vis[x]=1;
s.push(x);
for(auto &i:e1[x]){//auto
/*相当于:
for(int i=0;i<e1[x].size();i++){
int nx=e1[x][i].next;
*/
int nx=i.next;
if(!dfn[nx]){
tarjan(nx);
low[x]=min(low[x],low[nx]);
}
else if(vis[nx]==1){
low[x]=min(low[x],dfn[nx]);
}
}
if(dfn[x]==low[x]){
int y;
cnt++;
do{
y=s.top();
s.pop();
id[y]=cnt;//记录所属强联通分量
size[cnt]++;//更新大小
vis[y]=0;
}while(x!=y);
}
}
建新图
for(int i=1;i<=n;i++){
for(auto &j:e1[i]){
int nx=j.next;
x=id[i],y=id[nx];
if(x==y&&j.w==1){
cout<<-1;//判断无解情况
return 0;
}
if(x!=y){
e2[x].push_back({y,j.w});
in[y]++;//统计入度,拓扑排序会用到
}
}
}
三、拓扑排序 & dp求解
在建好的新图上跑一遍拓扑排序,同时用dp更新最少糖果数量
拓扑排序 + 统计答案
queue<int> q;
for(int i=1;i<=cnt;i++){//拓扑排序与dp初始化
if(!in[i]){
q.push(i);
f[i]=1;//f数组即dp数组
}
}
while(!q.empty()){//拓扑排序
int u=q.front();
q.pop();
for(auto &i:e2[u]){
int nx=i.next;
in[nx]--;
f[nx]=max(f[nx],f[u]+i.w);//更新当前点所需最少糖果
if(!in[nx])q.push(nx);
}
}
for(int i=1;i<=cnt;i++){
ans+=(ll)f[i]*size[i];//更新ans,加上当前 这个强连通分量所需最少糖果 * 强连通分量大小 记得开long long
}
cout<<ans;
四、完整代码
记得开 long long !
完整代码(纯享版)
#include<bits/stdc++.h>
#include<vector>
using namespace std;
typedef long long ll;
const int N=1e6+5;
int n,m,op,x,y;
int dfn[N],low[N],num,cnt,size[N],id[N];
int f[N],in[N];
ll ans;
struct node{
int next,w;
};
vector<node> e1[N],e2[N];
bool vis[N];
stack<int> s;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return x*f;
}
void tarjan(int x){
dfn[x]=low[x]=++num;
vis[x]=1;
s.push(x);
for(auto &i:e1[x]){
int nx=i.next;
if(!dfn[nx]){
tarjan(nx);
low[x]=min(low[x],low[nx]);
}
else if(vis[nx]==1){
low[x]=min(low[x],dfn[nx]);
}
}
if(dfn[x]==low[x]){
int y;
cnt++;
do{
y=s.top();
s.pop();
id[y]=cnt;
size[cnt]++;
vis[y]=0;
}while(x!=y);
}
}
int main(){
n=read();m=read();
for(int i=1;i<=m;i++){
op=read();x=read();y=read();
switch(op){
case 1:
e1[x].push_back({y,0});
e1[y].push_back({x,0});
break;
case 2:
e1[x].push_back({y,1});
break;
case 3:
e1[y].push_back({x,0});
break;
case 4:
e1[y].push_back({x,1});
break;
default:
e1[x].push_back({y,0});
}
}
for(int i=1;i<=n;i++){
if(!dfn[i])tarjan(i);
}
for(int i=1;i<=n;i++){
for(auto &j:e1[i]){
int nx=j.next;
x=id[i],y=id[nx];
if(x==y&&j.w==1){
cout<<-1;
return 0;
}
if(x!=y){
e2[x].push_back({y,j.w});
in[y]++;
}
}
}
queue<int> q;
for(int i=1;i<=cnt;i++){
if(!in[i]){
q.push(i);
f[i]=1;
}
}
while(!q.empty()){
int u=q.front();
q.pop();
for(auto &i:e2[u]){
int nx=i.next;
in[nx]--;
f[nx]=max(f[nx],f[u]+i.w);
if(!in[nx])q.push(nx);
}
}
for(int i=1;i<=cnt;i++){
ans+=(ll)f[i]*size[i];
}
cout<<ans;
return 0;
}
附上洛谷大佬 @kangli 的迭代贪心法 代码:
虽然也被卡了
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
struct candy{
int X,A,B;
}q[101010];
int n,k;
int a[101010];
int main()
{
cin>>n>>k;
for (int i=1; i<=k; i++){
scanf("%d%d%d",&q[i].X,&q[i].A,&q[i].B);
}
for (int i=1; i<=n; i++) a[i]=1;
for (int T=1; T<=200; T++){
for (int i=1; i<=k; i++){
if (q[i].X==1) {
if (a[q[i].A]>a[q[i].B]) a[q[i].B]=a[q[i].A];
else a[q[i].A]=a[q[i].B];
}
else if (q[i].X==2){
if (a[q[i].A]>=a[q[i].B]) a[q[i].B]=a[q[i].A]+1;
}
else if (q[i].X==3){
if (a[q[i].A]<a[q[i].B]) a[q[i].A]=a[q[i].B];
}
else if (q[i].X==4){
if (a[q[i].A]<=a[q[i].B]) a[q[i].A]=a[q[i].B]+1;
}
else if (q[i].X==5){
if (a[q[i].A]>a[q[i].B]) a[q[i].B]=a[q[i].A];
}
}
}
for (int i=1; i<=k; i++){
if (q[i].X==1) {
if (a[q[i].A]>a[q[i].B]) {cout<<"-1";return 0;}
}
else if (q[i].X==2){
if (a[q[i].A]>=a[q[i].B]) {cout<<"-1";return 0;}
}
else if (q[i].X==3){
if (a[q[i].A]<a[q[i].B]) {cout<<"-1";return 0;}
}
else if (q[i].X==4){
if (a[q[i].A]<=a[q[i].B]) {cout<<"-1";return 0;}
}
else if (q[i].X==5){
if (a[q[i].A]>a[q[i].B]) {cout<<"-1";return 0;}
}
}
long long ans=0;
for (int i=1; i<=n; i++) ans+=a[i];
cout<<ans<<endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号