[POI2010][BZOI2086][洛谷P3503] Blocks

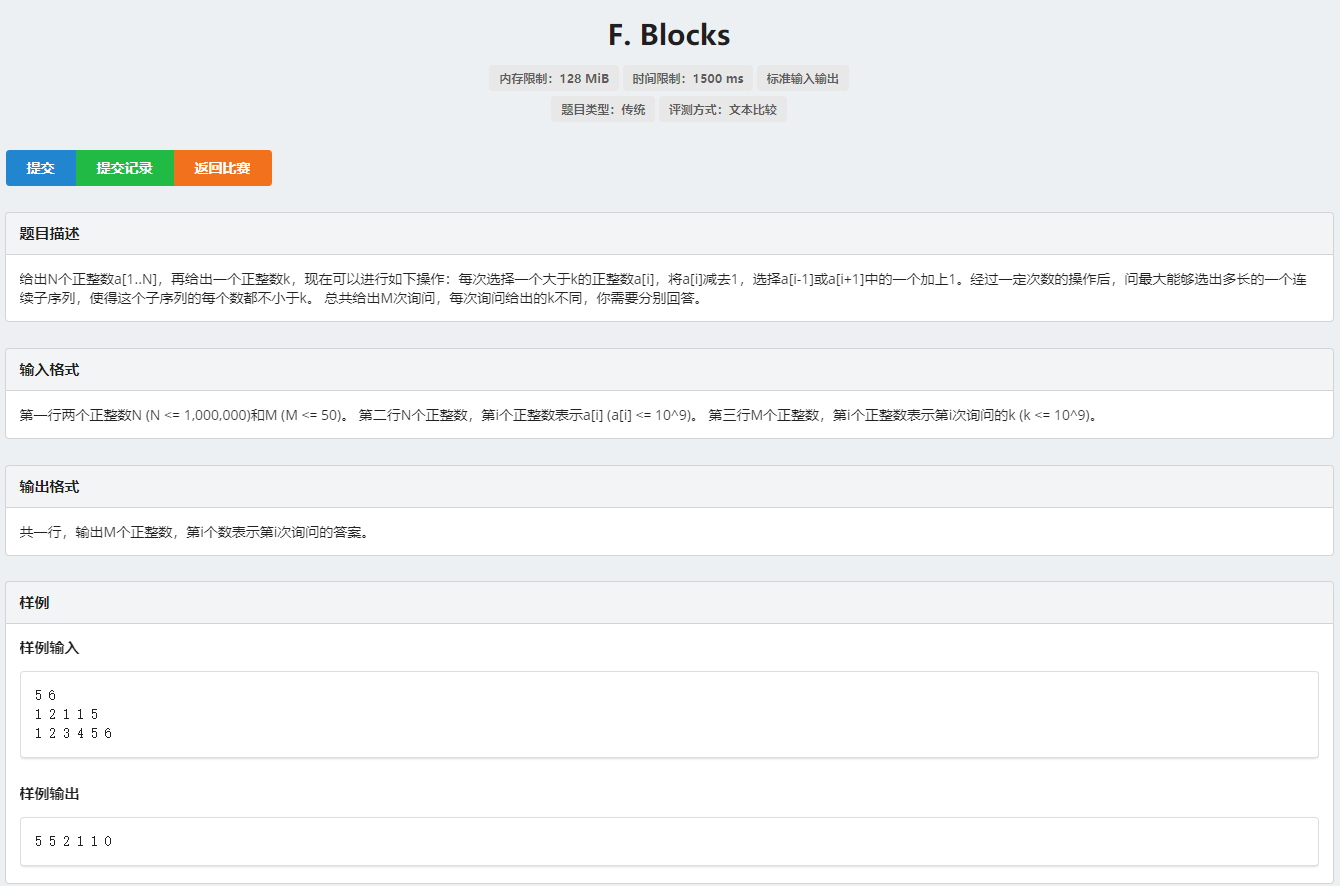
先看数据范围，n ≤ 1e7，k ≤ 1e9，暴力显然行不通，只能考虑单调栈；
首先题目中说每一个数都要大于 k ，那么我们可以在初始化时就将每一个数都减去 k ，将问题转化为从正数中取出数加到负数里；
然后维护一个前缀和，来判断一个区间是否符合要求；显然，当sum[j]-sum[i] ≥ 0时，区间[i+1,j]符合题意，长度为 j-i;
所以，到这一步，其实上是求出 满足 sum[j]-sum[i] ≥ 0 时 j-i 的最大值。

初始化

s.clear();//将栈清空，我用的是手写栈，STL栈可以使用 while(!s.empty())s.pop() 的方式实现
scanf("%lld",&k);
for(int i=1;i<=n;i++){
	sum[i]=sum[i-1]+a[i]-k;
}

接下来，考虑实现方式；
我们发现，如果 i ≤ j && sum[i] ≤ sum[j] , 那么明显以 i 作为区间的左端点比 j 更优；
所以维护单调栈时，只有 sum[i] ≤ sum[s.top()] 时才能够将其压入栈中，所以这是一个单调递减栈；
因为我们是从1~n找出的单调栈，而我们要寻找最大区间，所以在寻找最左边界时，要从n倒着遍历；
当当前元素的前缀和大于等于栈顶元素的前缀和，即 sum[i] ≥ sum[s.top()] 时，就得到了一组合法解，然后将其pop掉；
而当 sum[i] < sum[s.top()] 时，由于栈中元素是单调递减的，当前解不合法，栈中其它的解也就更不合法了，不用再去考虑；
最后更新ans值即可。
另外：要开long long，因为有前缀和

完整代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e7+5;
const int inf=0x7fffffff;
ll n,a[N],tmp[N],sum[N],m,k,maxn=-inf;//十年OI一场空，不开long long见祖宗
struct Stack{//手写栈，基本操作和STL栈一样，只多一个clear()
	int stk[N];
	int tp;
	void clear(){tp=0;}
	int top(){return stk[tp];}
	void push(int x){stk[++tp]=x;}
	void pop(){tp--;}
	bool empty(){return tp==0;}
	int size(){return tp;}
}s;
int main(){
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%lld",&a[i]);
	}
	while(m--){
		s.clear();
		scanf("%lld",&k);
		for(int i=1;i<=n;i++){
			sum[i]=sum[i-1]+a[i]-k;//求前缀和，直接减去k
		}
		ll ans=0;
		s.push(0);
		for(int i=1;i<=n;i++)if(sum[s.top()]>=sum[i])s.push(i);//正序搜索，压栈
		for(ll i=n;i>=1;i--){//倒序搜索，寻找合法区间
			ll tmp;
			while(!s.empty()&&sum[s.top()]<=sum[i]){
				tmp=s.top();//区间合法，更新tmp
				s.pop();//栈顶元素退栈
			}
			ans=max(ans,i-tmp);//更新ans的值
		}
		printf("%lld ",ans);
	}
	return 0;
}