[COGS 755] 山海经
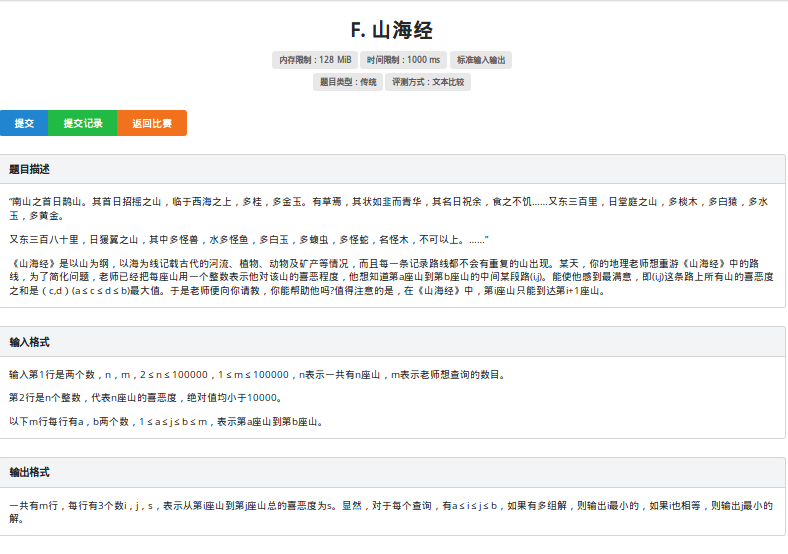
这是一道美妙的线段树板子,能够有效地提升我们的读题,理解,思考和代码能力;
综上,这是一道大模拟
显然,对于这道题的数据范围,直接暴力是行不通的,只能拿30分:
30分暴力
#include<bits/stdc++.h>
using namespace std;
const int N=1000005;
const int inf=0x7fffffff;
struct tree{
int l,r,maxn,minn,sum,lazy;
}t[N<<2];
int a[N],n,m;
string ask;
int x,y;
void update(int x){
t[x].sum=t[x<<1].sum+t[x<<1|1].sum;
t[x].maxn=max(t[x<<1].maxn,t[x<<1|1].maxn);
t[x].minn=min(t[x<<1].minn,t[x<<1|1].minn);
}
void build(int k,int l,int r){
t[k].l=l;
t[k].r=r;
if(l==r){
t[k].maxn=t[k].sum=t[k].minn=a[l];
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
update(k);
}
void add(int k,int p,int val){
int l=t[k].l,r=t[k].r;
if(l==r){
t[k].sum+=val;
t[k].maxn=val;
return;
}
int mid=(l+r)>>1;
if(p<=mid)add(k<<1,p,val);
else add(k<<1|1,p,val);
update(k);
}
int getsum(int k,int l,int r){
int kl=t[k].l,kr=t[k].r;
if(l<=kl&&kr<=r){
return t[k].sum;
}
int mid=(kl+kr)>>1;
int res=0;
if(l<=mid)res+=getsum(k<<1,l,r);
if(r>mid)res+=getsum(k<<1|1,l,r);
return res;
}
int getmax(int k,int l,int r){
int kl=t[k].l,kr=t[k].r;
if(l<=kl&&kr<=r){
return t[k].maxn;
}
int mid=(kl+kr)>>1;
int res=-inf;
if(l<=mid)res=max(res,getmax(k<<1,l,r));
if(r>mid)res=max(res,getmax(k<<1|1,l,r));
return res;
}
int getmin(int k,int l,int r){
int kl=t[k].l,kr=t[k].r;
if(l<=kl&&kr<=r){
return t[k].minn;
}
int mid=(kl+kr)>>1;
int res=inf;
if(l<=mid)res=min(res,getmin(k<<1,l,r));
if(r>mid)res=min(res,getmin(k<<1|1,l,r));
return res;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
build(1,1,n);
while(m--){
cin>>x>>y;
int ans=-inf,ii,jj;
for(int i=x;i<=y;i++){
for(int j=i;j<=y;j++){
if(getsum(1,i,j)>ans){
ans=getsum(1,i,j);
ii=i;jj=j;
}
}
}
cout<<ii<<" "<<jj<<" "<<ans<<endl;
}
return 0;
}
所以,我们就需要去维护一下最大子区间。
对于一个子区间,它与原区间的关系有以下三种:
left---l 子区间1 l------mid----------------right
left--------------------mid--l 子区间2 l----right
left----------l 子区间3 mid l----------------right
前两种情况简单,可以直接由子区间转移而来;
而对于第三种,我们可以将其从 mid 处分割成两个区间,将其转化为左子区间的最大后缀和 + 右子区间的最大前缀和;
所以我们还要多维护两个变量。
并且,由于要输出路径,所以我们还要维护四个变量,即:
取到左子区间的最大后缀和时的左节点编号;
取到右子区间的最大前缀和时的右节点编号;
取到最大值时的两端节点编号。
总计十个变量:
struct tree{
int l,r;//维护区间的左右端点
int sum;//区间的满意值之和
int lmax,rleft;//最大左子区间后缀和及取到时左节点编号
int rmax,lright;//最大右子区间前缀和及取到时右节点编号
int maxn,mleft,mright;//最大子区间的满意值之和,左端点,右端点
}t[N<<2];
初始化
void build(int k,int l,int r){
t[k].l=l;
t[k].r=r;
if(l==r){
t[k]={l,r,a[l],a[l],l,a[l],l,a[l],l,l};
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
pushup(k);
}
Pushup 函数
void pushup(int k){
t[k].sum=t[k<<1].sum+t[k<<1|1].sum;//更改区间和
int sum1=0,sum2=0,sum3=0;//临时变量,用于比较
sum1=t[k<<1].lmax;//左儿子
sum2=t[k<<1].sum+t[k<<1|1].lmax;//右儿子
t[k].lmax=max(sum1,sum2);
if(sum1>=sum2)t[k].lright=t[k<<1].lright;//大于等于,满足字典序输出
else t[k].lright=t[k<<1|1].lright;
sum1=t[k<<1|1].sum+t[k<<1].rmax;//左儿子
sum2=t[k<<1|1].rmax;//右儿子
t[k].rmax=max(sum1,sum2);
if(sum1>=sum2)t[k].rleft=t[k<<1].rleft;//大于等于,满足字典序输出
else t[k].rleft=t[k<<1|1].rleft;
sum1=t[k<<1].maxn;//左儿子
sum2=t[k<<1].rmax+t[k<<1|1].lmax;//横跨左右区间
sum3=t[k<<1|1].maxn;//右儿子
int ans=max({sum1,sum2,sum3});//获取最后答案
t[k].maxn=ans;
if(sum1==ans){//获取最后答案所在区间
t[k].mleft=t[k<<1].mleft;
t[k].mright=t[k<<1].mright;
}
else if(sum2==ans){
t[k].mleft=t[k<<1].rleft;
t[k].mright=t[k<<1|1].lright;
}
else{
t[k].mleft=t[k<<1|1].mleft;
t[k].mright=t[k<<1|1].mright;
}
}
Query函数
tree query(int l,int r,int k){//思想与方式与上面基本一致,不再赘述
if(t[k].l>=l&&t[k].r<=r)return t[k];
int mid=(t[k].l+t[k].r)>>1;
if(mid>=r)return query(l,r,k<<1);
else if(l>mid)return query(l,r,k<<1|1);
else{
tree ans1,ans2,ans;
ans1=query(l,mid,k<<1);
ans2=query(mid+1,r,k<<1|1);
ans.l=ans1.l;
ans.r=ans2.r;
ans.sum=ans1.sum+ans2.sum;
int sum1=0,sum2=0,sum3=0;
sum1=ans1.lmax;
sum2=ans1.sum+ans2.lmax;
ans.lmax=max(sum1,sum2);
if(sum1>=sum2)ans.lright=ans1.lright;
else ans.lright=ans2.lright;
sum1=ans2.sum+ans1.rmax;
sum2=ans2.rmax;
ans.rmax=max(sum1,sum2);
if(sum1>=sum2)ans.rleft=ans1.rleft;
else ans.rleft=ans2.rleft;
sum1=ans1.maxn;
sum2=ans2.lmax+ans1.rmax;
sum3=ans2.maxn;
int fmax=max({sum1,sum2,sum3});
ans.maxn=fmax;
if(fmax==sum1){
ans.mleft=ans1.mleft;
ans.mright=ans1.mright;
}
else if(fmax==sum2){
ans.mleft=ans1.rleft;
ans.mright=ans2.lright;
}
else{
ans.mleft=ans2.mleft;
ans.mright=ans2.mright;
}
return ans;
}
}
完整代码
#include<bits/stdc++.h>
using namespace std;
const int N=1000005;
const int inf=0x7fffffff;
struct tree{
int l,r,sum;
int lmax,rleft;
int rmax,lright;
int maxn,mleft,mright;
}t[N<<2];
int a[N],n,m;
int x,y;
void pushup(int k){
t[k].sum=t[k<<1].sum+t[k<<1|1].sum;
int sum1=0,sum2=0,sum3=0;
sum1=t[k<<1].lmax;
sum2=t[k<<1].sum+t[k<<1|1].lmax;
t[k].lmax=max(sum1,sum2);
if(sum1>=sum2)t[k].lright=t[k<<1].lright;
else t[k].lright=t[k<<1|1].lright;
sum1=t[k<<1|1].sum+t[k<<1].rmax;
sum2=t[k<<1|1].rmax;
t[k].rmax=max(sum1,sum2);
if(sum1>=sum2)t[k].rleft=t[k<<1].rleft;
else t[k].rleft=t[k<<1|1].rleft;
sum1=t[k<<1].maxn;
sum2=t[k<<1].rmax+t[k<<1|1].lmax;
sum3=t[k<<1|1].maxn;
int ans=max({sum1,sum2,sum3});
t[k].maxn=ans;
if(sum1==ans){
t[k].mleft=t[k<<1].mleft;
t[k].mright=t[k<<1].mright;
}
else if(sum2==ans){
t[k].mleft=t[k<<1].rleft;
t[k].mright=t[k<<1|1].lright;
}
else{
t[k].mleft=t[k<<1|1].mleft;
t[k].mright=t[k<<1|1].mright;
}
}
void build(int k,int l,int r){
t[k].l=l;
t[k].r=r;
if(l==r){
t[k]={l,r,a[l],a[l],l,a[l],l,a[l],l,l};
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
pushup(k);
}
tree query(int l,int r,int k){
if(t[k].l>=l&&t[k].r<=r)return t[k];
int mid=(t[k].l+t[k].r)>>1;
if(mid>=r)return query(l,r,k<<1);
else if(l>mid)return query(l,r,k<<1|1);
else{
tree ans1,ans2,ans;
ans1=query(l,mid,k<<1);
ans2=query(mid+1,r,k<<1|1);
ans.l=ans1.l;
ans.r=ans2.r;
ans.sum=ans1.sum+ans2.sum;
int sum1=0,sum2=0,sum3=0;
sum1=ans1.lmax;
sum2=ans1.sum+ans2.lmax;
ans.lmax=max(sum1,sum2);
if(sum1>=sum2)ans.lright=ans1.lright;
else ans.lright=ans2.lright;
sum1=ans2.sum+ans1.rmax;
sum2=ans2.rmax;
ans.rmax=max(sum1,sum2);
if(sum1>=sum2)ans.rleft=ans1.rleft;
else ans.rleft=ans2.rleft;
sum1=ans1.maxn;
sum2=ans2.lmax+ans1.rmax;
sum3=ans2.maxn;
int fmax=max({sum1,sum2,sum3});
ans.maxn=fmax;
if(fmax==sum1){
ans.mleft=ans1.mleft;
ans.mright=ans1.mright;
}
else if(fmax==sum2){
ans.mleft=ans1.rleft;
ans.mright=ans2.lright;
}
else{
ans.mleft=ans2.mleft;
ans.mright=ans2.mright;
}
return ans;
}
}
int main(){
cin>>n>>m;
tree ans;
for(int i=1;i<=n;i++){
cin>>a[i];
}
build(1,1,n);
while(m--){
cin>>x>>y;
ans=query(x,y,1);
cout<<ans.mleft<<" "<<ans.mright<<" "<<ans.maxn<<endl;
}
return 0;
}
运行结果:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号