基于朴素贝叶斯的定位算法
http://www.cnblogs.com/LBSer/p/4020370.html
1 定位背景介绍
一说到定位大家都会想到gps,然而gps定位有首次定位缓慢(具体可以参考之前的博文《LBS定位技术》)、室内不能使用、耗电等缺陷,这些缺陷大大限制了gps的使用。在大多数移动互联网应用例如google地图、百度地图等,往往基于wifi、基站来进行定位。
一般APP在请求定位的时候会上报探测到的wifi信号、基站信号。以wifi为例,手机会探测到周围各个wifi(mac地址)对应的信号强度(RSSI),即收集到信号向量(<WF1, RSSI1> <WF2, RSSI2> ... <WFN, RSSIN>)。服务端收到客户端请求后会将信号向量传给定位引擎,定位引擎会结合这些信息返回给服务端定位结果(x, y)、定位精度等信息,服务端再将此结果返回给APP。
定位引擎工作基于两部分:1)大规模的数据收集;2)精细的算法模型。
如图所示,用户在请求app尤其是地图类app的时候,时常会手动开启GPS定位模式,而这时app会将收集到的基站wifi信号以及gps定位到的坐标发送给服务端,服务端将gps定位坐标(x, y)与信号向量(<WF1, RSSI1> <WF2, RSSI2> ... <WFN, RSSIN>)关联起来入库。
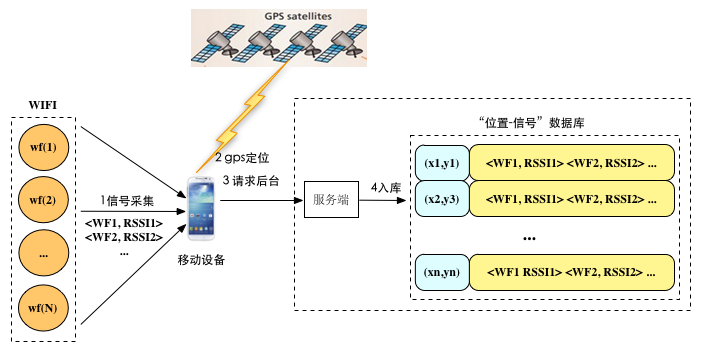
只要用户足够多就能快速积累起大量“位置-信号”数据。如何将这些数据利用起来以实现基于基站wifi的定位将是难题。
通过阅读文献,本文设计了一种基于朴素贝叶斯的定位模型。
2 基于朴素贝叶斯的定位模型
我们从概率的角度看待定位问题。
我们目标是计算在已知信号向量m(<WF1, RSSI1> <WF2, RSSI2> ... <WFN, RSSIN>)的情况下,找到一处位置p使得这种情况的可能性最大,目标公式如下:

直接求解该公式非常困难,但我们可以对该公式进行贝叶斯的转换:
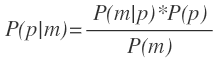
分母P(m)表示信号向量m出现的概率,对于用户这一次请求来说是常量,因此可以忽略,因此目标公式转换为:
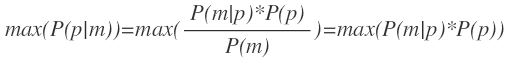
其中P(p)表示位置p出现的概率,P(m|p)表示在位置p出现信号向量m的概率。简化起见我们这里假设位置p出现的概率均等(应该是不均等,比如位置在湖泊中和在市中心大街两者出现的概率显然不一样,以后可以考虑使用此项)。这样目标公式转换为:
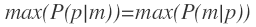
max(P(m|p))指的是在地理空间上找到一个点p,使得信号向量m出现的概率最大。我们可以穷举,计算空间上每一个点出现信号向量m的概率,并找出概率最大的点。由于地理空间是二维平面,存在无穷个点,这种计算不可接受,我们可以通过对地理空间进行网格离散化来简化计算(如下图所示)。我们将地理空间划分为M*N大小的网格(可以通过geohash对网格进行编码,参考之前的博文《geohash》),因此max(P(m|p))就转换为在地理空间找到一个网格,使得信号向量m出现的概率最大。
如何计算某网格p出现信号向量m的概率呢?
通过对“位置-信号”数据库的清洗,可以统计每一个网格出现的信号向量的个数,即得到直方图。

得到了网格p的信号向量直方图后,我们就可以求P(m|p)的概率(p点所在的格子出现信号向量m的概率)。
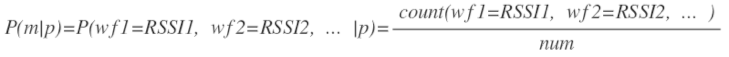
然而实际上,对信号向量进行count几乎不可能,尽管有很多请求百度定位的结果落在网格p内,但这些请求携带的信号向量几乎不一样,想得到有统计意义的直方图几乎不可能。
因此,我们继续对公式进行简化,我们假设各个wifi信号之间相互独立,这个假设也是合理的。于是公式转换为:
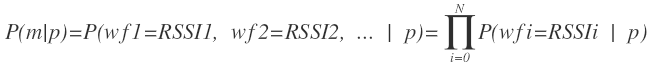
现在问题关键是求解P(wfi=RSSIi | p),即在网格p内,mac地址为wfi且信号强度为RSSIi出现的概率。我们可以事先统计一个网格p内每一个wifi信号的直方图,这样形成统计意义的直方图较容易。
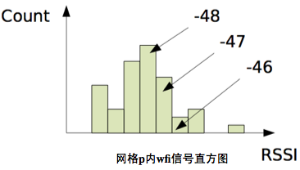
上述模型要求我们对地理空间进行网格化,并预先计算出每个网格内各个wifi对应的信号直方图,并进行存储。然而在实际应用我们网格数目将会非常多,存储直方图的开销较大,因此要尽可能节省网格里携带的信息。因此一种思路是用高斯分布曲线模拟直方图,这样对于一个网格,只需要存储各个wifi对应的高斯分布的几个参数即可。
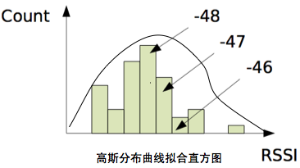
当然,每个网格的直方图曲线并不一定都能用高斯分布曲线来近似,一些文献指出可能存在各种形态的曲线例如双峰曲线等,因此也可以采用核密度估计的方法。
通过上述方法我们可以求出信号向量m出现最大可能性的网格,并取网格的中心点坐标返回即可。当然有些时候很难判别,比如我们求得A和B两个格子的概率几乎相等,这个时候仅仅返回A或者B就不太合适,加权插值是更为合理的选择。一种比较鲁棒的方法是我们找出topk个网格,然后进行插值。

3 问题及解决方法
1)离散网格大小如何确定?
如果网格过小,存储量巨大,并且很多网格没有任何信号直方图;如果过大,精度得不到保证。一种方法网格大小为固定值,根据实验结果来确定网格大小;更好的方法是自适应网格大小,对于信号较密急的地方(市区)网格设小,对于信号稀疏的地方(郊区)网格设大。
2)当用户请求的信号向量里存在一些新的mac地址对应的信号怎么办?
如果直接应用下述公式进行计算,那么得到的概率将会是0,因为我们是概率连乘,只要一项概率为0,整体结果就为0。为了去掉零概率,一个简单的方法是采用加一平滑(add-one smoothing)或称拉普拉斯平滑(Laplace smoothing)。
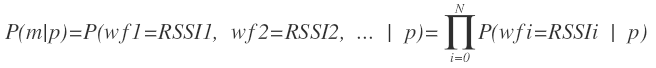
3)如何提高计算效率?
理论上用户来一个请求,我们需要遍历计算数据库每个网格对应的概率,并将最大概率网格对应的中心点返回。假设我们格子是10*10米大小,那么将北京全部网格化就有1.6亿个格子,遍历计算开销十分巨大。
一种提高计算效率的方法是首先根据用户的信号向量求解出大致空间范围,然后计算该空间范围的每一个格子的概率。
4 参考文献
Practical Metropolitan-Scale Positioning for GSM Phones
CellSense: A Probabilistic RSSI-based GSM Positioning System
An Improved Algorithm to Generate a Wi-Fi Fingerprint Database for Indoor Positioning
Topical Issues: Location Fingerprinting
基于区间数聚类的无线传感器网络定位方法
基于一种优化的KNN算法在室内定位中的应用研究


 浙公网安备 33010602011771号
浙公网安备 33010602011771号