快速傅里叶变换FFT修订版
以前我也学习过FFT
但是你也看见了,内容很冗杂,而且当时什么鬼都不懂。
所以写的很马虎
现在我学废了一点点
就回来写了这篇文章。
所以在这片文章里不会有太多的前置知识,需要的知识会使用超链接告诉你。
主要集中在原理方面
最重要一点:
多项式乘法
快速傅里叶变换最简单的用法就是用在多项式乘法
现在给你两个函数\(f,g\)他们的次数分别是\(n_1,n_2\)
那么现在要求\(h=f\cdot g\),他的次数就应该是\(n=n_1+n_2\)(下文的\(n\)就是在这里定义的)
那么我们知道要确定一个\(n\)次的多项式,如果我们把它看作一个函数的话,我们就需要知道在函数图象上的至少\(n\)个点
FFT就是通过构造这\(n\)个点来求出\(h\)的解析式的。
所以就涉及到系数转点值和点值转系数两个关键操作。
系数是什么呢?我们知道我们有一个多项式,用\(f\)举例吧,这是一个\(n_1\)次多项式,所以就可以表示为\(n_1+1\)个单项式相加,他们就是
其中\(a_i\)就被称为\(i\)次项系数我们就可以用\(n_1+1\)个系数来表示一个\(n_1\)次多项式。
同样,我们要知道\(h\)的解析式,我们就需要确定\(n+1\)个系数
然后初中的待定系数法告诉我们,我们有\(n+1\)个未知的系数,我们就需要至少获得\(n+1\)个点
所以我们就取\(n+1\)个互不相同的\(x_i\)代入到\(h(x_i)=f(x_i)\cdot g(x_i)\),就可以求解出\(h\)的解析式。
理论上。
实际实操起来还是比较艰难的。
首先就是怎么选取\(x_i\)
虽然说这个\(x_i\)是随便取的,但是这样我们计算\(n+1\)个点,每个点的时间复杂度都是\(n_1\),这样时间复杂度很不划算,还不如直接\(n_1n_2\)搞暴力。
我们就要取一些\(x_i\)的值,使得这个时间复杂度可以蜜汁迷之降低。
这个我们后面再讨论
快速傅立叶变换
我们先看看我们可以怎么转化掉这个\(f\),把它变成点值。
看好了
这是系数表达方法
然后我们按照次数的奇偶性分类
这样分类之后就出来了两个次数为\(n_1\div 2+1\)的多项式
然后我们是有
是不是很神奇?我也不知道FFT怎么想出来的但是反正成立就行了。
我们就可以抓住这个不放,想一下在这个式子上怎么优化。
我们根据高中时候做偶函数题目的直觉
我们发现后面传进去的都是\(x^2\),唯独前面的系数是一个\(x\)
就是如果没有这个\(x\),我们就会有\(f(x)=f(-x)\)
但是他有
怎么办?
其实也是一样的。你在求\(f(x)\)的时候就要求\(f_0(x^2),f_1(x^2)\)的值,然后在合起来。
那么\(f(x)\)和\(f(-x)\)只是一个系数上的不同,因为这时候你的自变量已经确定了,所以我们可以暂且认为,这两个式子只是在一个系数上不一样。
所以我们在求\(f(x)\)的时候求出来的\(f_0(x^2),f_1(x^2)\)的值在求\(f(-x)\)的时候一样也需要用,这样我们相当于用\(O(1)\)求出了\(f(-x)\)
所以我们只要让我们取的\(x_i\)满足
这样我们就可以把求解的范围缩小一半。
但是这一半貌似不太够。
所以我们观察\(f_0,f_1\)
发现他们也是多项式!
他们转点值也可以这样二分。
前提是满足\(n_1 \div 2 +1\)同样是奇数。
然后他们又二分,又二分。。。
一路二分下去,最后的时间复杂度就降到了\(O(n \log_2n)\)
需要满足的条件就是当前多项式的次数必须是奇数,除非你递归到了边界:0次
所以我们就要求对于所有的次数必须都是偶数,也就是一开始多项式的次数必须是2的整数次幂。
所以前面我们提到的\(n\)(\(\leftarrow\)点一下)最小取值就应该是
然后我们回到\(x_i\)的取值问题。
我们设当前处理的多项式次数为\(m\),很明显这个东西是2的整数次幂。然后\(hf=m\div 2\)
那么我们分出来的两个子函数\(f_0,f_1\)的次数都应该是\(hf\)
然后由\(f_1\)组成\(f\)中次数为奇数的,\(f_0\)组成是偶数的。
那么我们选取这个\(x_i\)就很讲究了,应该要满足
也就是我加上一半的下标之后的数和我是相反数。
那很简单,我们只需要一个数组\(x\),在里面随便构造。
然后你就发现了一个问题。
当你要二分下去的时候,你发现你的子函数。。。他所需要的下标不知道怎么取了吧。。。因为你的子函数除了系数下标奇偶性要考虑之外你还要让他相同的系数代入相同的\(x_i\)
很难取吧。。。
如果你觉得这都有可能的话可以学完单位根的方法之后再把这个方法写出来。
你写的出来,我当场就
把它加入到这个博客里面以表示你的大聪明。
这个时候聪明的不知道谁(FLY?)提出了使用单位根
首先证明充分性,为什么代入单位根可以呢?因为单位根是复数,所以。。。我上面也没说用复数求解不行啊。。。复数求解是可以的,这个理由很充分。
然后我们知道当前处理的多项式的次数\(m\)是2的整数次幂,所以我们的\(m\)一定是偶数,然后我们构造\(m\)次单位根,设他们之中辐角最小的为\(\omega_m\),那么所有的单位根的集合就可以表示为\(\{\omega_m^i|i\in[0,m)\}\)。因为\(\omega_m^0=\omega_m^m=1\)(参考单位根定义)所以这里是左闭右开区间。
就会满足\(hf=m\div 2,\omega_m^i=-\omega_m^{i+hf},i\in[0,hf)\)
所以用单位根也满足了我们的式子\((1)\)(往上翻一翻,在页面右边有标记某个数学公式的编号为\((1)\))
然后证明必要性,我们为什么有使用单位根的必要呢?
这里我们已经通过感性想象知道了使用数组提前搞我是搞不定的。
然后我们看看单位根啊。
按照奇偶性分好子函数之后,他们的次数就是\(hf\)了,他们执行的时候分别构造\(hf\)次单位根,可以保证
我们粗略证明一下,\(hf\)次单位根必定都是\(m\)次单位根。
\((\omega_{hf}^i)^m=(\omega_{hf}^{m=2hf})^i=(\omega_{hf}^{hf})^{2i}=1^{2i}=1\)他的\(m\)次幂为\(1\)他就是\(m\)次单位根。
而且根据一些感性的理解(在单位圆里面隔一个单位根取一个)我们可以得知,这个\(\omega_hf^i\)和子函数获得的系数在原函数里是一一对应的(因为系数也是隔一个取一个才能满足下标的奇偶性相同)
这就完美解决了我们搞不定的问题。
所以我们每次就二分,求解,可以通过\(O(n\log_2n)\)求出\(h\)的点值表达。
快速傅立叶逆变换
上一句话我们说,这个是点值表达。
但是我们需要的是系数表达。
那么我们要给他转换回来。
我们设\(h\)的系数分别是\({a_0,a_1,a_2,\dots,a_{n-1}}\)
然后我们求出来的点值分别是\({y_0,y_1,y_2,\dots,y_{n-1}}\)
那么就应该满足有全称命题\(\displaystyle\forall i\in[0,n),h(\omega_n^i)=y_i\)
把\(h(\omega_n^i)\)暴力拆分一下(貌似这里以前那个还推错了。。。)
看上去还是很难的。
然后我们考虑一下DFT的某些过程
这里是DFT不是FFT
DFT就是离散傅立叶变换,FFT可以认为是求解DFT的一种快速的方法。
求解DFT的正常方法很简单,就是我在开头说的,直接随便取\(n\)个值带入进去完事,不需要什么单位根甚至不需要满足相反数。
这样的做法是很高时间复杂度的。
但是他给我们提供了一个思路
他求点值的方法就是直接暴力。
如果我们代入单位根,但是我们同样暴力。
那么这个过程就变成了一个矩阵乘向量的过程(注意不是矩阵乘法
然后现在倒过来,我知道了等号左边的向量要求右边的向量。
尔曹可知逆元?
算了就是逆矩阵。
我们就有
根据大量的草稿纸和代数运算我们求出中间最大的那个矩阵的逆元
然后我们就发现,我们求\({a_0,a_1,\dots}\)的过程和我们求\({y_0,y_1,\dots}\)的过程是很像的。
只是我们的单位根是倒着取的。这个小小的变动很容易实现,只需要更改一下循环变量的更新就可以了。
然后最后输出的时候不要忘了逆矩阵前面还有一个系数\(\frac1n\)
此处的参考资料:快速傅里叶变换(FFT)——有史以来最巧妙的算法?
Code
#include <cstdio>
#include <cstring>
#include <cmath>
const int N=2097153;
const double Pi=acos(-1.);
struct complex
{
private:
double rl,ige;
public:
inline double real(double a)
{
return rl=a;
}
inline double image(double b)
{
return ige=b;
}
inline double real() const
{
return rl;
}
inline double image() const
{
return ige;
}
complex(double a=0, double b=0)
{
rl=a;
ige=b;
}
inline complex operator+(const complex b)
{
return complex(this->rl+b.rl,this->ige+b.ige);
}
inline complex operator-() const
{
return complex(-rl,-ige);
}
inline complex operator-(const complex b)
{
return *this+(-b);
}
inline complex operator*(const complex b)
{
return complex
(
rl*b.rl-ige*b.ige,
rl*b.ige+ige*b.rl
);
}
};
complex a[N],b[N];
// 注意这里不能用short(我也不知道为什么我卡空间要用short)
long unsigned res[N];
char str[1000001];
unsigned n,m,limit=1;
void FFT(unsigned,complex[],const int=1);
int main()
{
scanf("%s",str);
n=strlen(str);
for(int i=n-1;i>=0;--i) a[i].real(str[n-i-1]-48);
scanf("%s",str);
m=strlen(str);
for(int i=m-1;i>=0;--i) b[i].real(str[m-i-1]-48);
while(limit<(n+m)) limit<<=1;
FFT(limit,a);
FFT(limit,b);
for(int i=0;i<=limit;++i) a[i]=a[i]*b[i];
FFT(limit,a,-1);
for(int i=0;i<=limit;++i) res[i]=(unsigned long)(a[i].real()/limit+.5);
register unsigned bt;
for(bt=0;bt<=limit;++bt)
{
res[bt+1]+=res[bt]/10;
res[bt]%=10;
if(bt==limit&&res[bt+1])++limit;
}
while(bt&&res[--bt]==0);
for(int i=bt;i>=0;--i) printf("%lu",res[i]);
printf("\n");
return 0;
}
void FFT(unsigned limit,complex a[],const int I)
{
if(limit==1) return;
register const unsigned limits=limit>>1;
complex a1[limits+1],a2[limits+1];
for(int i=0;i<=limit;++++i)
{
a1[i>>1]=a[i];
a2[i>>1]=a[i|1];
}
FFT(limits,a1,I); FFT(limits,a2,I);
// 如果是IFFT就是矩阵的逆,单位元逆着取就是了,所以这里的omega作为每次的加量,如果是IFFT需要乘以-1
register const complex omega(cos(2*Pi/limit),I*sin(2*Pi/limit));
register complex root(1);
for(register int i=0;i<limits;++i)
{
a[i]=a1[i]+root*a2[i];
a[i+limits]=a1[i]-root*a2[i];
root=root*omega;
}
}
迭代优化/蝴蝶变换
我们知道,我们上述二分的过程
我们对于每一个子过程都这样执行的话,根据别人的图
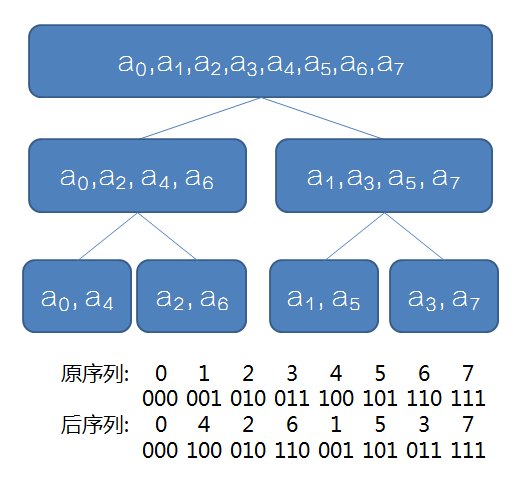
以\(n=2^3\)为例,我们可以发现原序列\(a_1,a_2\dots a_8\),经过二分的“提取”之后,他的序列的下标变了。
不过貌似有一定的规律
我们观察一下这个三位下标,设\(A_i\)表示排在第\(i\)个位置的原序列的下标,\(B_i\)表示后序列下标,那么我们就有
发现了什么规律没有?
通过肉眼观察,我们可以看见,\(B_i\)其实就是\(A_i\)在\(3\)位下的二进制翻转,比如\(A_4=(011)_2\),我们把他从后往前读,就变成了\(B_4=(110)_2\)
那么推广一下,如果当前二项式卷积后的位数是\(n\)位,\(n\)是\(2\)的正整数次幂,那么我们对应的后序列\(B\)就是原序列\(A\)在\(\log_2n\)位下的二进制翻转。
那么我们虽然观察得出了这个规律,但是如果我们
for(int i=0;i<n;++i)
{
b[i]=0;
for(int bit=0;bit<log2(n);++bit)
{
b[i]|= bool(a[i] & (1<<bit)) << (log2(n)-bit); // a[i]=i;
}
}
老是这样检测第\(i\)位,然后用bool转换,然后再位运算,这样的效率未免还是有点低。
我们来观察一下上面的式子,看看有什么规律。
(确实也看不出什么规律)
那么这样呢
\(
B_0=(000)_2,\\
B_1=(100)_2,\quad
B_2=(010)_2,\quad
B_3=(110)_2,\\
B_2=(010)_2,\quad
B_4=(001)_2,\quad
B_5=(101)_2,\\
B_3=(110)_2,\quad
B_6=(011)_2,\quad
B_7=(111)_2\\
\)
如果只看前两列,我们可以看见,第二列就是第一列整体右移一位。
然后再看最后一列:第二列最高位都是\(0\),然后最后一列的最高位就变成了\(1\),剩下的和第二列都是一样的。
然后再来观察一下下标,如果第一列的下标是\(i\),那么这一行第二列和第三列的下标就是\(2i,2i+1\)
那么我们貌似得到了一个结论:随着下标的左移一位,后序列会右移一位;偶数下标加一,后序列最高位会变为1
那么其他情况是不是这样的呢?我们来推广一下
令\(n=2^k,k\in \N^*\)
我们可以知道\(A_i=i\),这是因为原序列。。。就是原下标。
那么一些数的后序列我们就可以得出,就像上面那样。
- 如果原序列我们左移一位,并在最后填0,那么变成后序列,也就是从后往前读,就相当于右移了一位,然后最高位填0。这样我们就可以得到所有的偶数的后序列。
- 如果原序列是偶数,也就是最后一位是0,那么我们加一变成奇数,这个时候最后一位就变成了1,反映在后序列里面就是最高位从0变成了1。这样我们就可以得到所有奇数的后序列
那么我们就可以得出后序列的递推代码了。
B[0]=0;
for(int i=1;i<n;++i)
{
B[i]=
(B[i>>1] >> 1) // 可以通过i/2的后序列得到i的后序列
| // 按位或,用来处理最高位
((i&1) << (k-1)); // 如果是奇数,那么最高位也就是第k位要变成1
}
这样我们就\(O(n)\)搞定了\(O(n\log_2n)\)的二分过程
的一半。
先来总结一下这一半,主要就是在主函数里\(O(n)\)求出后序列,然后再把原序列按照后序列进行下标变换,我们就可以得到以前经过辛苦二分才能得到的序列
这个下标变换,主要就是a[i]=a[b[i]];但是这样会导致一些玄学的覆盖问题,所以我们再观察可以得到,如果\(x\)的后序列是\(x'\),那么\(x'\)的后序列也是\(x\)(翻转两次等于什么都没干),所以我们只需要
if(i<B[i]) swap(a[i],a[B[i]]);
就可以不重不漏实现下标的变换了。
二分是一个分治的过程。我们搞定了前一半:分;现在是时候来走后一半:治。
我们再看回来源于网络的图片

这个治的过程其实我们很熟悉,就是我们在二分的时候调用完子函数再进行的操作。只不过现在我们没有子函数,我们要用一个循环体来搞定子函数做的事。
(这个我熟我就试过广搜求dfs序)
观察,我们这个循环体需要执行\(k\)次,上面那张图少拆了一层,应该拆到最后叶子结点只有一个元素,然后再拼回去。
第\(i\)次需要进行的操作就是将两个长度为\(2^{i-1}\)的区间合并。
这个合并并不是像归并排序那样简单地合并,我们是要根据
来进行合并。具体一点,我们代入的是单位根,所以我们就应该是
这样我们就可以把原来储存着\(f_0,f_1\)的值的\(a\)合并为现在储存\(f\)的值的\(a\)
然后我们用循环体来重复这个合并,就可以做到迭代优化了。
详见代码(卡了常所以有点丑)
#include <cstdio>
#include <iostream>
#include <cmath>
const double PI=acos(-1.);
struct complex
{
double real,image;
inline complex operator +(const complex& n) const
{
return (complex){real+n.real,image+n.image};
}
inline complex operator *(const complex& n) const
{
return (complex){real*n.real-image*n.image,image*n.real+real*n.image};
}
inline complex operator -(const complex& n) const
{
return (complex){real-n.real,image-n.image};
}
}a[2097153],b[2097153];
int n,m,k=0,x,B[2097153];
int limit=1;
inline void FFT(complex[],const int,const int=1);
int main()
{
scanf("%d%d",&n,&m);
for(register int i=0;i<=n;++i)
{
scanf("%d",&x);
a[i].real=x; a[i].image=0;
}
for(register int i=0;i<=m;++i)
{
scanf("%d",&x);
b[i].real=x; b[i].image=0;
}
while(n+m>(1<<++k)); limit=1<<k;
B[0]=0;
for(register int i=1;i<=limit;++i) B[i]=(B[i>>1]>>1)|((i&1)<<(k-1));
FFT(a,limit);
FFT(b,limit);
for(register int i=0;i<=limit;++i) a[i]=a[i]*b[i];
FFT(a,limit,-1);
for(register int i=0;i<=n+m;++i)
{
printf("%d ",int(a[i].real/limit+.5));
}
printf("\n");
return 0;
}
inline void FFT(complex a[],const int limit,const int flag)
{
for(register int i=1;i<limit;++i) // emmm第一个和最后一个怎么换都是自己所以并不需要交换,可以卡常虽然好像没什么用
{
if(i<B[i]) std::swap(a[i],a[B[i]]);
}
for(register int mid=1;mid<limit;mid<<=1)
{
/// 当前处理好多个长度为mid的子区间
// 那么我们就应该取2*mid次单位根,最小单位根的辐角就是(2*PI)/(2*mid)
register const complex omega=(complex){cos(PI/mid),flag*sin(PI/mid)};
for(register int R=mid<<1,j=0;j<limit;j+=R)
{
/// 当前处理一对长度为mid的子区间
// 这对子区间的总长度是R,靠左边的那个子区间的起点是j
register complex root=(complex){1,0};
for(register int opt=0;opt<mid;++opt,root=root*omega)
{
/// 通过第一个区间的第opt位,也就是f_0
/// 和第二个区间的opt位,也就是f_1
/// 通过运算得出合并后应该在这两个位置上的值
register const complex x=a[j+opt], y=root*a[j+opt+mid];
a[j+opt]=x+y; a[j+opt+mid]=x-y;
}
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号