特殊树
首先需要了解树的基础
完全二叉树
首先有一棵满二叉树，给结点顺序编号
然后从大到小把一些结点拿掉，剩下的就是完全二叉树。
（怕你不懂换种方法再说一遍）拿掉的结点满足编号连续，剩下的结点也满足编号连续。
叶子结点只会在最后一层或者倒数第二层。
满二叉树也是一种完全二叉树
一般我们用来写程序的都是完全二叉树，比如说线段树就是在满二叉树上实现的
完全二叉树的数组表示法
。。。这什么大纲我觉得应该是满二叉树的数组表示法。。。
子华神：算啦我哋做人唔好太执着
反正完全二叉树的编号和满二叉树是一样的
根据基础里面，对于每一个结点\(i\)(编号)，它的左右节点（如果有）分别是\(2i,2i+1\)
所以我们就可以用这个性质来表示完全二叉树
首先根节点是1，必须是1。
然后。。。就慢慢推把。。。
定义数组tr[]表示这棵二叉树
我们用堆来讲解这种方法
堆
参考资料
堆是一棵完全二叉树，分为大根堆和小根堆。这里用小根堆讲解
定义数组hp[]表示一个堆
小根堆满足：每一个结点的权值都比它儿子（如果有）的权值小。
对于儿子之间权值的大小没有要求
我们定义\(sze\)表示这个堆的大小（结点数量）
那么堆满足完全二叉树性质，就会有这个大小为\(sze\)的堆结点编号分别为\(1,2,3,\dots,sze\)是连续的
那么插入的时候就是
void insert(int x)
{
/*
向堆中插入一个元素
@param: int x 要插入的元素
@return: void
*/
hp[++sze]=x; // 先把元素扔进去
// 然后调整元素位置使其满足小根堆的性质
int now=sze; // 现在元素x所在的结点编号为now
while(now>1) // 只要还不是根，那么就要判断，如果x比他的父亲小，那么就要让x当父亲，交换他们的值
{
int fa=now>>1;
if(hp[now]>=hp[fa]) return; // 如果当前节点大于等于父节点，那么满足性质，不用改了，直接退出
// 不带等于也可以但是会多执行一次循环，所以为了效率带上等于
swap(hp[now],hp[fa]); // 否则now的值比fa小，不满足堆的性质，那就让now反客为主代替父亲，~~谋权篡位~~
now=fa; // 交换了之后x所在的结点编号为原来的fa,更新
}
}
取出堆首，就直接输出dp[1]
弹出堆首，我们可以考虑直接用堆最后一个元素覆盖堆首，然后sze--，这样就满足完全二叉树编号连续的性质
然后就开始维护堆的性质
void pop()
{
/*
弹出堆首元素
@param: none
@return: void
*/
hp[1]=hp[sze--]; // 直接用堆的最后一个元素覆盖 ，然后维护堆的性质
int now=1;
while(now<<1<=sze) // 有儿子的时候才需要维护它和儿子之间的关系
{
int son=now<<1|
((now<<1|1<=sze)&&(hp[now<<1|1]<hp[now<<1]));
// 使用神奇的位运算装逼
// now<<1|0是左儿子 ,now<<1|1是右儿子
// 右儿子(如果存在)比左儿子小那么就拿右儿子和父亲比较 ，那么就是now<<1|1（后面的表达式的值会是1）
// 否则就拿左儿子和父亲比较，就是now<<1|0（后面的表达式的值会是0）
if(hp[son]>=hp[now]) return; // 如果最小的儿子都比父亲大，那么满足性质，推出
swap(hp[son],hp[now]); // 否则就交换
now=son; // 更新
}
}
完整代码就是
#include <bits/stdc++.h>
using namespace std;
int hp[1000001],sze;
void insert(int x)
{
/*
向堆中插入一个元素
@param: int x 要插入的元素
@return: void
*/
hp[++sze]=x; // 先把元素扔进去
// 然后调整元素位置使其满足小根堆的性质
int now=sze; // 现在元素x所在的结点编号为now
while(now>1) // 只要还不是根，那么就要判断，如果x比他的父亲小，那么就要让x当父亲，交换他们的值
{
int fa=now>>1;
if(hp[now]>=hp[fa]) return; // 如果当前节点大于等于父节点，那么满足性质，不用改了，直接退出
// 不带等于也可以但是会多执行一次循环，所以为了效率带上等于
swap(hp[now],hp[fa]); // 否则now的值比fa小，不满足堆的性质，那就让now反客为主代替父亲，~~谋权篡位~~
now=fa; // 交换了之后x所在的结点编号为原来的fa,更新
}
}
int top()
{
/*
输出堆首元素
@param: none
@return: int 堆首元素的值
*/
return hp[1];
}
void pop()
{
/*
弹出堆首元素
@param: none
@return: void
*/
hp[1]=hp[sze--]; // 直接用堆的最后一个元素覆盖 ，然后维护堆的性质
int now=1;
while(now<<1<=sze) // 有儿子的时候才需要维护它和儿子之间的关系
{
int son=now<<1|
((now<<1|1<=sze)&&(hp[now<<1|1]<hp[now<<1]));
// 使用神奇的位运算装逼
// now<<1|0是左儿子 ,now<<1|1是右儿子
// 右儿子(如果存在)比左儿子小那么就拿右儿子和父亲比较 ，那么就是now<<1|1（后面的表达式的值会是1）
// 否则就拿左儿子和父亲比较，就是now<<1|0（后面的表达式的值会是0）
if(hp[son]>=hp[now]) return; // 如果最小的儿子都比父亲大，那么满足性质，推出
swap(hp[son],hp[now]); // 否则就交换
now=son; // 更新
}
}
int n,opt,x;
int main()
{
cin>>n;
while(n--)
{
cin>>opt;
switch(opt)
{
case 1:
cin>>x;
insert(x);
break;
case 2:
cout<<top()<<endl;
break;
case 3:
pop();
break;
default:
break;
}
}
return 0;
}
哈夫曼树
if(score>=100) prize=0xffff; else
if(score>=80) prize=0xfff; else
if(score>=60) prize=0xff; else
if(score>0) prize=0xf; else
prize=-1;
printf("你总共获得了%d块钱的奖励\n",prize);
这很明显就是学生时代的噩梦产品啦
但是现在告诉你，只有1个人100分，1个人80分，1个人60分，剩下0x7fffffff个人全部都是10分（在(0,60)区间内）
那么我们的代码效率明显就下来了：因为对于剩下的10分的人，我们却每次都要进行4次比较
但是我们调换一下代码顺序
if(score<=0) prize=-1; else
if(score<60) prize=0xf; else
if(score<80) prize=0xff; else
if(score<100) prize=0xfff; else
prize=0xffff;
这样的话我们对于所有的10分的绝大部分人就只需要进行2次比较，大大提升了效率。
但是如果我告诉你0x7fffffff个人都是70分呢？
都是80分？
很难搞了吧
我们想一想在很多人10分的时候为什么第二个的效率比第一个会高
因为少进行了比较，在比较次数较少的情况下就确定了大多数人的情况。
计算机比较是这样的：
- 是情况1吗？是则处理，不是则进入下一步
- 是情况2吗？是则处理，不是则进入下一步
- 是情况3吗？是则处理，不是则进入下一步
...
对于占大多数的10分的人，我只进行了较少（2）次的比较就处理完了。
也就是说我们要搞一个比较顺序，使得数量多的情况先确定下来。比如说我们令情况1为"分数在区间(0,60)内"，那么对于所有10分的人我只需要比较一次，比第二个代码还高效。
那么我们就要来构造这个比较顺序。
首先，我们发现对于每一次判断，只有是/否两个结果，即真/假两个分支。一个合格的比较顺序应该满足所有情况都包含，所以到最后一定会落到一种情况，一定为真。
比如说在第一个代码中
if(score>=100) prize=0xffff; else
if(score>=80) prize=0xfff; else
if(score>=60) prize=0xff; else
if(score>0) prize=0xf; else
prize=-1;
我们会发现这里不外乎五种情况：
score>=100, 80<=score<100, 60<=score<80, 0<score<60, score<=0
我们令score=0,执行一次比较
- score>=100,假，进入情况2
- score>=80,假，进入情况3
- score>=60,假，进入情况4
- score>0,假，进入情况5
- 能进入情况5的score一定都满足小于等于0这个条件，所以一定为真。
这时就发现情况5就是一种一定为真的情况。这种情况下我们可以不需要分支，直接处理。
那么就会变成很多情况：有的情况有两个分支，有的情况没有分支。有分支的情况分支一定指向另一个情况。
那么我们可以用二叉树实现
这就是哈夫曼树，一棵结点的度只为0或2的树。
update 20211029：如果是70分的人最多，那么我们的比较顺序应该这样构造，使得区间\([60,80)\)最先被确定下来
- score>=60吗？是则进入2，否则进入3
- score<80吗？是则进入4，否则进入5
- score>0吗？是则进入6，否则进入7
- 确定下来score的区间为\([60,80)\)，直接处理，是叶子结点
- score<100吗？是则进入8，否则进入9
- 确定下来score的区间为\((0,60)\)，直接处理，是叶子结点
- 进入这种情况一定满足score<=0，直接处理，是叶子结点
- 确定下来score的区间为\([80,100)\)，直接处理，是叶子结点
- 进入这种情况一定满足score>=100，直接处理，是叶子结点
这样构造就满足了区间\([60,80)\)距离根节点最近，距离为2（要比较两次）
这里的根节点表示第一次判断，直到进入4处理\([60,80)\)，总共比较了2次
这里我加粗了叶子结点，发现总共有5个叶子结点，分别对应着五种情况。
哈夫曼树的构造
如果我现在告诉你情况\(i\)出现的次数为\(w_i\),那么我们就此建立哈夫曼树：
- 建立\(n\)个权值分别为\(w_i\)的结点，以他们分别为根建立\(n\)棵树，构成森林\(F\)
根据哈夫曼树的定义，这些情况结点都应该是最终的树的叶子结点，而且\(w_i\)越大的结点应该离根节点越进
那么反过来说，就是\(w_i\)越小的就应该离根节点越远。
我们考虑一下怎么把森林缩成一棵树。
我们可以把一棵树的根删除使其变成一个森林，那么对于森林，我们只需要选随便一个为根，然后剩下的连到这个节点，就很简单构成森林了。
但是由于这里的结点必须都是叶子结点，所以我们就新建一个结点，然后让其他结点连接上来。
但是这里是一棵二叉树，但是叶子肯定不止两个，所以我们要不停新建结点，再把叶子结点连接上来。
所以我们就有了第二步 - 从\(F\)中选择\(i,j\)子树使得\(w_i+w_j\)最小，新建一个结点\(tmp\),使他左儿子为\(i\),右儿子为\(j\),权值\(w_{tmp}=w_i+w_j\)
- 将\(tmp\)加入到\(F\)中，然后从\(F\)中删除\(i,j\)
- 如果\(F\)中只剩下一棵树，那么这棵树就是构造完成的哈夫曼树。
我们看看这样的哈夫曼树有什么性质：
定义结点的路径长度为树根到结点的距离
定义树的路径长度为树上所有结点的结点路径长度之和
定义结点的带权路径长度为结点的路径长度和结点的权值的乘积
定义树的带权路径长度为树上所有结点的带权路径长度之和
那么根据哈夫曼树，权值越大的结点会接近树根，那么路径长度就会小。
在所有叶子结点相同的不同形态的二叉树中，哈夫曼树的带权路径长度最小。
哈夫曼树在编码中的应用
我们知道(char)'A'==(int)65,这是一种编码，ASCII编码是7位2进制编码，至于65是用二进制表示的0b1000001
我们可以理解为我们向别人发送信息"ABCD"的时候是在发送1000001100001010000111000100,这样7位1码叫做等长编码
但是我们发现，如果我们只需要发送大写字母，7位2进制编码可以表示128个字符，然而我们只需要26个字符，这样很浪费。
首先不管字符集中多定义的(128-26)个字符有没有用，我们且说26个字符只需要\(\lfloor log_226\rfloor+1=5\)位二进制表示，然而用ASCII就会用7位，明显浪费。。。
那么我们用5位不就可以了？
可以，但是还不够
我们还可以优化。
我们可以用编码00000表示'A',00001表示'B'......
但是我们知道，字母'E'在英文中出现的次数是最多的，那么我们能不能优化一下，使得'E'的编码最短，这样出来的编码信息就是最短的
比如说我们让'E'的编码为0，那么"EEEEEE"就可以用编码000000来表示，相比之前用5位编码表示一个'E'长度缩短了很多
所以我们可以先定义'E'的编码为0，'A'编码为00，'B'编码为01，然后我们加密"EAB"就会得到编码00001
......
我给你00001，可能的源码就是
"EEEB"
"EAB"
"AEB"
这样不唯一的原因是什么呢？
因为'E'的编码是'A'的编码的前缀，这样就会造成多义性
所以我们在令编码尽量短的前提应该是所有的编码序列\(s\)，满足\(\forall i,j, i\neq j, s_i\mbox{不是}s_j\mbox{的前缀}\)
这个时候哈夫曼树就出来了
我们假设字符\(chr\)在文本中出现了\(w_{chr}\)次，然后用\(w\)构造哈夫曼树，那么在文本中出现次数多的结点就会靠近树根，也就是路径长度短。
我们令结点连向左儿子的边叫0（编号），连向右儿子的边叫1（反过来也可以），那么定义从根节点到叶子结点上的路径的编号连接起来就是这个叶子结点的编码
这样就满足出现次数多的叶子结点离树根近，路径长度短，编码也就短。
而且由于字符\(chr\)一定会出现在叶子结点，而编码是从根节点到叶子结点的路径，不会有一条路径是另一条路径的前缀（参考Trie树,在树上相同的路径就是相同的前缀，只要路径不被完全包含就不是另一个的前缀。然而被完全包含就不会是叶子结点。因此这样出来的编码一定满足两两之间互不为前缀）
这个时候我们看一道题
这是裸的变态哈夫曼树
普通哈夫曼树是二叉的，这道题是\(k\)叉的。但是其实都是一样的，只不过每次从森林中取出的结点的数量是\(k\)个。
所以我们可以编写出来
#include <cstdio> // for scanf,printf
#include <vector> // for std::vector
#include <queue> // for std::priority_queue
struct Node
{
/*
定义树结构体，用指针实现
*/
long long unsigned dat; // 这个结点的权值
Node *sn[10]; // 多叉树，这个结点的儿子们
long long unsigned dep; // 这个结点为根的子树的深度，即这个结点到叶子结点的最长路径长度
Node(long long unsigned d=0) // 初始化
{
dat=d;
sn[0]=sn[1]=sn[2]=sn[3]=sn[4]=sn[5]=sn[6]=sn[7]=sn[8]=sn[9]=NULL;
dep=1;
}
bool operator()(Node *a,Node *b) // 比较函数
{
return a->dat>b->dat; // 要从优先队列中取出最小的元素
}
}*tmp; // 临时变量
int n,k;
std::priority_queue<Node*,std::vector<Node*>,Node> q; // 用优先队列来做森林，每次快速取出森林内最小的结点
void init()
{
/*
初始化
*/
scanf("%d%d",&n,&k);
long long unsigned w;
for(int i=1;i<=n;++i)
{
scanf("%llu",&w);
q.push(new Node(w)); // 先把n个结点放入森林
}
}
Node* merge()
{
/*
构造哈夫曼树
@param: none
@return: Node* 指向哈夫曼树树根的指针
*/
while(!q.empty()) // 循环，应该写死循环但是。。。程序员习惯
{
tmp=new Node; // 新建结点
for(int i=0;i<k&&!q.empty();++i) // 选出最小的结点作为儿子
{
tmp->sn[i]=q.top(); q.pop();
tmp->dep=std::max(tmp->dep,tmp->sn[i]->dep+1); // 更新深度
tmp->dat+=tmp->sn[i]->dat; // 新结点的权值为儿子们的权值的和
}
if(q.empty()) return tmp; // 如果已经取完了，那么tmp就是哈夫曼树的树根指针
q.push(tmp); // 否则就扔到森林中
}
}
long long unsigned query(Node* n,unsigned length=0)
{
/*
统计树的带权路径长度
@param: Node* n 当前结点的指针
unsigned length 当前结点到根节点的距离
@return: 树的带权路径长度
*/
if(n->sn[0]==NULL) return n->dat*length; // 如果没有儿子，那么就是叶子结点，返回
long long unsigned res=0; // 否则就要统计儿子们的带权路径长度
for(int i=0;n->sn[i]&&i<k;++i) res+=query(n->sn[i],length+1); // 带权路径长度之和
return res;
}
int main()
{
init();
Node* ans=merge();
printf("%llu\n%llu\n",query(ans),ans->dep-1);
return 0;
}
然后我们就可以发现第二个样例就错了
按照我们的思路应该：
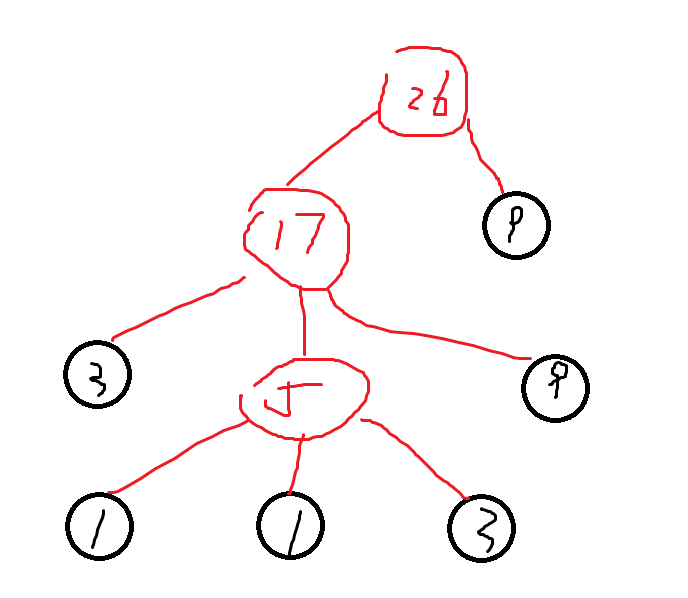
黑结点表示叶子结点，红结点表示新建结点。
然后我们就发现，根节点只有两个儿子，但是根节点明明可以容纳三个儿子。我为什么不把下面的9提上来呢？
这是因为最后我们填充的时候就有0<q.size()<k，那么就填充不满。
所以我们就让它能填充满。
能填充满的话，叶子结点的数量\(n\)和\(k\)之间满足\((k-1)|(n-1)\)
那么我们就向初始的森林中不停填充权值为0的结点使得新的森林中叶子结点数量\(n'\)满足条件
就变成了
void init()
{
scanf("%d%d",&n,&k);
register unsigned muh=(n-1)%(k-1);
if(muh) muh=k-1-muh;
while(muh--) q.push(new Node); // 新建一些权值为0的叶子结点
long long unsigned w;
for(int i=1;i<=n;++i)
{
scanf("%llu",&w);
q.push(new Node(w));
}
}
然后交上去，获得了\(55pts\)的好成绩
为什么呢？
如果两个子树根节点权值都是\(3\),但是一个的深度为\(100\),另一个为\(2\),然后只能选1个的情况下，我肯定选深度为\(2\)的子树才能达到深度最小平衡。
所以我们判断函数就更改一下
bool operator()(Node *a,Node *b)
{
if(a->dat==b->dat) return a->dep>b->dep;
return a->dat>b->dat;
}
总结一下，代码就是
#include <cstdio>
#include <vector>
#include <queue>
struct Node
{
long long unsigned dat;
Node *sn[10];
long long unsigned dep;
Node(long long unsigned d=0)
{
dat=d;
sn[0]=sn[1]=sn[2]=sn[3]=sn[4]=sn[5]=sn[6]=sn[7]=sn[8]=sn[9]=NULL;
dep=1;
}
bool operator()(Node *a,Node *b)
{
if(a->dat==b->dat) return a->dep>b->dep;
return a->dat>b->dat;
}
}*tmp;
int n,k;
std::priority_queue<Node*,std::vector<Node*>,Node> q;
void init()
{
scanf("%d%d",&n,&k);
register unsigned muh=(n-1)%(k-1);
if(muh) muh=k-1-muh;
while(muh--) q.push(new Node);
long long unsigned w;
for(int i=1;i<=n;++i)
{
scanf("%llu",&w);
q.push(new Node(w));
}
}
Node* merge()
{
while(!q.empty())
{
tmp=new Node;
for(int i=0;i<k&&!q.empty();++i)
{
tmp->sn[i]=q.top(); q.pop();
tmp->dep=std::max(tmp->dep,tmp->sn[i]->dep+1);
tmp->dat+=tmp->sn[i]->dat;
}
if(q.empty()) return tmp;
q.push(tmp);
}
}
long long unsigned query(Node* n,unsigned length=0)
{
if(n->sn[0]==NULL) return n->dat*length;
long long unsigned res=0;
for(int i=0;n->sn[i]&&i<k;++i) res+=query(n->sn[i],length+1);
return res;
}
int main()
{
init();
Node* ans=merge();
printf("%llu\n%llu\n",query(ans),ans->dep-1);
return 0;
}
二叉排序树
又称二叉查找树,BST(binary search tree)
平衡树是自平衡的二叉查找树
二叉查找树满足左儿子的权值小于父亲，右儿子的权值大于父亲。
