快速傅里叶变换(FFT)

更好更精简更新的阅读体验（点我）

参考资料：快速傅里叶变换(FFT)详解 - 自为风月马前卒- 博客园

0. 前言

写这篇文章的时候

找不到小学数学笔记本了……

找不到初中数学笔记本了……

找不到高中数学笔记本了……

找不到脑子了……

找不到c++编译环境了……

找不到破解的几何画板了……

找不到Markdown了……

找不到……了

所以推荐在看文章之前推荐把以上东西提前准备好~

本文所有的\(n\)都是\(2\)的整数次幂……

1. 前置知识

我再扔一次目录。觉得自己会的可以跳过……

目录

• 参考资料：快速傅里叶变换(FFT)详解 - 自为风月马前卒- 博客园
  • 0. 前言
  • 1. 前置知识
    • 加法
    • 乘法
    • 乘方
    • 开方
      • 算术平方根
    • 集合
      • 概念
      • 表示
      • 符号们
      • 特性
        • 确定性
        • 互异性
        • 无序性
      • 分类
        • 空集
        • 子集
        • 交集
        • 并集
        • 相对补集
        • 绝对补集
        • 幂集(好像不要求掌握)
        • 区间
        • 相等集合
      • 表示方法
        • 列举法
        • 描述法
        • 图像法
        • 符号法
    • 多项式
      • 系数表示法
      • 点值表示法
      • 简单介绍一下DFT和IDFT
    • 三角函数
      • 角
      • 象限角
      • 圆
        • 圆周角与圆心角
        • 角度的弧度制
      • 函数
        • 定义域
        • 值域
        • 对应法则
      • 反函数
      • 初中的三角函数
      • 任意角的三角函数
      • 诱导公式
      • 三角函数的反函数
      • 补：三角形的面积公式
      • 三角函数的和角公式
        • 正弦
        • 余弦
    • 复数
      • 向量
      • 向量的模
      • 向量加法
        • 三角形法则
        • 平行四边形法则
      • 矢量乘法
        • 数乘
        • 数量积
        • 向量积
      • 复数
        • 虚数
        • 复数
        • 共轭复数
      • 复平面
      • 模长
      • 辐角
      • 复数乘法

    • 单位根

      • 性质
  • 2. 快速傅里叶变换(FFT)
  • 3. 快速傅里叶逆变换(IFFT)
• 总结一下
• 代码实现
  • 递归实现
  • 迭代优化
• 补充：符号们
• 补充：快读快写

开始进入正题……

加法

不想讲……

乘法

乘法运算的结果叫做积

很多情况下，\(a \times b = a \cdot b = ab\)

$a \times b = \underbrace{a + \dots + a}\limits_{b个a} $

同时在乘法这里讲一下累加

\(\sum_{i = l}^{r} a_i = \displaystyle \sum_{i=l}^{r} a_i = a_l + a_{l + 1} + \dots + a_{r - 1} + a_r\)

也可以讲一下累乘

\(\prod_{i = l}^{r} a_i = \displaystyle \prod_{i = l}^{r} a_i = a_l \times a_{l + 1} \times \dots \times a_{r - 1} \times a_r\)

乘方

乘方的结果叫做幂(power)，

\(a^b = \underbrace{a \times \dots \times a} \limits_{b个a}\)

这里\(a\)叫做底数，\(b\)叫做指数。

根据上面的式子，可以推出

\[a^b \times a^c = \underbrace{a \times \dots \times a}\limits_{b个a} \times \underbrace{a \times \dots \times a} \limits_{c个a} = \underbrace{a \times \dots \times a} \limits_{(b+c)个a} = a^{b+c} \]

以及同理可得\(a^b \div a^c = a^{b-c}\)

所以我们也可以知道\(a^0 = 1 | a \in \R \cup \C, a \neq 0\)

至于集合什么的……我们留到后面吹

为什么要强调\(a \neq 0\)？

因为\(0^0\)没有意义

我们可以知道一个\(0\)相乘是\(0\)， 就是\(0^1 = 0\)，然后\(0^0=0^1\div0^1=0\div0\)

小学老师告诉过我们，\(0\)除以任何非零数都是\(0\)，\(0\)不能作除数，\(0\div0\)没有意义

我们来设一下\(a\div b =c\)，即\(a = b\times c\)

如果\(b = 0, a \neq 0\)，解关于\(c\)方程告诉我们无解……

如果\(a = 0, b = 0\)，解关于\(c\)的方程告诉我们有无数个解……

所以没有意义。

所以整篇文章我们都默认底数不为\(0\)

开方

开方是乘方的逆运算。

数\(a\)的\(n\)（\(n\)为自然数）次方根指的是n方幂等于a的数，也就是\(b|b^n = a, n \in \N\)。(转自百度百科)

当\(n=2\)时称\(b\)为\(a\)的平方根，\(n=3\)时成为立方根。所有的次方根统称方根

算术平方根

\(a\)的算术平方根是平方为\(a\)的非负数，即\(b|b^2=a,b\geq 0\),也可以写成\(b=\sqrt[2]{a}=\sqrt{a}\)

知道这个之后我们就可以发现

\[a^b \times a^b = a^{b + b} = a^{2b}\\ \therefore \sqrt{a^{2b}} = a^b \]

所以我们也可以推出\(\sqrt[m]{a^b} = a^{\frac{b}{m}}\)

但是当\(b\)不能整除\(m\)的时候……

其实也是可以计算的

举个栗子

\[4^{1.5} = 4^{\frac{3}{2}} = \sqrt[2]{4^3} = \sqrt[2]{64} = 8 \]

栗子吃完了，你也该懂了……

现在来说说负数次幂

其实很简单啦……

设\(b-c=m\)，则有\(a^b \div a^c = a^m\)

当\(m<0\),即\(b<c\),

\[a^m=a^b \div a^c = (\underbrace{a \times \dots \times a} \limits_{b个a}) \div (\underbrace{a \times \dots \times a} \limits_{c个a}) = 1 \div(\underbrace{a \times \dots \times a} \limits_{c-b个a}) = \frac{1}{a^{c-b}} \]

所以知道了吧，\(a^b = \frac{1}{a^{-b}}\)，这样转换过来就可以计算出负次数幂。

集合

我感觉我在讲数学……

转自百度百科：

概念

集合是指具有某种特定性质的具体的或抽象的对象汇总而成的集体。其中，构成集合的这些对象则称为该集合的元素

表示

假设有实数\(x < y\)：

1. \([x，y]\) ：方括号表示包括边界，即表示大于等于\(x\)、小于等于\(y\)的数。

2. \((x，y)\)：小括号是不包括边界，即表示大于\(x\)、小于\(y\)的数。

符号们

写在后面了……（因为太长了）给你们一个目录超链接去看吧……

特性

确定性

给定一个集合，任给一个元素，该元素或者属于或者不属于该集合，二者必居其一，不允许有模棱两可的情况出现。

互异性

一个集合中，任何两个元素都认为是不相同的，即每个元素只能出现一次。有时需要对同一元素出现多次的情形进行刻画，可以使用多重集，其中的元素允许出现多次。

无序性

一个集合中，每个元素的地位都是相同的，元素之间是无序的。集合上可以定义序关系，定义了序关系后，元素之间就可以按照序关系排序。但就集合本身的特性而言，元素之间没有必然的序。

分类

空集

不包含任何元素，如\(\left \{x|x \in \R, x^2+1 = 0\right \}\)，在实数范围内方程无解，所以该集合是空集,用\(\emptyset\)表示。他有两个特点

1. 空集\(\emptyset\)是任意一个非空集合的真子集。
2. 空集\(\emptyset\)是任意一个集合的子集

子集

设\(S, T\)是两个集合，如果\(S\)的所有元素都属于\(T\), 即\(x \in S \Rightarrow x \in T\), 则称\(S\)为\(T\)的子集,记为\(S \subseteq T\)

显然，对于任何集合\(S\)，都有\(S \subseteq S\), \(\emptyset \subseteq S\),其中，符号\(\subseteq\)读作包含于，表示该符号左边的集合中的元素全部是该符号右边集合的元素。

如果\(S \subseteq T\), 但\(T\)中存在一个元素\(x\), \(x \in T, x \notin S\), 即\(S \neq T\), 则称\(S\)为\(T\)的一个真子集,即 \(S \subsetneq T\)或者\(S \subset T\)

交集

由属于A且属于B的相同元素组成的集合，记作\(A \cap B\) 或\(B \cap A\)，读作“A交B”（或“B交A”），即\(A \cap B = \left\{x|x \in A, x\in B \right\}\).注意交集越交越少。若A包含B，则\(A\cap B=B，A\cup B=A\)

并集

由所有属于集合A或属于集合B的元素所组成的集合，记作\(A\cup B\)（或\(B\cup A\)），读作“A并B”（或“B并A”），即\(A\cup B=\left \{x|x\in A,x\in B\right \}\).注意并集越并越多，这与交集的情况正相反

相对补集

由属于A而不属于B的元素组成的集合，称为B关于A的相对补集，记作\(A-B\)或\(A \mbox{\\} B\)，即\(A-B=\left \{x|x\in A，x\notin B\right \}\)

绝对补集

\(A\)关于全集合\(U\)的相对补集叫做\(A\)的绝对补集，记作\(A'\)或\(\mbox{~}A\)

幂集(好像不要求掌握)

设有集合A，由集合\(A\)所有子集组成的集合，称为集合\(A\)的幂集。对于幂集有定理如下：有限集\(A\)的幂集的基数等于\(2\)的有限集\(A\)的基数次幂

区间

设\(a, b\quad(a < b)\)是两个相异的实数，则满足不等式\(a < x < b\)的所有实数\(x\)的集合称为以\(a, b\)为端点的开区间，记为\((a, b)=\left \{x : a < x < b\right \}\)

满足不等式\(a \leq x \leq b\)的所有实数\(x\)的集合成为以\(a, b\)为端点的闭区间，记为\([a, b] = \left \{x: a \leq x \leq b \right \}\)

满足不等式\(a < x \leq b\)或不等式\(a \leq x < b\)的所有实数\(x\)的集合称为以\(a, b\)为断电的半开半闭区间，分别记为\((a, b] = \left \{x: a < x \leq b \right \}\) 和 \([a, b) = \left \{x: a \leq x < b \right \}\)

除此之外，还有下述几类无限区间：(因为无限取不到，所以无限那半边肯定是开区间)

\[(a, +\infty) = \left \{x : x > a \right \}\\ (-\infty, b) = \left \{x : x < b \right \}\\ [a, +\infty) = \left \{x : x \geq a \right \}\\ (-\infty, b] = \left \{x : x \leq b \right \}\\ (-\infty, +\infty) = \R \]

相等集合

如果两个集合\(S\) 和 \(T\)的元素完全相同，则称\(S\)与\(T\)两个集合相等，记为\(S=T\) 。显然有如下关系：

\[S=T \Leftrightarrow S\subseteq T \wedge T \subseteq S \]

表示方法

列举法

举法就是将集合的元素逐一列举出来的方式。例如，光学中的三原色可以用集合{红，绿，蓝}表示；由四个字母\(a,b,c,d\)组成的集合\(A\)可用\(A={a,b,c,d}\)表示，如此等等。

列举法还包括尽管集合的元素无法一一列举，但可以将它们的变化规律表示出来的情况。如正整数集\(\N_+\)和整数集\(\Z\) 分别可以表示为\(\N_+ = \left \{1, 2, 3 \cdots, n, \cdots \right \}\) 和\(\Z = \left \{0, \pm1, \pm 2, \cdots, \pm n, \cdots \right \}\)

描述法

描述法的形式为{代表元素|满足的性质}。

设集合\(S\)是由具有某种性质\(P\)的元素全体所构成的，则可以采用描述集合中元素公共属性的方法来表示集合：\(S={x|P(x)}\)。例如，由2的平方根组成的集合B可表示为\(B={x|x^2=2}\)。

而有理数集\(\Q\)和正实数集\(\R^+\)可以表示为\(\Q = \left \{x|x=\frac{q}{p}, p \in \N^+ , q \in \Z \right \}\) 和 \(\R^+ = \left \{x: x \in \R \wedge x > 0 \right \}\)

图像法

略……

符号法

有些集合可以用特殊符号表示，例如：

\(N\)：非负整数集合或自然数集合\({0,1,2,3,…}\)

\(N^*\)或\(N^+\)：正整数集合\({1,2,3,…}\)

\(Z\)：整数集合\({…,-1,0,1,…}\)

\(Q\)：有理数集合

\(Q^+\)：正有理数集合

\(Q^-\)：负有理数集合

\(R\)：实数集合(包括有理数和无理数）

\(R^+\)：正实数集合

\(R^-\)：负实数集合

\(I\)：虚数集合

\(C\)：复数集合

\(\emptyset\) ：空集（不含有任何元素的集合）

(我集合好像没有讲很久吧……)

多项式

系数表示法

就是……关于\(x\)的一个多次的式子加起来。

若\(f(x)\)表示一个关于\(x\)的\(n - 1\)次多项式，那么就会有

\(f(x) = \displaystyle \sum _ {i = 0} ^ {n - 1} a_i \times x^i\)

我们可以发现对于固定的\(x\), \(x^0, x^1, \cdots , x^n\)都是固定的

所以表示一个多项式我们也可以去掉\(x\)，直接表示成\(f(x) = a_0, a_1, a_2 \cdots a_{n - 1}\),这就是我们平时见到的多项式（？）

点值表示法

不知道什么时候我们看了一眼函数

比如说二次函数\(y=ax^2+bx^1+cx^0\),对比一下\(x\)的二次多项式\(f(x)=a_2x^2+a_1x^1+a_0x^0\)

是不是很像？

如果对于每一个\(f(x)\)我们都把\(a_0, a_1, \cdots , a_{n-1}\)都看做常数的话，我们再在平面直角坐标系上画出\(y=f(x)\)，可以发现这就是关于\(x\)的多次函数

只要我们确定了\(a_i (0\leq i\leq n - 1)\)这\(n\)个点，我们就确定了一个关于\(x\)的\(n-1\)次函数

简单介绍一下DFT和IDFT

顺便说一下一些容易混淆的概念：

DFT：离散傅里叶变换，\(O(n^2)\)计算多项式乘法

FFT：快速傅里叶变换，\(O(nlog_2 n)\)计算多项式乘法

FNTT/NTT：快速傅里叶变换的优化版，优化常数及误差

FWT：快速沃尔什变换，利用类似FFT的东西解决一类卷积问题

MTT：毛爷爷的FFT，非常nb，任意模数

FMT：快速莫比乌斯变化，干嘛的原文没写……

究竟DFT和FFT是干嘛的呢

我们通过一道裸题了解一下

题目描述

给定一个n次多项式F(x)，和一个m次多项式G(x)。
请求出F(x)和G(x)的卷积。

输入

第一行2个正整数n,m。
接下来一行n+1个数字，从低到高表示F(x)的系数。
接下来一行m+1个数字，从低到高表示G(x)的系数。

输出
一行n+m+1个数字，从低到高表示F(x)∗G(x)的系数。对998244353取模。

样例输入
1 2
1 2
1 2 1
样例输出
1 4 5 2

一道很裸的模拟高精度乘法（？）（反正思路差不多，都要一个个乘）

那么时间复杂度是多少呢？

保守估计\(O(n^2)\)左右……

好了我没把提示放出来给你们看……

提示
样例解释：(2x+1)*(x^2+2x+1)=2x^3+5x^2+4x+1
故输出 1 4 5 2

两组数据，n,m<=1000000，0<=系数<=9
本题可能需要一定程度上的卡常

你还敢使用那个平方级别算法吗？

再告诉你一句话，这是个模板题

这个时候就需要我们学习一个令人窒息的操作：FFT

不过我们还是要先介绍一下傅里叶变换

前面已经说过，如果确定了\(a_i (0\leq i \leq n - 1)\),那么我们就可以确定\(n-1\)次函数.

所以对于两个关于\(x\)的\(n\)次多项式，我们可以整俩\(n\)次函数。

先把系数转为点值，然后把两个乘起来。

最后转回去。

这样每次乘法就是\(O(1)\),总共就可以\(O(n)\)暴虐多项式乘法。

是不是很棒？

算了吧……

正常的系数转点值叫做DFT(傅里叶变换)

正常的点值转系数叫做IDFT（离散傅里叶变换）

这两个东西都是\(O(n^2)\)级别的

所以使用傅里叶变换，你就把\(O(n^2)\)的东西变成了\(O(n^2+n)\)

那我要你有何用

那咋整。

总不能说了这么多东西白说吧……

我们可以问一下傅里叶

我们可以用不正常的转换方法

诶别用删除线。

就是用不正常的转换方法

我们知道根据点值，我们每次会有点\((x, y)\)，只靠实数是无法优化的了。

但是我们还有虚数

还有复数。

随便用。

但在此之前还是要把我们的前置知识铺垫好。

三角函数

在讲三角函数值钱我们应该先讲一下角……

角

初中老师告诉过我们：

具有公共端点的两条射线组成的图形叫做角。这个公共端点叫做角的顶点，这两条射线叫做角的两条边。（静态定义）

但是初中老师好像不会教你傅里叶变换

所以我们翻到高中的定义：

一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形叫做角。所旋转射线的端点叫做角的顶点，开始位置的射线叫做角的始边，终止位置的射线叫做角的终边。（动态定义）

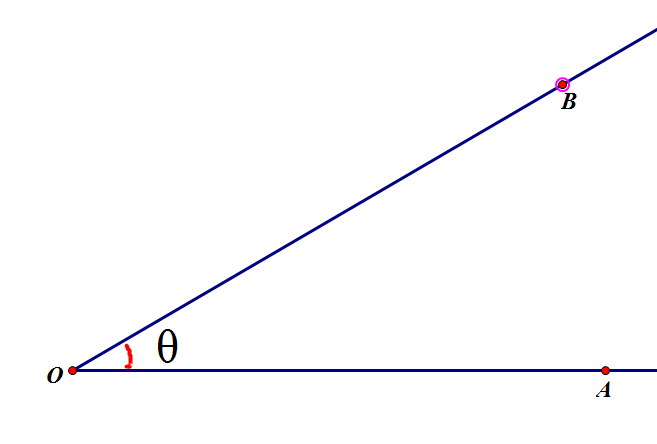
这里射线\(OA\)绕点\(O\)旋转至射线\(OB\)

当然初中老师也不会跟你讲负角，不会跟你讲大于180°的角

现在我来告诉你

如果旋转方向是逆时针，那么这个角叫做正角，大小为\(\Theta\),符号为\(+\),合起来就是\(\angle AOB = +\Theta\)

（一般正号省略）

如果旋转方向是顺时针，那么这个角叫做负角，大小为\(\Theta\),符号为\(-\),合起来就是\(\angle AOB = -\Theta\)

注意：这里的符号仅表示方向，不表示大小

如果比较大小的话，\(-20° > 5 °\)

舒服不？

还有一种角叫做零角，就是不旋转。

象限角

有平面直角坐标轴和一个角，角的始边与坐标轴\(x\)的非负半轴重合，顶点和原点重合，终边在哪个象限这个角就是什么象限角。

特别地，当终边在坐标轴上时，这个角不属于任何一个象限。

圆

别问我为什么讲角要讲圆

根据定义，圆就是在一个平面内，一个动点以一个定点为中心，以一定长度为距离旋转一周形成的封闭图形。

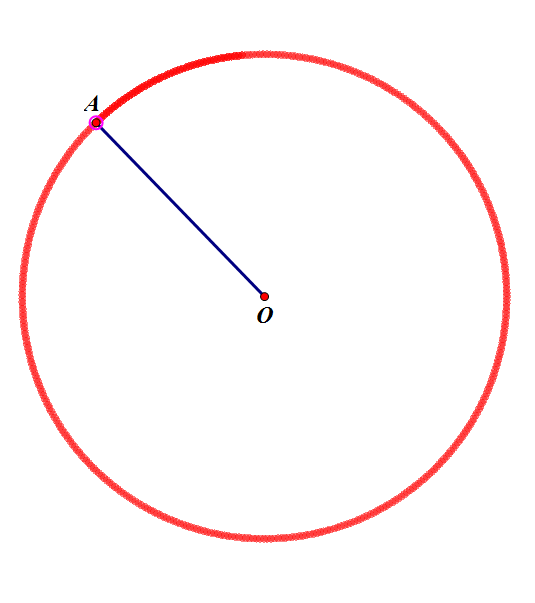
别问我圆怎么追踪出来的

\(O\)为定点，\(OA\)为定长，\(A\)的运动轨迹形成的封闭图形就是\(\circ O\)

圆周角与圆心角

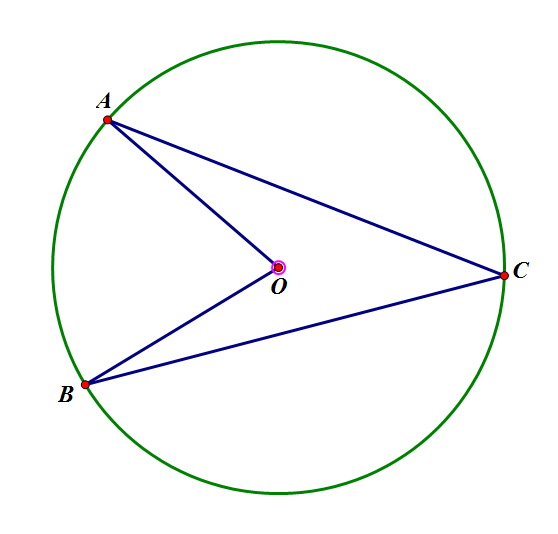
这圆绝对不是追踪出来的

圆心角是指在中心为O的圆中，过弧\(\mathop{AB}\limits^{\frown}\)两端的半径构成的\(\angle AOB\)， 称为弧\(\mathop{AB}\limits^{\frown}\)所对的圆心角。

顶点在圆上，并且两边都和圆相交的角叫做圆周角，这一定义实质上反映的是圆周角所具备的两个特征：

1. 顶点在圆上。
2. 两边都和圆相交。这两个条件缺一不可。

同样也有一个简单的性质，同弧或等弧所对的圆心角相等，圆心角等于同一弧所对的圆周角的两倍。百度上有非常简明易懂的证明……这里篇幅估计已经超了……

角度的弧度制

有没有在一些书上听说过\(\pi\)不是圆周率的？

这个时候就是弧度制的问题了

首先弧度制，我们就要把角放在一个圆里面。

让这个角的定点和圆心重合，对，就是让他变成圆心角。

弧度制是用弧长和半径之比来度量对应的圆心角角度的方式。用符号\(rad\)表示，读作弧度，一般忽略。

所以以后看见\(\angle A =1\)不是一度的意思，是一弧度的意思。因为它没带单位

那么一弧度是多少度呢？

都说了是用弧长和半径的比来度量了……

那么当弧长等于半径的时候，这个弧所对的圆心角就是1弧度

百度是这样说的：

等于半径长的圆弧所对的圆心角叫做1弧度的角。

由于圆弧长短与圆半径之比，不因为圆的大小而改变，所以弧度数也是一个与圆的半径无关的量。角度以弧度给出时，通常不写弧度单位。

然后我们再推算一下

设在\(\circ O\)中，\(\angle AOB = 1rad = x °\),半径为\(r\),根据弧长等于半径可以得到\(\mathop{AB} \limits^{\frown} = r = 2\pi r \times \frac{x}{360}\),可以得到等式\(r = \frac{\pi r x}{180}\)

化简之后得到\(x = \frac{180}{\pi}\)

也及时\(1 (rad) = \frac{180°}{\pi}\)

那么\(180° = \pi (rad)\)就是移个项的事而已……

为什么我们要用弧度制呢？

为了方便计算。

弧度制下的角的大小，是一个实数，可以和其他数字比较大小。而角度制下只是一个角度。

还有一个很重要的原因：作为程序猿，我相信你不知道（我才知道）（看好了）：

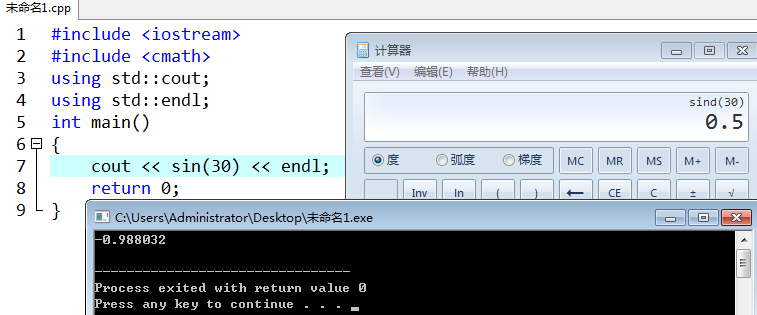
当然，这里计算器没有错，C++也没有错

只是他们的单位不一样而已

计算器计算的是\(\sin 30°\)，C++ 计算的是\(\sin 30 (rad)\)

如果我们修改一下，在C++里面输入\(\sin(3.1415926)\),或者更精准一点，输入\(\sin(\pi)\)

这里拓展一个小知识，acos()是cos()的反函数，即\(acos(\cos(x)) = x\)

后面我们会告诉你\(\cos(\pi(rad)) = -1\),这里你只需要知道$acos(-1) = \pi $就可以了

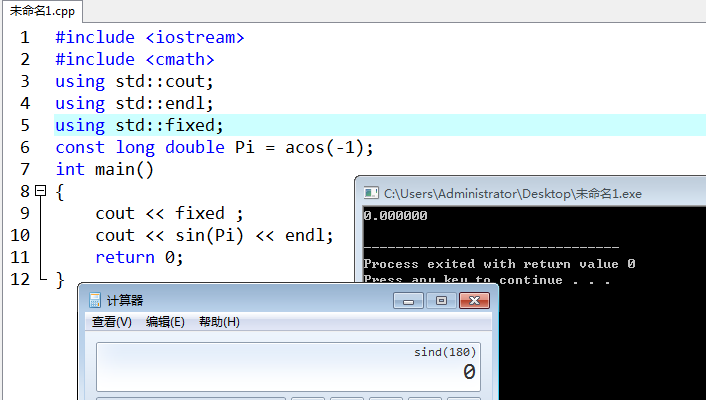
舒服了吗？

C++里面是弧度制计算的。

所以我们要学习弧度制。

函数

普通的函数概念就不在这里讲了……

我们只来补充一下函数三要素：定义域，值域和对应法则

看一下对于函数\(y=f(x)\)

定义域

指的就是自变量\(x\)的取值范围

如果\(f(x) = \sqrt[2]{x}\),在实数范围内，这个函数的定义域（\(x\)的取值范围）就是区间\([0, +\infty)\)

如果\(f(x) = x\),在实数范围内，这个函数的定义域就是区间\((-\infty, +\infty)\)

值域

在函数经典定义中，随自变量改变的因变量改变的取值范围叫做这个函数的值域，在函数现代定义中是指定义域中所有元素在某个对应法则下对应的所有的象所组成的集合。如：f(x)=x，那么f(x)的取值范围就是函数f(x)的值域。

百度百科的解释是不是太长了？

没关系我们来举个栗子。

如果\(f(x) = x ^2\)，很明显这个函数的定义域是所有实数，那么根据平方非负，我们可以知道这个函数的值域就是区间\([0, +\infty)\)

如果\(f(x) = x\)，这个函数的定义域是\((-\infty, +\infty)\),值域是\((-\infty, +\infty)\)

对应法则

对于函数\(y = f(x)\)来说，\(f\)指的就是一个对应法则。

若函数的定义域为\(A\),值域为\(B\),

则\(y = f(x)\)表明，$\forall _{x \in A}, \exist! _{y \in B} \quad \text{使得}y = f(x) $

即对于定义域中所有\(x\)的值，在对应法则\(f\)的作用下，可以得到值域中唯一的\(y\)的值

反函数

设有函数\(y=f(x)\),定义域是\(D\), 值域是\(f(D)\)

如果有一个对应法则\(g\),使得\(\forall _{y \in f(D)}, \exist! _{x \in D} \quad \text{使得} x = g(y)\)

那么按照法则\(g\)得到了一个定义域是\(f(D)\)，值域是\(D\)的函数，我们把\(g\)成为\(f\)的反函数

记为\(g = f^{-1}\), \(x = f^{-1}(y), y \in f(D)\)

由此易得，\(g\)的反函数是\(f\),也就是\(f\) 和 \(f^{-1}\)互为反函数。

同样我们也很容易得到\(f(g(x)) = x\)

而且\(y=f(x)\)与\(y=f^{-1}(x)\)关于直线\(y=x\)对称

证明：设点\((a, b)\)是\(y=f(x)\)上的一点，则\(b = f(a)\)

然后我们用反函数代进去，\(y=f^{-1}(x)\), \(f^{-1}(b) = a\),所以点\((b, a)\)在函数\(y = f^{-1}(x)\)上

易得（感性理解一下就好）\((a, b)\) 和 \((b, a)\)关于直线\(y = x\)对称

由\(a, b\)的任意性可知，\(y=f(x)\) 和 \(y = f^{-1}(x)\)关于直线\(y=x\)对称

---

初中的三角函数

在讲三角函数之前，我应该先贴一幅图

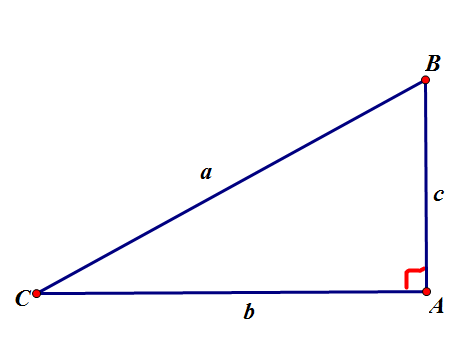
初中学的三角函数应该仅限于锐角三角形

设三角形\(\triangle ABC\)中\(\angle A ,\angle B, \angle C\)所对的边分别是\(a, b, c\)，那么\(\sin C = \frac{c}{a}, \cos C = \frac{b}{a}, \tan C = \frac{\sin C}{\cos C} = \frac{c}{b}\)

除了商数关系\(\tan C = \frac{\sin C}{\cos C}\)之外，还有平方关系\(\sin^2 C + \cos^2 C = 1\)

特别的，\(\angle A = \frac{\pi (rad)}{2}\)时，\(\sin A = \frac{a}{a} = 1\),虽然根据常规的方法我们不知道哪条是\(\angle A\)的邻边，但是根据平方关系我们可以解得\(\cos^2 A = 0\), 即\(\cos A = 0\),这个时候根据商数关系就没有$\tan A $了

然后我们开始讲任意角的三角函数

任意角的三角函数

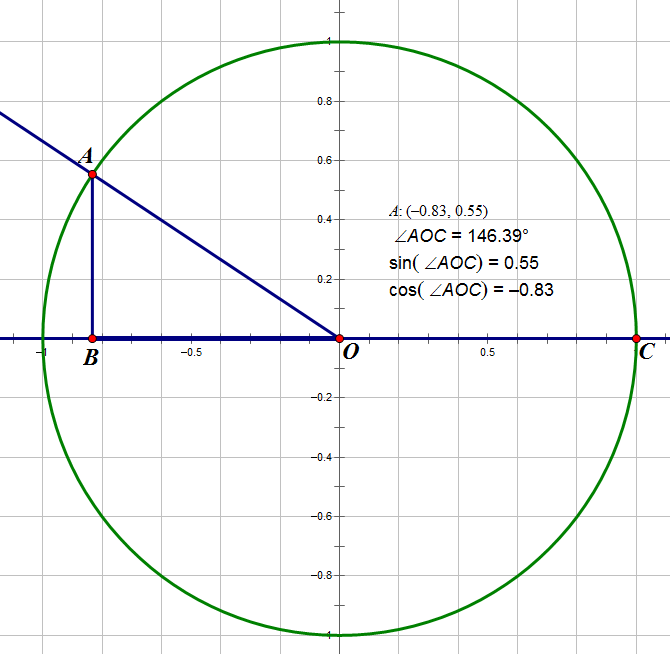
在平面直角坐标系中作单位圆（就是半径为1的圆啦），\(\angle AOC\)的始边\(OC\) 和 \(x\)轴非负半轴重合，顶点\(O\)与直面直角坐标系顶点\(O\)重合，终边\(OA\)交单位圆于点\(A\)

易得\(OA\) = 1

我们可以脑补一下当$\angle AOC $ 为锐角的时候，这个时候\(\sin \angle AOC = \frac{AB}{AO} = \frac{AB}{1} = AB = y_A\), 同理可得\(\cos \angle AOC = x_a\)

其实你已经得出了任意角三角函数的一个巧妙的计算式了。

对于任意角\(\angle AOC\), 令\(OA\)交单位圆于点\(A\),都有\(\sin \angle AOC = y_A, \cos \angle AOC = x_A\)

可以求得\(\tan \angle AOC = \frac{y_A}{x_A}, \angle AOC \neq \frac{\pi}{2}, \cot \angle AOC = \frac{x_A}{y_A}, \angle AOC \neq \pi\)

诱导公式

这里直接给出公式，推理方面嘛……自己画个单位圆，再画两个角，用终边和单位圆的交点的坐标推理一下就知道了

角度	\(\alpha\)	\(\alpha+2k\pi(k\in \Z)\)	\(-\alpha\)	\(\pi + \alpha\)	\(\pi - \alpha\)	\(2\pi - \alpha\)	\(\frac{\pi}{2} \pm \alpha\)
\(\sin\)	\(\sin \alpha\)	\(\sin \alpha\)	\(-\sin \alpha\)	\(-\sin \alpha\)	\(\sin \alpha\)	\(-\sin \alpha\)	\(\cos \alpha\)
\(\cos\)	\(\cos \alpha\)	\(\cos \alpha\)	\(\cos \alpha\)	\(-\cos \alpha\)	\(-\cos \alpha\)	\(\cos \alpha\)	\(\mp \sin \alpha\)
\(\tan\)	\(\tan \alpha\)	\(\tan \alpha\)	\(-\tan \alpha\)	\(\tan \alpha\)	$-\tan \alpha $	\(-\tan \alpha\)	\(\mp \cot \alpha\)
\(\cot\)	\(\cot \alpha\)	\(\cot \alpha\)	\(-\cot \alpha\)	\(\cot \alpha\)	\(-\cot \alpha\)	\(-\cot \alpha\)	\(\mp \tan \alpha\)

三角函数的反函数

\(\sin ^ {-1} = asin\), \(\cos ^ {-1} = acos\)

知道这两个应该够了……

补：三角形的面积公式

小学老师是不是告诉过你们

\(S_{\triangle ABC} = AB \times CD \div 2\)

相信不用我说你也知道作\(CD \bot AB\)于\(D\)

但是老师们基本不会告诉你们\(S_{\triangle ABC} = AB \times AC \times \sin \angle BAC \div 2\)

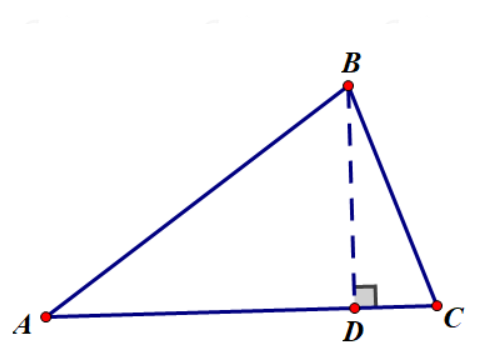
我们可以知道\(S_{\triangle ABC} = \frac{AC \times BD}{2}\)

而且我们也知道\(BD = \sin A \times AB\),

代回去：\(S_{\triangle ABC} = \frac{AC \times \sin A \times AB}{2} = \frac{\sin A \times AB \times AC}{2}\)

所以三角形面积也可以等于任意两条边的乘积再乘上夹角的正弦的一半

三角函数的和角公式

正弦

当然\(\sin (\alpha + \beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha\)也是一个很重要的共识

（偷图我们最擅长了）

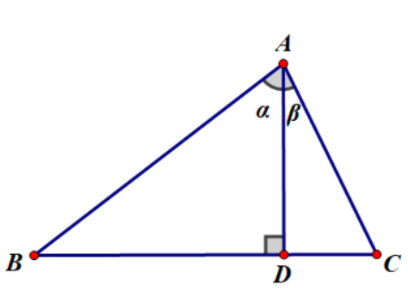
我们不难发现\(S_{\triangle ABC} = S_{\triangle ABD} = S_{\triangle ADC}\)

再根据上面推的三角形面积公式：

\[\frac{AB \times AC \times \sin (\alpha + \beta)}{2} = \frac{AB \times AD \times \sin \alpha}{2} + \frac{AD \times AC \times \sin \beta}{2}\\ AB \times AC \times \sin (\alpha + \beta) = AD \times (AB \times \sin \alpha + AC \times \sin \beta)\\ AD = \cos \alpha \times AB = \cos \beta \times AC \qquad \therefore AB = \frac{AD}{\cos \alpha}, AC = \frac{AC}{\cos \beta}\\ \therefore \frac{AD^2}{\cos \alpha \cos \beta} \times \sin(\alpha + \beta) = AD \times(\frac{AD \times \sin \alpha}{\cos \alpha} + \frac{AD \times \sin \beta}{\cos \beta})\\ \frac{\sin (\alpha + \beta)}{\cos \alpha \cos \beta} = \frac{\sin \alpha}{\cos \alpha} + \frac{\sin \beta}{\cos \beta} = \frac{\sin \alpha \cos \beta + \sin \beta \cos \alpha}{\cos \alpha \cos \beta}\\ \therefore \sin (\alpha + \beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha \]

余弦

(这图有点小)

作单位圆\(\circ O\)交\(x\)正半轴于\(A\),作\(\angle POA = \alpha\), \(\angle ROA = -\beta\)连接\(PR\) ,将\(\triangle POR\)绕点\(O\)旋转\(\beta\)至\(\triangle AOQ\)

则\(A(1, 0),\)\(P(\cos \alpha, \sin \alpha)\), \(R(\cos(-\beta) = \cos \beta, \sin (-beta) = -\sin \beta)\), \(\angle AOQ = \alpha + \beta\), \(Q(\cos(\alpha + \beta), \sin(\alpha + \beta))\)

因为旋转所以\(|QA| = |PR|, QA ^ 2 = PR^ 2\)

\[[\cos(\alpha + \beta) - 1]^2 + \sin^2(\alpha + \beta) = [\cos \alpha - \cos(-\beta)]^2 + [\sin \alpha - \sin(-\beta)]^2\\ cos^2(\alpha + \beta) + 1 - 2\cos(\alpha + \beta) + \sin^2(\alpha + \beta) = \cos^2 \alpha + \cos^2 \beta - 2\cos \alpha \cos \beta + \sin^2\alpha + \sin^2\beta + 2\sin\alpha \sin \beta\\ [\cos^2(\alpha + \beta) + \sin^2(\alpha + \beta)] + 1 - 2\cos(\alpha + \beta) = (\sin \alpha + cos\alpha) + (\sin \beta + \cos \beta) - 2 \cos \alpha \cos \beta + 2 \sin \alpha \sin \beta\\ \therefore 1 + 1 - 2\cos(\alpha + \beta) = 1 + 1 - 2(cos\alpha\cos\beta-\sin\alpha\sin\beta)\\ \therefore cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \]

这些和角公式都要记住……后面推出来有用的……

复数

向量

我们经常学的应该叫做标量。

有大小没有方向

比如说质量，体积。

但是我们也接触过一些有方向有大小的量

他们叫做矢量。

比如说力，速度。

注：数学里面计算的那个应该叫做速率？

向量也叫矢量，在二维及以上维度既有大小又有方向的量为矢量（矢量定义）

矢量可以用一个点指向另一个点的箭头表示。

一个平面向量也可以用一个数对\((x, y)\)表示，表示这个向量从\((0, 0)\)指向\((x, y)\)

当然向量不知平面向量，今天我们的FFT只用二维向量就可以了。所以我们只关注二维向量。

两个向量相等，当且仅当他们的方向，大小都相等。所以起点不是\((0, 0)\)的矢量也可以用数对表示，把他平移到起点为\((0, 0)\)就可以表示了

向量和常数（标量）相乘，大小相乘，方向不变。

所以\(\vec a // \vec b \Leftrightarrow \exist \lambda, \text{使得} \vec b = \lambda \vec a\)

向量的模

\(|\vec a|\)就是取\(\vec a\)的长度……说完了

向量加法

向量加法满足平行四边形法则和三角形法则

三角形法则

（图太难画我就不画了）

假设有三个点：饭堂，学校，考场。

\(\vec a\)从学校指向饭堂，\(\vec b\)从饭堂指向考场， \(\vec c\)从学校指向考场

\(\vec a + \vec b\)意味着你先从学校出发，去吃了个饭，然后去慷慨赴死考试

不看过程的话，其实你就是从学校出发去了考场。中途经过了什么地方没有半毛钱关系……

所以\(\vec a + \vec b = \vec c\)

(等于你没吃饭就上去了)

平行四边形法则

我们可以发现三角形法则的适用范围

当矢量\(\vec a\) 和 \(\vec b\)首尾相接的时候才能用

但是阴险狡诈的出题人怎么可能会让你有首尾相接的矢量

现在我们重新定义三个矢量

\(\vec a\)表示向北偏东37°方向走37米，\(\vec b\)表示向正东走4米

那么\(\vec a + \vec b\),就执行这两个指令就可以了……

设\(\vec a + \vec b = \vec c\)， 那么\(\vec c\)指向的点应该就是向北偏东37°走37米，再向东走4米的那个点。

因为先走\(\vec a\)再走\(\vec b\)和先走\(\vec b\)再走\(\vec a\)没有区别……

所以\(\vec a + \vec b = \vec b + \vec a\)

好了回到正题。

向量平移是不会改变大小和方向的

所以我们可以把\(\vec a\) 平移一下。

使得$\vec b $ 和 \(\vec {a'}\)首尾相接

这个时候如果我们把\(\vec a\) 和 \(\vec {a'}\)的终点连接起来……其实就是一个平行四边形

而\(\vec c\)就是平行四边形的一条对角线。

搬运某大佬的图：

矢量乘法

数乘

也叫标量乘法，是矢量和标量相乘

就是多走几个矢量而已……方向不变，长度相乘，前面讲过了。

这里注意，\(\vec b = \lambda \vec a\), \(\lambda = 0\)时 \(\vec b\)是零向量，零向量没有方向。 \(\lambda = 1\)时\(\vec b = \vec a\)， \(\lambda = -1\)时$\vec b $ 和 \(\vec a\)互为反向量

数量积

也叫点积，是向量和向量的乘积。这里注意符号要用点乘，不能用叉乘

\(\vec a \cdot \vec b = |\vec a| |\vec b| \cos \theta\)

\(\theta\)为向量\(\vec a\) 和 \(\vec b\)的夹角

当然这个也可以是\(\vec a\)在\(\vec b\)方向上的投影长度。这个是后话……

注意点乘出来的是标量，比如说物理中的做功就是用力的向量乘位移的向量，\(W = \vec F \cdot \vec s\)

向量积

不说了，怕你们混淆。

（其实我也混淆了）

有兴趣的小伙伴自行百度~

复数

是时候回到我们的复数了

虚数

初中老师是不是告诉你们没有\(\sqrt[2]{-1}\)这东西？

但是高中老师会告诉你们有，而且这东西还很重要

定义虚数单位\(i\)， \(i^2 = -1\)

那么\(i\)是多少？\(i = \sqrt[2]{-1}\)

初中有没有学过化简二次根式？

\(\sqrt[2]{a^2b} = a\sqrt[2]{b}\)

那么我们也可以推出\(\sqrt[2]{-7} = \sqrt[2]{-1 \times 7} = \sqrt[2]{7i^2} = \sqrt[2]{7}i\)

这样就变成了一个实数和\(i\)相乘

当然，\(i\), \(\sqrt[2]{-7}\)这种东西，在数轴上面是表示不出来的

所以相对应的，我们把它叫做虚数

\(\sqrt[2]{-1}\)就是虚数单位

复数

（有没有发现标题里面复数就有好多个……）

类似于有理数可以和无理数相加，实数也可以和虚数相加

\(18 + \sqrt[2]{-4} = 18 + 2i\)

类似于这样的数就叫做复数。

而且Python/C++里面好像有复数这一概念……

#include <complex>

是可以编译通过的……

x = 18 + 4j
print (type(x))

你会发现它输出了

<class 'complex'>

当然Python里面的虚数单位叫做j……（我也不知道为啥蒙了好久）

共轭复数

相信我，轭念（e4）

共轭复数，指两个实部相等，虚部互为相反数的复数互为共轭复数。

如\(3 + 2i\) 和 \(3 - 2i\)就是共轭复数

特别的，\(3 (+ 0i)\) 和\(3 (- 0i)\)（就是和自己）互为共轭复数

复数\(z\)的共轭复数记作\(\overline z\)

容易得到\(z \times \overline z = (x + yi)(x - yi) = x^2 - y^2i^2 = x^2 + y^2\)

容易得到共轭复数关于实轴对称

复平面

不难发现，对于一个复数\(z = a + bi\)

只要确定了\(a,b\)就确定以唯一的复数\(z\)

这就和平面直角坐标系上确定\((x, y)\)就可以确定一个点\(A(x, y)\)非常像

所以我们整一个复平面：

在复平面内，\(x\)轴上的点都表示实数，\(y\)轴除了原点之外都是纯虚数。

所以一般把\(x\)成为实轴， \(y\)称为虚轴

点\(Z(a, b)\)就可以表示复数\(z = a + bi\)

然后我们发现，\(Z(a, b)\)也可以表示向量\(\vec{OZ}\)

所以复数\(z = a + bi\)也可以用向量\(\vec{OZ}\)来表示

模长

复数的模……和向量的模差不多

\(\vec{OZ}\)的长度就是\(|\vec {OZ}| = |z|\)

不难发现\(|a + bi| = \sqrt[2]{a^2+b^2}\)

辐角

当\(z \neq 0\)的时候，向量\(\vec {OZ}\) 和 \(x\)的夹角就叫做辐角。

当然也可以理解为以\(OZ\)为终边的角的度数

这里注意一下区分正角和负角

有了辐角和模长，我们就可以表示一个向量了。

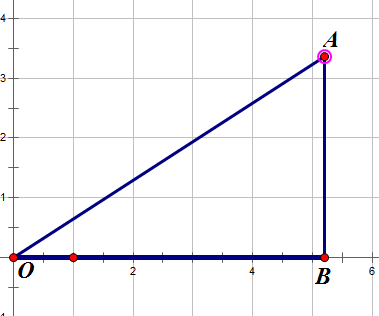
设\(|\vec {OA}| = r, \angle AOB = \theta\),根据三角函数，\(AB = r \times \sin \theta\), \(OB = r \times \cos\theta\)

根据三角形法则，\(\vec{OA} = \vec {OB} + \vec {BA} = r \times \cos \theta + r \times \sin \theta \times i\)

化简一下，若\(\vec a\)的模长为\(|\vec a|\), 辐角为\(\theta\)，则\(\vec a = r(\cos \theta + i \times \sin \theta )\)

同样滴，\(\vec a\)对应的复数\(A\) 也可以用模长和辐角表示

复数乘法

矢量乘法我们没讲过……\(qwq\)

但是复数是可以相乘的

因为他们是数。

我们可以用乘法分配律

设复数\(A,B\), \(A = a + bi\), \(b = c + di\)

\[A \times B = (a + bi) \times (c + di) = ac + adi + bci + bdi^2\\ =ac + adi + bci - bd = (ac - bd) + (bc + ad)i \]

这是用普通方法表示

那么用模长和辐角表示呢？

设复数\(A, B\), \(A = r_A (\cos \theta_A + \sin \theta_Ai), B = r_B(\cos \theta_B + \sin \theta_Bi)\)

(前方高能)

\[A \times B = r_A r_B \times (\cos \theta_A + \sin \theta_Ai)(\cos \theta_B + \sin \theta_Bi)\\ = r_A r_B \times(\cos \theta_A \cos \theta_B + i\times \sin\ \theta_A \cos \theta_B + i \times \sin \theta_B \cos \theta_A + \sin\theta_A \sin \theta_B \times i^2)\\ = r_A r_B \times\left[\cos\theta_A \cos \theta_B - \sin \theta_A\sin\theta_B + (\sin \theta_B\cos\theta_A + \sin \theta_A \cos \theta_B)i\right]\\ =r_a r_B \times(\cos(\theta_A + \theta_B) + \sin(\theta_A + \theta_B)i) \]

(根据三角函数和角公式，上面应该有，没有就去百度去)
所以两个复数相乘的结果就是：模长相乘，辐角相加

单位根

在复平面内，其中一个顶点为\(1(+0i)\)正\(n\)边型的所有顶点称为\(n\)次单位根。

特别的，\(1\)次单位根为\(1\), \(2\)次单位根为\(\pm1\)

看一下百度百科给的定义

数学上，n次单位根是n次幂为1的复数。它们位于复平面的单位圆上，构成正n边形的顶点，其中一个顶点是1。

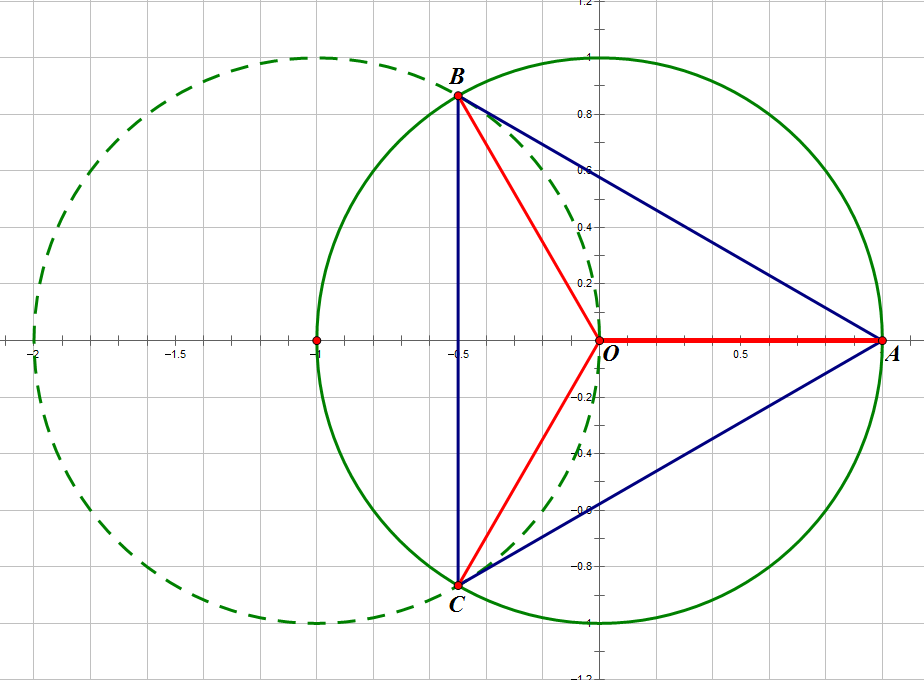
如图，\(\triangle ABC\)是正三角形就不证了……

这里\(\circ O\)是单位圆，\(A(1, 0)\)，那么\(\vec {OA}, \vec {OB}, \vec {OC}\)表示的复数都是三次单位根。

类似的，你也可以求出其他单位根……

我们来研究一下\(n\)次单位根有什么性质

用数学方法，我们可以求出\(A = 1\), \(B = -0.5 + \frac{\sqrt[2]{3}}{2}i\), \(C = -0.5 - \frac{\sqrt[2]{3}}{2}i\)

这样我们试验了很多性质，发现好像都不太对……

就差\(A^n, B^n, C^n\)没有试了……

但是写成和的形式……您慢慢拆吧……

我们把它写成模长和辐角表示的形式

我们来回忆一下一个向量怎么写成这种形式

化简一下，若\(\vec a\)的模长为\(|\vec a|\), 辐角为\(\theta\)，则\(\vec a = r(\cos \theta + i \times \sin \theta )\)（不错我就是复制的）

设\(A\)是单位圆和实轴的交点，\(B\)是辐角为正且最小的单位根，\(C\)是辐角为负且最小的单位根。

这里注意\(C\)的辐角最小指大小，和符号没有关系

\(A = 1 \times (\cos \angle AOA + i\sin \angle AOA)\)

\(B = 1 \times (\cos \angle AOB + i \sin \angle AOB)\)

\(C = 1 \times (\cos \angle AOC + i \sin \angle AOC)\)注意这里$\angle AOC $应该是一个负角

根据模长相乘，辐角相加，可得

\(A^n = 1^n \times [\cos (n \angle AOA) + i \sin (n \angle AOA)]\)

\(B^n = 1^n \times [\cos(n\angle AOB) + i \sin(n\angle AOB)]\)

\(C^n = 1^n \times [\cos (n\angle AOC) + i \sin (n \angle AOC)]\)

我们再看一下单位根的定义，是正\(n\)边形的定点。

那么在正多边形中，中心角该都是相等的。

PS：正多边形的外接圆(或内切圆)的圆心叫做正多边形的中心，外接圆的半径叫做正多边形的半径，内切圆的半径叫做正多边形的边心距．正多边形各边所对的外接圆的圆心角都相等．正多边形每一边所对的外接圆的圆心角叫做正多边形的中心角．正n边形的每个中心角都等于360°/n

也就是\(\angle AOB = - \angle AOC = \frac{2 \pi (rad)}{n}\)

那么\(n\angle AOB = 2\pi = 360 = 0, n \angle AOC = -2\pi = 0\)

然后\(\sin 0 = 0, \cos 0 = 1\)

所以\(A^n = B^n = C^n = 1\)

那么推广一下，如果是任意一个单位根呢？

我们先设辐角最小且为正的向量对应的单位根为\(\omega_n^1\)

因为中心角相等，所以第二个单位根的辐角就是第一个单位根的两倍，模长相乘之后还是1，

因此，我们就可以用\(\omega_n^1 \times \omega_n^1 = \omega_n^2\)表示第二个\(n\)次单位根。

同样滴，我们可以用\(\omega_n^i (0 \leq i \leq n)\)表示第\(i\)个\(n\)次单位根。

注意\(\omega_n^0 = \omega_n^n = 1\)

又因为中心角相等，所以\(\omega_n^i\)的辐角就应该是\(i \times \frac{2\pi}{n}\)

模长是1

所以\(w_n^i = 1^i \times (\cos \frac{2\pi i}{n} + i \sin \frac{2\pi i}{n})\)

然后\((\omega_n^i)^n = {1^i}^n \times [\cos (\frac{2\pi i}{n} \times n) + i \sin (\frac{2\pi i}{n} \times n)] = \cos 2\pi i + \sin 2\pi i = \cos 2\pi + \sin 2\pi = \cos 0 + \sin 0 = 1\)

所以单位根的定义就是:\(\left \{ z | z ^ n = 1\right \}, n \in \N^*\)
(就是所有正整数次幂能达到1的复数)

性质

• \(\omega_n^k = \cos \frac{2\pi k}{n} + i \sin \frac{2 \pi k}{n}\),这个上面讲过不说了。
• \(\omega_{2n}^{2k} = \omega_n^k\)
  感性理解：\(\omega_{2n}^{2k}\)把圆分成\(2n\)份，取了\(2k\)份，就是一整个圆的\(\frac{2k}{2n} = \frac{k}{n}\) \(\omega _n ^k\)把圆分成\(n\)份，取了\(k\)份，就是一整个圆的\(\frac{k}{n}\)
  理性分析：\(\omega_{2n}^{2k} = \cos \frac{2\pi \times 2k}{2n} + i\sin \frac{2\pi \times 2k}{2n} = \cos \frac{2 \pi k}{n} + i \cos \frac{2 \pi k}{n} = \omega _n ^ k\)
• \(\omega_n^{k + \frac{n}{2}} = - \omega_n^k\)
  感性理解：多转了半圈，关于原点对称，实部和虚部都要取反。
  理性分析：\(\omega_n^{\frac{n}{2}} = \cos \frac{2 \pi \frac{n}{2}}{n} + i \sin \frac{2 \pi \frac{n}{2}}{n} = \cos \frac{\pi n}{n} + i \sin \frac{\pi n}{n} = \cos \pi + i \sin \pi = -1 + 0 = -1\);
  \(\omega_n^k \times \omega_n^{\frac{n}{2}} = \omega _n^{k + \frac{n}{2}}\),这个是同底数幂相乘……前面说过的
  代入$\omega_n^{\frac{n}{2}} = -1 $ 得到 \(- \omega_n^k = \omega_n^{k + \frac{n}{2}}\)
• \(\omega_n^0 = \omega_n^n = 1\)

---

好了前方高能，进入正题。

2. 快速傅里叶变换(FFT)

*注：看不懂的可以坚持看下去，或许看到后面你就懂了呢？

讲完了前置知识是不是很开心

那么我们讲单位根是干嘛的呢

如果我们设\(x = \omega_n^1\)，那么\(x^2\)就是第二个\(n\)次单位根，\(x^3\)就是第三个\(n\)次单位根……

然后我们就可以用单位根表示一个多项式。

两个多项式相乘……就是单位根相乘……

（好像挺快的）

（看下去再说吧）

为了方便讨论，下文默认\(n\)为\(2\)的整数次幂

前面我们提到过，一个\(n\)次多项式可以被\(n + 1\)个点唯一确定

这些点\(a_i (0 \leq i \leq n)\)就是\(i\)次项系数

我们设\(x\)的\(n\)次多项式\(f(x) = \{a_i|0\leq i \leq n - 1\}\)

那么\(f(x)\)的值就应该是\(f(x) = \displaystyle \sum_{i = 0}^{n - 1} a_ix^i\)

按照次数的奇偶性分类一下\(f(x) = \displaystyle \sum _{i = 0}^{\frac{n - 2}{2}}a_{2i}x^{2i} + \sum_{i = 0}^{\frac{n - 2}{2}}a_{2i + 1}x^{2i + 1}\)

注意这里的\(i\)不是虚数单位，不要混淆了。

如果我们设\(f_1(x) = \displaystyle \sum_{i = 0}^{\frac{n - 2}{2}}a_{2i}x^{i} = a_0 + a_2x + a_4x^2 + \cdots + a_{n - 2}x^{\frac{n - 2}{2}}\)

如果我们设\(f_2(x) = \displaystyle \sum _{i = 0} ^ {\frac{n - 2}{2}}a_{2i + 1}x^i = a_1 + a_3x + a_5x^2 + \cdots + a_{n - 1}x^\frac{n - 2}{2}\)

我们能不能用\(f_1, f_2\)表示出\(f\)呢？

肯定是可以的
\(f_1\)包含了所有系数下标为偶数的单项式，\(f_2\)包含了所有系数下标为奇数的单项式。

我们可以把\(x\)的指数扩大到和系数的下标一样

观察\(f_1\)，每个系数的下标都是指数的两倍，考虑代入\(x^2\)

会有\(f_1(x^2) = a_0x^0 + a_2x^2 + a^4x^4 + \cdots + a_{n - 2} x^{n - 2}\)

同样的，\(f_2(x^2) = a_1x^0 + a^3x^2 + \cdots + a_{n - 1}x^{n - 2}\)

还差了1咋办？

给他乘上呗~

\(x\times f_2(x^2) = a_1x^1 + a_3x^3 + \cdots + a_{n - 1}x^{n- 1}\)

根据前置知识里面的加法，可以得到\(f_1(x^2) + xf_2(x^2) = f(x)\)

根据前文，我们把单位根代入回来。

当然那么多单位根，为了确保普遍性，我们代入\(\omega_n^k\)，\(k\)的取值我就不多说了……

\[f(\omega_n^k) = f_1(\omega_n^{2k}) + \omega_n^kf_2(\omega_n^{2k}) \tag{1} \]

没了？怎么可能

还记不记得我们有一条公式\(\omega_n^{k + \frac{n}{2}} = - \omega_n^k\)

如果\(k < \frac{n}{2}\),也就是\(k + \frac{n}{2} < n\),那么我们也可以有

\[f(\omega_n^{k + \frac{n}{2}}) = f_1\left(\omega_{n}^{2 \times\left(k + \frac{n}{2}\right)}\right) + \omega_{n}^{k + \frac{n}{2}}f_2\left(\omega_n^{2\times\left(k+\frac{n}{2}\right)}\right) = f_1(\omega_n^{2k + n}) + (-\omega_n^k)f_2(\omega_n^{2k + n})\\ =f_1(\omega_n^{2k} \times \omega_n^n) - \omega_n^kf_2(\omega_n^{2k}\times\omega_n^n)\\ = f_1(\omega_n^{2k})- \omega_n^kf_2(w_n^{2k}) \tag{2} \]

对比一下式子\((1)\) 和 \((2)\) （编号在最右边）

不难发现， 对于确定的 \(\omega_n^{k}\), \(f(\omega_n^k)\) 和 \(f(\omega_n^{k + \frac{n}{2}})\)\((k <\frac{n}{2})\)只有一个常数项 \(\omega_n^kf_2(\omega_n^{2k})\) 的符号不同……

所以我们在使用一些花里胡哨的算法枚举\(f(\omega_n^k)\), 也就是计算\(f_1(\omega_n^{2k})\) 和 \(\omega_n^kf_2(w_n^{2k})\)的时候，也可以用\(O(1)\)的复杂度求出\(f\left(\omega_n^{k + \frac{n}{2}}\right)\)

这里\(k\)的取值范围是\(0 \leq k<\frac{n}{2}\),那么\(\frac{n}{2} \leq k + \frac{n}{2} < n\)

尝试把小于号变成小于等于。

\(0 \leq k < \frac{n}{2}, \frac{n}{2} \leq k + \frac{n}{2} \leq n - 1\)

这就意味着我们只需要求\(f(\omega_n^i) (0 \leq i < \frac{n}{2})\)就可以求出\(f(\omega_n^j)(0\leq j \leq n - 1)\)

这样我们就通过二分把问题缩小了一半

然后我们发现，我们要求的\(f(\omega_n^i) (0 \leq i < \frac{n}{2})\)也可以用二分

也就是说我们可以递归下去……

递归边界就是当\(i = 0\)的时候，多项式只剩下一个常数项，直接返回就好了

所以FFT相当于二分过程……时间复杂度是\(O(n\log n)\)

3. 快速傅里叶逆变换(IFFT)

但是我们FFT求出来的东西

能直接输出吗？

我们平时是很少用复数来表示一个多项式的……

我们借助一个偏门的方法，快速求出了多项式。

结果发现结果你看不懂……

那有啥用？

所以我们要通过快速傅里叶变换的逆变换把多项式转换回来。

前方高能

听不懂的没关系，把结果记下来也可以愉快地写IFFT，反正我也没听懂

假设我们现在通过FFT得到了一些点值\(\{y_i|0\leq i \leq n - 1\}\), 我们要把它变换回多项式系数\(\{a_i|0\leq i \leq n - 1\}\)

设有向量\(c_i(0\leq i \leq n - 1)\)满足

\[c_k = \displaystyle \sum_{i = 0}^{n - 1} y_i(\omega_n^{-k})^i \]

好像又到了抄推公式的时间……

\[\displaystyle c_k = \sum_{i = 0}^{n - 1} y_i(\omega_n^{-k})^i = \sum_{i = 0}^{n - 1}\left[\sum_{j = 0}^{n- 1}a_j\left(\omega_n^i\right)^j\left(\omega_n^{-k}\right)^i\right]\\ =\sum_{i = 0}^{n - 1}\left[\sum_{j = 0}^{n- 1}a_j\left(\omega_n^j\right)^i\left(\omega_n^{-k}\right)^i\right]\\ = \sum_{i = 0}^{n - 1}\left[\sum_{j = 0}^{n- 1}a_j\left(\omega_n^{ij}\right)\left(\omega_n^{-ik}\right)\right]\\ =\sum_{i = 0}^{n - 1}\left[\sum_{j = 0}^{n- 1}a_j\left(\omega_n^{ij - ik}\right)\right]\\ =\sum_{i = 0}^{n - 1}\left[\sum_{j = 0}^{n- 1}a_j\left(\omega_n^{j - k}\right)^i\right]\\ =\sum_{i = 0}^{n - 1}\sum_{j = 0}^{n- 1}a_j\left(\omega_n^{j - k}\right)^i\\ = \sum_{j = 0}^{n - 1}a_j\left[\sum_{i = 0}^{n - 1}\left(\omega_n^{j - k}\right)^i\right] \tag{3} \]

我们设有数列\(A = {x^0, x^1, \cdots, x^{n - 1}}\)，不难发现则是一个等比数列，公比为\(x\)

那么这个等比数列的和\(S(x)\)就是

\[\displaystyle S(x) = \sum_{i = 0}^{n - 1} x^i\\ xS(x) = \sum_{i = 1}^nx^i\\ xS(x) - S(x) = (x - 1) S(x) = x^n - x^0\\ \therefore S(x) = \frac{x^n - 1}{x - 1} \]

如果，这个数列的公比是\(\omega_n^k\)

那么

\[S\left(\omega_n^k\right) = \frac{(\omega_n^k)^n - 1}{\omega_n^k - 1} = \frac{\omega_n^{kn}}{\omega_n^k - 1} = \frac{(\omega_n^n)^k - 1}{\omega_n^k - 1} = \frac{1^k - 1}{\omega_n^k - 1} = \frac{0}{\omega_n^k - 1} \]

这里\(\omega_n^k - 1\)是分母不\(0\)

所以当\(\omega_n^k\)为\(1\)的时候需要特别讨论

\(\omega_n^k\)是\(1\),就说明这个数列的公比是\(1\),而且\(k = 0\)或\(k = n\)

那么很清楚了吧？这个时候\(S(\omega_n^k) = S(1) = nx^0 = n\)

很明显，\(S\left(\omega_n^k\right) = \sum_{i = 0}^{n - 1}\omega_{n}^{i} = 0\)

考虑回前面的式子\((3)\)

\[c_k = \sum_{j = 0}^{n - 1}a_j\left[\sum_{i = 0}^{n - 1}\left(\omega_n^{j - k}\right)^i\right] \tag{3} \]

里面有一个\(\sum_{i = 0}^{n - 1}\left(\omega_n^{j - k}\right)^i \tag4\)

根据上面讨论的结果，如果\(j - k = 0\) 或者\(j - k =n\)的时候，\((4)\)的结果是\(n\),否则就是\(0\)

当然， 这里\(j\leq n - 1, k \geq 0, \therefore j - k < n - 1 < n\)，所以\(j - k =0, j = k\)

代入式子\((3)\)

\[\displaystyle c_k = \sum_{j = 0}^{n - 1}\left(a_j \times \begin{cases} 0 & j \neq k\\ n & j = k \end{cases} \right) \]

因为我们知道\(0\leq k\leq n - 1, 0\leq j \leq n - 1\),所以在求和枚举的过程中，\(\exist! j = k\)

因为只有当\(j = k\)的时候这个单项式才是\(na_k\),其他时候都是\(0\),

所以我们就得出了：

\[c_k = na_k\\ a_k = \frac{c_k}{n} \]

根据这个，就可以用IFFT把点转回系数

然后就会有人（我）问

这个\(c_k\)怎么求呢？

我们观察一下它的定义式

\[c_k = \displaystyle \sum_{i = 0}^{n - 1}y_i(\omega_n^{-k})^i\\ =\left(\sum_{i = 0}^{n - 1}y_i\right) \times \left[\sum_{i = 0}^{n - 1}(\omega_n^{-i})^k \right]\\ =\left(\sum_{i = 0}^{n - 1}y_i\right) \times \left[\sum_{i = 0}^{n - 1}(\omega_n^{n-i})^k \right]\\ \]

可以发现，对于每一个\(c_k\)，前面的乘数都是一个固定的常数

只要求后半部分就可以了

---

总结一下

一张图总结（引用一下远航之曲大佬的图）

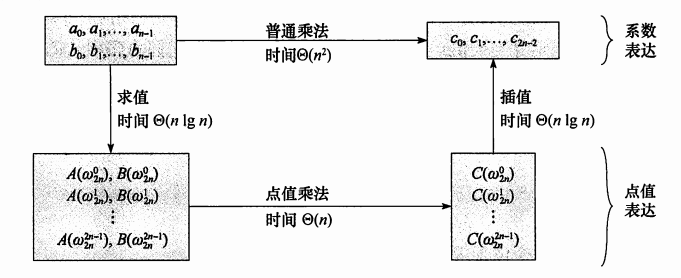
诶诶诶别走啊

不看完你知道怎么写代码吗？

不知道怎么写代码学这么多干嘛？

代码实现

递归实现

按照上面说的方法，二分过程求\(f(\omega_n^i)\)

我可以直接贴代码了！

（好了忘给题目了……）传送门

这里提醒一下，虽然C++有complex库，但还是推荐手写吧……花不了多久的……

还有就是\(acos(-1.0) = \pi(rad)\)

数组的话……需要开大一点

具体多大呢？看完代码我们再来推一下

#include <cmath>
#include <string>
#include <cstdio>
#include <cstring>
using std::memset;
const int mod = 998244353;
// #define Cdebug

const double Pi = acos(-1.0);
class complex
{
private:

public:
    complex(const double _real = 0, const double _image = 0) : real(_real), image(_image) {};
    virtual ~complex() {}
    inline double get_real() const { return real; }
    inline double get_image() const { return image; }
    inline void set_real(const double& _real) { real = _real; }
    inline void set_image(const double& _image) { image = _image; }
    complex operator = (const complex&);
    friend const complex operator + (const complex&, const complex&);
    friend const complex operator - (const complex&, const complex&);
    friend const complex operator * (const complex&, const complex&);
    #ifdef Cdebug
    void print();
    #endif // Cdebug
protected:
    double real, image;
};

template <typename T>
const T read()
{
    int x = 0;
    char ch = getchar();
    while(ch < '0' or ch > '9')
    {
        ch = getchar();
    }
    while(ch >= '0' and ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch ^ 48);
        ch = getchar();
    }
    return x;
}

template <typename T>
void read(T& x)
{
    x = 0;
    char ch = getchar();
    while(ch < '0' or ch > '9')
    {
        ch = getchar();
    }
    while(ch >= '0' and ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch ^ 48);
        ch = getchar();
    }
}

template <typename T>
void write(const T x)
{
    if(x < 0)
    {
        putchar('-');
        if(x > 9) write(x / 10);
        putchar(x % 10 + 48);
    }else
    {
        if(x > 9) write(x / 10);
        putchar(x % 10 + 48);
    }
}

void FFT(int, complex[], const double = 1.0);

complex a[2097153], b[2097153];
int n, m, limit;
int main()
{
    read(n);
    read(m);
    for(register int i = 0; i <= n; i++) a[i].set_real(read<int>());
    for(register int i = 0; i <= m; i++) b[i].set_real(read<int>());
    limit = 1;
    while(limit <= n + m) limit <<= 1;
    FFT(limit, a);
    FFT(limit, b);
    for(register int i = 0; i <= limit; i++)
        a[i] = a[i] * b[i];
    FFT(limit, a, -1);
    for(int i = 0; i <= n + m; i++)
    {
        #ifdef Cdebug
        a[i].print();
        putchar(10);
        #endif // Cdebug
        printf("%d ", (int)(a[i].get_real() / limit + 0.5) % mod);
    }
    return 0;
}

complex complex::operator = (const complex& a)
{
    this -> real = a.real;
    this -> image = a.image;
    return *this;
}

const complex operator + (const complex& a, const complex& b)
{
    return complex(a.real + b.real, a.image + b.image);
}

const complex operator - (const complex& a, const complex& b)
{
    return complex(a.real - b.real, a.image - b.image);
}

const complex operator * (const complex& a, const complex& b)
{
    return complex(a.real * b.real - a.image * b.image,
                   a.image * b.real + a.real * b.image);
}

void FFT(int limit, complex a[], const double I)
{
    if(limit == 1) return ;
    #ifdef Cdebug
    for(register int i = 0; i <= limit; i++)
    {
        printf("a%d:", i); a[i].print();
        putchar(10);
    }
    #endif // Cdebug
    complex a1[(limit >> 1) + 1], a2[(limit >> 1) + 1];
    for(register int i = 0; i <= limit; i += 2)
    {
        a1[i >> 1] = a[i];
        a2[i >> 1] = a[i + 1];
    }
    FFT(limit >> 1, a1, I);
    FFT(limit >> 1, a2, I);
    register const complex omega(cos(2.0 * Pi / limit), I * sin(2.0 * Pi / limit));
    register complex root(1, 0);
    register const int limits = limit >> 1;
    for(register int i = 0; i < limits; i++, root = root * omega)
    {
        a[i] = a1[i] + root * a2[i];
        a[i + limits] = a1[i] - root * a2[i];
    }
    return ;
}

#ifdef Cdebug
void complex::print()
{
    printf("real:%lf image:%lf %lf", real, image, real / limit);
}
#endif // Cdebug

我们看见洛谷的数据范围\(1 \leq n, m, \leq 10^6\)

我们要发扬卡空间的优良传统，开数组最多只开大一个

是不是以为开到\(10^6 + 1\)就够了？

这是开到了\(10^6+20\)的：

事实上，开到\(3 \times 10^6\)是可以满分的

但是我们来卡一下空间

看一下主函数里面的这句：

while(limit <= n + m) limit <<= 1;

结合一下数据范围：\(n + m \leq 2 \times 10 ^6\)

那么limit最大取到多少呢？

\(\log_22000000 = 20.0+\)

所以limit最大会取到\(2^{21} = 2097152\)

观察代码，我们会发现limit就是数组下标上限

所以我们的数组开到\(2097153\)就可以精准卡空间。

迭代优化

以为这就完了？

都不知道谁想出来的迭代优化。

我们知道我们二分的过程中是按照数组下标的奇偶性来分类的

那么我们来画一张二分的图，观察一下下标的二进制

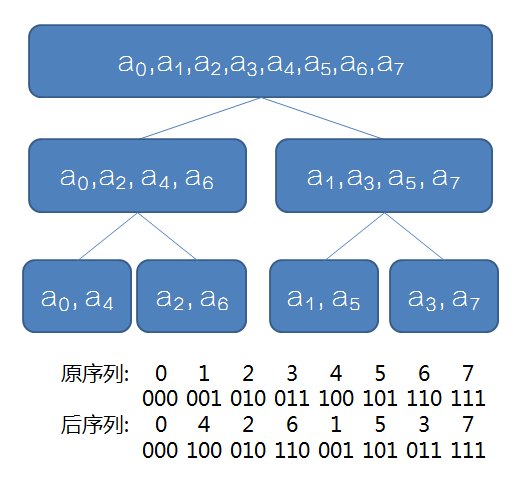
有没有发现，后序列每一个数的二进制就是原序列每一个数的二进制反转

设\(A = {A_0, A_1,\dots,A_n}, n = 2^k - 1, k \in \N^*\)为原序列，\(B = B_0, B_1, \dots, B_n, n = 2^k\)为后序列易得\(A_0 = 0, B_0 = 0\)

那么我们知道\(A\)的通项公式：\(A_i = i\)因为原序列就是按顺序的下标。

所以\(A_1 = 1 = (\overline {\underbrace{0\dots 0}\limits_{k - 1个0}1})_2\),根据规律，\(B_1 = (\overline {1\underbrace{0\dots 0}\limits_{k - 1个0}})_2\)

目前还发现不了什么规律，我们继续看下去

\[A_0 = (\underbrace{0\dots0}\limits_{k个0})_2 \qquad B_0 = (\underbrace{0\dots0}\limits_{k个0})_2\\ A_1 = (\underbrace{0\dots0}\limits_{k - 1个0}1)_2 \qquad B_1 = (1\underbrace{0\dots0}\limits_{k - 1个0})_2\\ A_2 = (\underbrace{0\dots0}\limits_{k - 2个0}10)_2 \qquad B_2 = (01\underbrace{0\dots0}\limits_{k - 2个0})_2\\ A_3 = (\underbrace{0\dots0}\limits_{k - 2个0}11)_2 \qquad B_3 = (11\underbrace{0\dots0}\limits_{k - 2个0})_2\\ A_4 = (\underbrace{0\dots0}\limits_{k - 3个0}100)_2 \qquad B_4 = (001\underbrace{0\dots0}\limits_{k - 3个0})_2\\ A_5 = (\underbrace{0\dots0}\limits_{k - 3个0}101)_2 \qquad B_5 = (101\underbrace{0\dots0}\limits_{k - 3个0})_2\\ \cdots \]

发现规律没有？

没有

我们要求的是数列\(B\),但是\(B\) 和 \(A\)之间好像没有关系

那么如果我们单独研究序列\(B\)呢？

\[B_0 = (\underbrace{0\dots0}\limits_{k个0})_2\\ B_0 = (\underbrace{0\dots0}\limits_{k个0})_2 \qquad B_1 = (1\underbrace{0\dots0}\limits_{k - 1个0})_2\\ B_1 = (1\underbrace{0\dots0}\limits_{k - 1个0})_2 \qquad B_2 = (01\underbrace{0\dots0}\limits_{k - 2个0})_2 \quad B_3 = (11\underbrace{0\dots0}\limits_{k - 2个0})_2\\ B_2 = (01\underbrace{0\dots0}\limits_{k - 2个0})_2 \qquad B_4 = (001\underbrace{0\dots0}\limits_{k - 3个0})_2 \quad B_5 = (101\underbrace{0\dots0}\limits_{k - 3个0})_2\\ \cdots \]

观察一下\(B_i\) 和 \(B_{\lfloor\frac{i}{2}\rfloor}\)之间的关系

（我都把他们放在一行了）

首先我们要知道在C++中有右移运算符，a >> k相当于a整除\(2^k\)，而且也很形象，二进制下把所有数字向右移\(k\)位，最右边\(k\)位舍弃

所以整除2的整数次幂就直接二进制下右移就可以了

好了有了知识铺垫，我们发现，\(B_{2i}\) 和 \(B_{2i + 1}, i \in \N\)，只有最高位不同

\(B_{2i}\)的最高位是0， \(B_{2i + 1}\)的最高位是1

很好，距离规律很近了

再观察一下\(B_i\) 和 \(B_{2i}\)的区别

观察到\(B_{2i} = B_i >> 1\)

所以我们就得到了\(B\)的通项公式

\[B_i = \begin{cases} 0 & i = 0\\ \left\lfloor B_{\left\lfloor\frac{i}{2}\right\rfloor} / 2\right\rfloor + 2^{k - 1}\times(i \mod 2) & i > 0 \end{cases} \]

为什么大于0的时候后面要乘以\(i\)除\(2\)的余数呢？这是因为如果\(i\)是奇数，那么他的翻转的最高位就应该是\(1\)，否则就是\(0\)
所以我们就要加上这一句
写成代码就是
B[i]=(B[i>>1]>>1)|((i&1)<<(limit-1));
得到了\(B\),我们再根据

使用\(B\)不断向上合并，就可以得到结果了

那么我们有了原序列，怎么得到后序列呢

注意\(B\)是不能修改的，还要留着下次用，我们只能把\(A\)改成后序列

我们可以每次比较，如果\(A_i = i < B_i\),那么就交换\(A_i\) 和 \(A_{B_i}\)，这样就可以得到后序列了

详见代码：

#include <bits/stdc++.h>
using namespace std;

complex <double> a[2097153], b[2097153];
int n, m, limit, l, r[2097153];
double c;
const double Pi = acos(-1.0);

void FFT(const int, complex<double>[], const int = 1);

int main()
{
    scanf("%d%d", &n, &m);
    for(register int i = 0; i <= n; ++i)
    {
        scanf("%lf", &c);
        a[i].real(c);
    }
    for(register int i = 0; i <= m; ++i)
    {
        scanf("%lf", &c);
        b[i].real(c);
    }
    limit = 1;
    while(limit <= n + m) limit <<= 1, ++l;
    for(register int i = 1; i <= limit; ++i)
    {
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
    }
    FFT(limit, a);
    FFT(limit, b);
    for(register int i = 0; i <= limit; ++i) a[i] *= b[i];
    FFT(limit, a, -1);
    for(register int i = 0; i <= n + m; ++i)
    {
        printf("%d ", (int)(a[i].real() / limit + 0.5));
    }
    return 0;
}

void FFT(const int limit, complex<double> a[], const int flag)
{
    for(register int i = 0; i < limit; ++i)
    {
        if(i < r[i]) swap(a[i], a[r[i]]);
    }
    for(register int mid = 1; mid < limit; mid <<= 1)
    {
        // omega(cos(Pi * 2 / (mid * 2)), flag * sin(Pi * 2 / (mid * 2)))
        complex<double> root(cos(Pi / mid), flag * sin(Pi / mid));
        for(register int R = mid <<1, j = 0; j < limit; j += R)
        {
            complex<double> omega(1, 0);
            for(register int k = 0; k < mid; ++k, omega *= root)
            {
                complex<double> x = a[j + k], y = omega * a[j + mid + k];
                a[j + k] = x + y;
                a[j + mid + k] = x - y;
            }
        }
    }
}

补充：符号们

当然也要给你们一个目录可以快速回到之前读到的地方

目录

• 参考资料：快速傅里叶变换(FFT)详解 - 自为风月马前卒- 博客园
  • 0. 前言
  • 1. 前置知识
    • 加法
    • 乘法
    • 乘方
    • 开方
      • 算术平方根
    • 集合
      • 概念
      • 表示
      • 符号们
      • 特性
        • 确定性
        • 互异性
        • 无序性
      • 分类
        • 空集
        • 子集
        • 交集
        • 并集
        • 相对补集
        • 绝对补集
        • 幂集(好像不要求掌握)
        • 区间
        • 相等集合
      • 表示方法
        • 列举法
        • 描述法
        • 图像法
        • 符号法
    • 多项式
      • 系数表示法
      • 点值表示法
      • 简单介绍一下DFT和IDFT
    • 三角函数
      • 角
      • 象限角
      • 圆
        • 圆周角与圆心角
        • 角度的弧度制
      • 函数
        • 定义域
        • 值域
        • 对应法则
      • 反函数
      • 初中的三角函数
      • 任意角的三角函数
      • 诱导公式
      • 三角函数的反函数
      • 补：三角形的面积公式
      • 三角函数的和角公式
        • 正弦
        • 余弦
    • 复数
      • 向量
      • 向量的模
      • 向量加法
        • 三角形法则
        • 平行四边形法则
      • 矢量乘法
        • 数乘
        • 数量积
        • 向量积
      • 复数
        • 虚数
        • 复数
        • 共轭复数
      • 复平面
      • 模长
      • 辐角
      • 复数乘法

    • 单位根

      • 性质
  • 2. 快速傅里叶变换(FFT)
  • 3. 快速傅里叶逆变换(IFFT)
• 总结一下
• 代码实现
  • 递归实现
  • 迭代优化
• 补充：符号们
• 补充：快读快写

参考资料：还是百度百科

基本数学符号

符号种类	符号	名字	解说	例子	读作
逻辑符号	⇒	实质蕴含	A ⇒ B 意味着如果A为真，B也为真。如果A为假，则对B没有任何影响	x = 2 ⇒ x² = 4 为真，但 x² = 4 ⇒ x = 2 一般为假(因为 x 可以是 −2)。	蕴含；如果..那么
	→		可能意味着同 ⇒ 一样的意思(这个符号也可以指示函数的域和陪域；参见数学符号表)。
	⊃		可能意味着同 ⇒ 一样的意思(这个符号也可以指示超集)。
	⇔	实质等价	A ⇔ B 意味着 A 为真如果 B 为真，和 A 为假如果 B 为假。	x + 5 = y +2 ⇔ x + 3 = y	当且仅当,iff
	↔
	¬	逻辑否定	¬A 为真，当且仅当 A 为假。	¬(¬A) ⇔ A	非
	/	命题逻辑	穿过其他算符的斜线 等同于在它前面放置的"¬"。	x ≠ y ⇔ ¬(x = y)
	∧	逻辑合取	如果 A 与 B 二者都为真，则陈述 A ∧ B 为真；否则为假。	n < 4 ∧ n >2 ⇔ n = 3（当 n 是自 然数的时候）。	与
	∨	逻辑折取	如果 A 或 B有一个为真陈述 或二者均为真陈述，则 A ∨ B 为真；如果二者都为假，则 陈述为假。	n < 3 ∨ n > 3 ⇔ n ≠ 3	或
	⊕	xor	陈述 A ⊕ B 为真，当且仅当A, B真假性不同。A ⊻ B 意思相同。	(¬A) ⊕ A 总是真，A ⊕ A 总是假。	异或
	⊻
	∀	全称量词	∀x,P(x)为真，意味着对于所有存在的x，都有P(x)为真	∀ n, n² ∈ N（n ∈ R）	对于所有；对于任何；对于每个；任意的
	∃	存在量词	∃ x, P(x)为真,意味着存在至少一个x使P(x)为真。	∃ n ∈ N（n 是偶数）。	存在着
	∃!	唯一量词	∃! x,P(x),意味着精确的有一个x使P(x)为真。	∃! n ∈ N（n + 5 = 2n）	精确的存在一个
	:=	定义	x := y 或 x ≡ y 意味着 x 被定义为 y 的另一个名字(但要注意 ≡ 也可以意味着其他东西，比如恒等)。	cosh x := (1/2)(exp x + exp (−x)) （别问，我也看不懂）	被定义为
	≡
	:⇔		P :⇔ Q 意味着 P 被定义为逻辑运算上等价于 Q。	A XOR B :⇔ (A ∨ B) ∧ ¬(A ∧ B)
	()	优先组合	优先进行括号内的运算	(8/4)/2 = 2/2 = 1, 而 8/(4/2) = 8/2 = 4。	(好像没有)
	├	推论	x ├ y 意味着 y 推导自 x。	A → B ├ ¬B → ¬A	推论；推导
数量符号	π	圆周率	圆的周长和直径的比值		[paɪ]
	e	自然常数			[iː]
	φ	黄金分割数	把一条线段分割为两部分，使较大部分与全长的比值等于较小部分与较大的比值，则这个比值即为黄金分割。		[faɪ]
	i	虚数单位	规定 i²=-1		[ai]
	(好像找不到)	毕达哥拉斯常数	根号2	自己算去	Runtime Error
运算符号	四则运算符号	+、-、×或·、÷或/	懒……
	集合运算符号	∩	交集	设A，B是两个集合，由所有属于集合A且属于集合B的元素所组成的集合，叫做集合A与集合B的交集（intersection）。即：A∩B= {x|x∈A∧x∈B}。	交
		∪	并集	若A和B是集合，则A和B并集是有所有A的元素和所有B的元素，而没有其他元素的集合。A和B的并集通常写作 "A∪B"，读作“A并B”，用符号语言表示，即：A∪B={x|x∈A,或x∈B}	并
	对数	log	对数(logarithms)	求幂的逆运算.如果a的x次方等于N（a>0，且a≠1），那么数x叫做以a为底N的对数（logarithm），记作x=loga N。其中，a叫做对数的底数，N叫做真数。	[lɒɡ]
		lg	以10为底的对数	lg a = log10 a,计算机里面的log其实就是lg	lg……吧
		ln	以无理数e为底的对数	ln a = loge a	ln……吧
		lb	以2为底的对数,多用于计算机	lb n = log2 n	lb……吧
		lim	极限对数	某一个函数中的某一个变量，此变量在变大（或者变小）的永远变化的过程中，逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”（“永远不能够等于A，但是取等于A‘已经足够取得高精度计算结果）的过程。	limits……吧
	:	比	懒……
	||	绝对值符号
能用到的基本都在这了……

补充：快读快写

正常的输入输出是不是

cin >> a;
cout << a;

如果是要用文件读入的话

freopen("", "", );
fopen("", "");
fstream fin("");

我们在这里使用

fstream fin("");

对输入输出进行优化

---

有没有听教练说过iostream比cstdio慢？

为什么呢？

首先我们要知道他们的工作原理。

cstdio的话……我找不到代码了

他们是不断调用底层程序，而且需要有格式化字符串（就是前面你写的一大堆）来识别变量类型。相对来说会快。

但是iostream的话，他们使用的是重定义运算符。而且你有没有发现iostream有很多花里胡哨的操作？

他们所依靠的operator<<函数进行的是格式化输入，这意味着，每次你调用的时候它们都必须做大量工作。它们必须建立和销毁sentry对象（为每个operator<<调用进行建立和清除活动的特殊的iostream对象），

它们必须检查可能影响它们行为的流标志（比如skipws），它们必须进行全面的读取错误检查，而且如果它们遇到问题，它们必须检查流的异常掩码来决定是否该抛出一个异常。

如果进行格式化输入，这些都是重要的活动，但如果你需要的只是从输入流中抓取下一个字符，这样做就过度了。

（不错，复制自CSDN）

那咋整？

上面是不是说，他们必须检查很多东西，而且要不断调用IO，所以慢。

那我们就优化一下，使用缓存输入输出。到最后一次性输出，看你还能怎么慢。