[JSOI2010]部落划分
题目
聪聪研究发现，荒岛野人总是过着群居的生活，但是，并不是整个荒岛上的所有野人都属于同一个部落，野人们总是拉帮结派形成属于自己的部落，不同的部落之间则经常发生争斗。只是，这一切都成为谜团了——聪聪根本就不知道部落究竟是如何分布的。
不过好消息是，聪聪得到了一份荒岛的地图。地图上标注了 \(n\) 个野人居住的地点（可以看作是平面上的坐标）。我们知道，同一个部落的野人总是生活在附近。我们把两个部落的距离，定义为部落中距离最近的那两个居住点的距离。聪聪还获得了一个有意义的信息——这些野人总共被分为了 \(k\) 个部落！这真是个好消息。聪聪希望从这些信息里挖掘出所有部落的详细信息。他正在尝试这样一种算法：
对于任意一种部落划分的方法，都能够求出两个部落之间的距离，聪聪希望求出一种部落划分的方法，使靠得最近的两个部落尽可能远离。
例如，下面的左图表示了一个好的划分，而右图则不是。请你编程帮助聪聪解决这个难题。
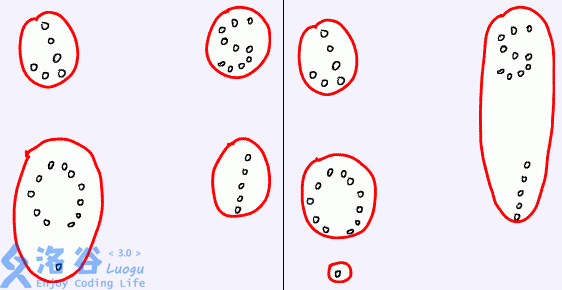
输入格式
输入文件第一行包含两个整数 n 和 k，分别代表了野人居住点的数量和部落的数量。
接下来 \(n\) 行，每行包含两个整数 \(x\)，\(y\)，描述了一个居住点的坐标。
输出格式
输出一行一个实数，为最优划分时，最近的两个部落的距离，精确到小数点后两位。
输入输出样例
输入 #1
4 2
0 0
0 1
1 1
1 0
输出 #1
1.00
输入 #2
9 3
2 2
2 3
3 2
3 3
3 5
3 6
4 6
6 2
6 3
输出 #2
2.00
说明/提示
数据规模与约定
对于 100%100% 的数据，保证 \(2 \leq k \leq n \leq 10^3，0 \leq x, y \leq 10^4\)。
传送门
题意
定义平面上两个点集之间的距离
把平面上的n个点划分成k个点集，求每个点集之间的距离最小值最大
思路
二分答案
首先看见最小值最大或者最大值最小，我们可以果断选择二分答案
界限
下界不用说，距离最小就是0
上界就是距离最远的两个点的距离，这里假设是最左下角和最右上角，那么上界就是\(1e5 \sqrt2\)
区间转移
定义中点\(mid = (l+r)/2\),这题由于要求输出两位小数，根据作者亲测用\(float\)连样例都过不了，还是专心用\(double\)好了
定义函数check(double k), 如果存在一种划分方法，使得各个部落之间的距离大于等于k，那么返回真，否则返回假
如果是真，就代表答案就是这个或者有可能更大，下界上移
如果是假，就代表这个数以及这个数上面的数都不能成为答案，上界下移
while(l + 1e-4 <= r)
{
mid = (l + r) / 2;
if(check(mid)) l = ans = mid;
else r = mid;
}
这里要特别注意，虽然是两位小数，我们还是要用到\(1e-4\)的精度，如果是\(1e-3\)或者\(5e-4\)都只能拿到\(90pts\)的好成绩。如果精度过高有可能时间上过不去。
至于check函数，后面会讲到
并查集
并查集就是路径压缩，最简单的就是查找亲戚。如果一个人和你有共同的祖先，那么你们一定是亲戚（要多少杆子才能打得着就不知道了）
亲戚
如果我们定义数组\(fa[i]\)表示\(i\)的祖先，如果\(fa[a]=fa[b]\),那么\(a\)和\(b\)就是亲戚
找最远祖先（路径压缩）
因为我要找祖先，只要我的祖先不是我（初始化每个人的祖先为自己），那么我就肯定不是我的最远祖先（废话头上就有一个人比你大了）
我们知道
while(x != fa[x]) x = fa[x];
就可以找到祖先
但是这样一次次跳不是太麻烦了吗
我们就优化一下
while(x != fa[x]) x = fa[x] = fa[fa[x]];
这样不仅一次跳了两下，而且还更新了父亲的值为爷爷，这样以后询问的时候可以直接问爷爷，不用问父亲再让父亲问爷爷了。
然而这样还不是最简单的
inline int fd(int x)
{
if(fa[x] != x) fa[x] = fd(fa[x]);
return fa[x];
}
只要我的祖先不是我，那么我就一定要问出来现在我的最远祖先是谁，我先记下来，以后有变动的时候直接问他：“你还是不是我的最远祖先”，不用去问中间一堆人。
认亲戚（合并集合）
那么我们也知道，人有悲欢离合，月有阴晴圆缺，难免我们会认亲戚
如果\(a\)属于一个家族，\(b\)属于一个家族，现在突然发现\(a\)和\(b\)有血缘关系，那么这两个家族就变成了亲戚（我也不知道为啥）
计算机世界里才不管谁占便宜，只要是亲戚，不妨让\(a\)的最远祖先认\(b\)的最远祖先为XX（此内容已被和谐化）
这样整个\(a\)家族的人找祖先的时候，问\(a\)的最远祖先：
”你还是不是我的最远祖先？“
“不是，我的最远祖先是XX了，所以你们的最远祖先也是XX”
认亲的过程很简单，一行搞定
inline void add(int a, int b)
{
fa[fd(a)] = fd(b);
}
总结
并查集就是路径压缩，集合合并。
每个点通过路径压缩存他的最远祖先，合并的时候只需要连一条边就好了。
回到题目
其实大体思路已经在“二分答案”中讲过了，现在主要来讲check函数
bool check(double m)
首先并查集初始化，每个人的最远祖先都是自己
然后开始\(O(n^2)\)的遍历……（我也不知道为啥没炸）
如果两个点在一个集合中，那么他们就是一个部落的，一定能通过某些小于m的路径相互到达。
遍历出两个点\(i, j\)， 他们的最远祖先分别是\(a, b\)
如果这两个点在一个集合中，也就是说他们是一个部落的，那么我们其实不用遍历了
否则：
如果\(Dis_{i, j} <= m\),那么就可以说明\(i\)所在的集合和\(j\)所在的集合其实是同一个部落，我们就把他们合并
到了最后我们看看还剩下多少个部落，如果部落数\(>=k\)那么返回真，否则返回假
怎么统计部落数呢？
如果我的最远祖先是我自己，那么我就是这个部落的酋长。
如果我的最远祖先不是我自己，那么我就不是这个部落的酋长。
易得一个部落只有一个酋长。
所以统计一下酋长的数量就可以了。
inline bool check(const double m)
{
register int num = 0;
for(register int i = 1 ; i <= n; i++)
{
fa[i] = i;
}
for(int i = 1; i < n; i++)
{
for(int j = i + 1; j <= n; j++)
{
const int a = fd(i), b = fd(j);
if(a == b) continue;
if(house[i] - house[j] <= m)
{
add(i, j);
}
}
}
for(int i = 1; i <= n; i++)
{
if(fa[i] == i) num ++;
}
return num >= k;
}
代码
#include <bits/stdc++.h>
using namespace std;
int n, k;
map <pair<int, int>, int> mp;
struct lce_pos
{
int x, y;
}house[10001];
double operator - (lce_pos a, lce_pos b)
{
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
int fa[10001];
inline int fd(int x)
{
if(fa[x] != x) fa[x] = fd(fa[x]);
return fa[x];
}
inline void add(int a, int b)
{
fa[fd(a)] = fd(b);
}
double ans, l, r, mid;
bool check(const double);
int main()
{
cin >> n >> k;
for(int i = 1; i <= n; i++)
{
scanf("%d%d", &house[i].x, &house[i].y);
}
l = 0;
r = 1e4 * sqrt(2) + 1;
while(l + 1e-4 <= r)
{
mid = (l + r) / 2;
if(check(mid)) l = ans = mid;
else r = mid;
}
cout << setprecision(2) << fixed << ans << endl;
return 0;
}
inline bool check(const double m)
{
register int num = 0;
for(register int i = 1 ; i <= n; i++)
{
fa[i] = i;
}
for(int i = 1; i < n; i++)
{
for(int j = i + 1; j <= n; j++)
{
const int a = fd(i), b = fd(j);
if(a == b) continue;
if(house[i] - house[j] <= m)
{
add(i, j);
}
}
}
for(int i = 1; i <= n; i++)
{
if(fa[i] == i) num ++;
}
return num >= k;
}
