结对项目-实现一个自动生成小学四则运算题目的命令行程序
| 这个作业属于哪个课程 | https://edu.cnblogs.com/campus/gdgy/CSGrade22-34 |
|---|---|
| 这个作业要求在哪里 | 结对项目 - 作业 - 计科22级34班 - 班级博客 - 博客园 (cnblogs.com) |
| 这个作业的目标 | 实现一个自动生成小学四则运算题目的命令行程序 |
| 成员 | 3122004742 李思危 3122004754 许佳钒 |
| github地址 | vvvvv19/homework3: 软工homework3 (github.com) |
一、需求
1题目：实现一个自动生成小学四则运算题目的命令行程序（也可以用图像界面，具有相似功能）
2说明：
自然数：0, 1, 2, …。
- 真分数：1/2, 1/3, 2/3, 1/4, 1’1/2, …。
- 运算符：+, −, ×, ÷。
- 括号：(, )。
- 等号：=。
- 分隔符：空格（用于四则运算符和等号前后）。
- 算术表达式：
e = n | e1 + e2 | e1 − e2 | e1 × e2 | e1 ÷ e2 | (e),
其中e, e1和e2为表达式，n为自然数或真分数。
- 四则运算题目：e = ，其中e为算术表达式。
3.需求
1.使用 -n 参数控制生成题目的个数，例如
Myapp.exe -n 10
将生成10个题目。
2.使用 -r 参数控制题目中数值（自然数、真分数和真分数分母）的范围，例如
Myapp.exe -r 10
将生成10以内（不包括10）的四则运算题目。该参数可以设置为1或其他自然数。该参数必须给定，否则程序报错并给出帮助信息。
3.生成的题目中计算过程不能产生负数，也就是说算术表达式中如果存在形如e1− e2的子表达式，那么e1≥ e2。
4.生成的题目中如果存在形如e1÷ e2的子表达式，那么*其结果应是真分数*。
5.*每道题目中出现的运算符个数不超过3个。*
6.程序一次运行生成的题目不能重复，*即任何两道题目不能通过有限次交换+和×左右的算术表达式变换为同一道题目*。例如，23 + 45 = 和45 + 23 = 是重复的题目，6 × 8 = 和8 × 6 = 也是重复的题目。*3+(2+1)和1+2+3这两个题目是重复的，由于+是左结合的，1+2+3等价于(1+2)+3，也就是3+(1+2)，也就是3+(2+1)。但是1+2+3和3+2+1是不重复的两道题，因为1+2+3等价于(1+2)+3，而3+2+1等价于(3+2)+1，它们之间不能通过有限次交换变成同一个题目。*
生成的题目存入执行程序的当前目录下的Exercises.txt文件，格式如下：
- 四则运算题目1
- 四则运算题目2
……
其中真分数在输入输出时采用如下格式，真分数五分之三表示为3/5，真分数二又八分之三表示为2’3/8。
7.在生成题目的同时，计算出所有题目的答案，并存入执行程序的当前目录下的Answers.txt文件，格式如下：
- 答案1
- 答案2
特别的，真分数的运算如下例所示：1/6 + 1/8 = 7/24。
8.程序应能支持一万道题目的生成。
9.程序支持对给定的题目文件和答案文件，判定答案中的对错并进行数量统计，输入参数如下：
Myapp.exe -e
统计结果输出到文件Grade.txt，格式如下：
Correct: 5 (1, 3, 5, 7, 9)
Wrong: 5 (2, 4, 6, 8, 10)
其中“:”后面的数字5表示对/错的题目的数量，括号内的是对/错题目的编号。为简单起见，假设输入的题目都是按照顺序编号的符合规范的题目。
二、PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时（分钟） | 实际耗时（分钟） |
|---|---|---|---|
| Planning | 计划 | 20 | 20 |
| Estimate | 估计这个任务需要多少时间 | 20 | 20 |
| Development | 开发**** | 415 | 565 |
| Analysis | 需求分析 (包括学习新技术) | 70 | 180 |
| Design Spec | 生成设计文档 | 40 | 35 |
| Design Review | 设计复审 | 15 | 15 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 20 | 15 |
| Design | 具体设计 | 60 | 60 |
| Coding | 具体编码 | 120 | 180 |
| Code Review | 代码复审 | 30 | 20 |
| Test | 测试（自我测试，修改代码，提交修改） | 60 | 60 |
| Reporting | 报告 | 80 | 75 |
| Test Report | 测试报告 | 45 | 45 |
| Size Measurement | 计算工作量 | 10 | 10 |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 25 | 20 |
| 合计 | 515 | 660 |
三.效能分析
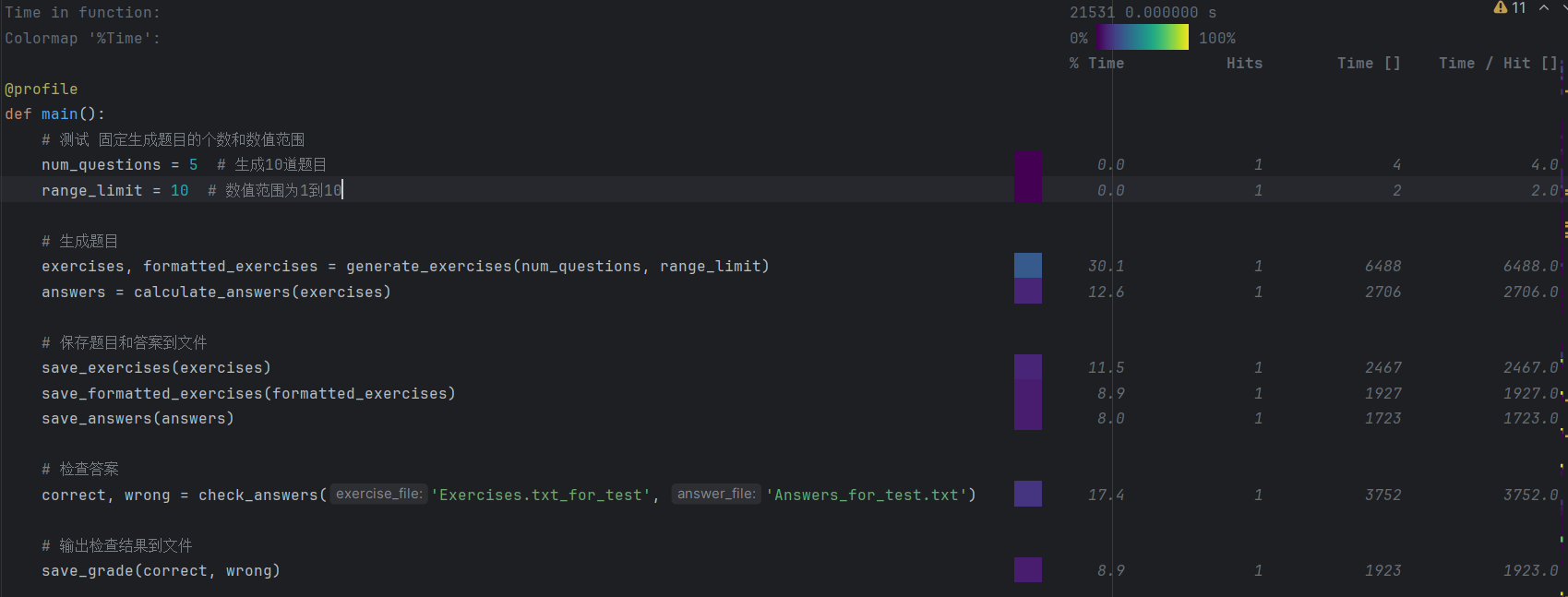
通过效能分析，能看到生成题目函数 generate_exercises占用的时间最多，有30.1%约6.5毫秒，其次是检查答案函数check_answers占比17.4约3.8毫秒，计算答案函数calculate_answers占比12.6%约2.8毫秒
四.设计实现过程
1.设计思路
程序旨在生成和检查算术题目，具体包括生成随机的整数和分数算式，并验证用户的答案。
（1）随机题目生成：
题目数量和范围：用户指定要生成的题目数量和操作数的范围。
操作数和运算符：随机选择操作数的数量（2至4个），然后随机生成每个操作数，可能是整数或分数。同时，随机选择运算符（加、减、乘、除）来组合操作数形成完整的算式。
结果计算：通过 eval() 函数计算表达式的值，并确保结果有效（不为负数且不引发除零错误）。
（2）答案格式化
使用辅助函数将分数转换为带分数形式，确保题目以易于理解的方式呈现。
（3）答案检查
读取文件：程序从指定的文件中读取题目和用户提交的答案。
逐一比较：对每道题目，计算其期望答案，并与用户提供的答案进行比较。记录正确和错误的题目索引。
（4）输出结果
返回正确和错误题目的索引，便于用户了解哪些题目答对了，哪些需要改正。
2.函数设计
（1）题目生成函数
generate_exercises(num_questions, range_limit)：它首先定义运算符和存储题目的集合。然后，它在循环中随机选择操作数的数量（2到4个），并生成每个操作数，可能是整数或分数，分数会被格式化为带分数的形式。接着，随机选择运算符并组合生成表达式。函数会计算表达式的结果，确保不为负数且无除零错误。如果有效，就将生成的表达式及其带分数形式保存。最后，函数返回普通格式和带分数格式的题目列表。
calculate_answers(exercises)：使用eval计算字符串得到正确答案，然后将答案转化成代分数
（2）格式化函数
format_mixed_number(fraction)：它将分数格式化为带分数的形式，它计算数的整数部分和分数部分，返回格式化后的字符串表示
（3）写文件函数
save_exercises(exercises)：保存题目到文件
save_formatted_exercises(formatted_exercises)：保存带分数形式的题目到文件（做题者看到的是这个）
save_answers(answers)：保存答案到文件
（4）答案检查函数
check_answers(exercise_file, answer_file)：从指定的文件中读取题目和用户提交的答案。对每道题目，计算其期望答案，并与用户提供的答案进行比较。记录正确和错误的题目索引。
save_grade(correct, wrong)：保存正确和错误的题目索引，写成文件。
五.代码分析
1.关键代码 generate_exercises(num_questions, range_limit) 题目生成
先定义运算符和存储题目的集合。然后，它在循环中随机选择操作数的数量（2到4个），并生成每个操作数，可能是整数或分数，分数会被格式化为带分数的形式。接着，随机选择运算符并组合生成表达式。函数会计算表达式的结果，确保不为负数且无除零错误。如果有效，就将生成的表达式及其带分数形式保存。最后，函数返回普通格式和带分数格式的题目列表。
def generate_exercises(num_questions, range_limit):
operators = ['+', '-', '*', '/'] # 可用的运算符
exercises = set() # 用于存储唯一题目的集合
exercise_pairs = [] # 用于保存题目及其带分数形式的元组
# 循环直到生成指定数量的题目
while len(exercises) < num_questions:
num_operands = random.randint(2, 4) # 随机选择操作数的数量（2到4个）
nums = [] # 存储生成的操作数
formatted_nums = [] # 存储格式化后的操作数（带分数形式）
# 生成操作数
for _ in range(num_operands):
if random.choice([True, False]):
# 随机生成一个整数
num = random.randint(1, range_limit)
nums.append(str(num)) # 将整数转换为字符串
formatted_nums.append(str(num)) # 原样保存整数
else:
# 随机生成分数的分子和分母
numerator = random.randint(1, range_limit - 1) # 分子
denominator = random.randint(2, range_limit) # 分母（分母不为0）
fraction = Fraction(numerator, denominator) # 创建分数对象
formatted_fraction = format_mixed_number(fraction) # 格式化为带分数
nums.append(f"{fraction}") # 将分数转换为字符串
formatted_nums.append(f"{formatted_fraction}") # 保存带分数形式
# 随机选择运算符
random_ops = random.choices(operators, k=num_operands - 1)
# 创建表达式
expr = nums[0]
formatted_expr = formatted_nums[0] # 初始化格式化表达式
for i in range(num_operands - 1):
# 根据运算符的类型选择如何组合表达式
if random_ops[i] in ['+', '-']:
expr = f"({expr} {random_ops[i]} {nums[i + 1]})" # 对加法和减法使用括号
formatted_expr = f"({formatted_expr} {random_ops[i]} {formatted_nums[i + 1]})" # 处理格式化表达式
else:
expr += f" {random_ops[i]} {nums[i + 1]}" # 对乘法和除法直接连接
formatted_expr += f" {random_ops[i]} {formatted_nums[i + 1]}"
# 去掉最外层的括号
if expr.startswith('(') and expr.endswith(')'):
expr = expr[1:-1] # 去掉普通表达式的括号
if formatted_expr.startswith('(') and formatted_expr.endswith(')'):
formatted_expr = formatted_expr[1:-1] # 去掉格式化表达式的括号
try:
result = eval(expr) # 计算结果
if result < 0: # 结果不能为负数
continue
except ZeroDivisionError:
continue # 捕获除零错误，继续下一轮
except SyntaxError:
continue
exercises.add(expr) # 将有效表达式添加到集合
exercise_pairs.append((expr, formatted_expr)) # 保存题目及其格式化形式
# 分离出题目和带分数形式
exercises, formatted_exercises = zip(*exercise_pairs) if exercise_pairs else ([], [])
return list(exercises), list(formatted_exercises) # 返回题目和格式化题目的列表
2.关键代码check_answers(exercise_file, answer_file) 检查答案
从指定的文件中读取题目和用户提交的答案。对每道题目，计算其期望答案，并与用户提供的答案进行比较。记录正确和错误的题目索引。
def check_answers(............................................................................exercise_file, answer_file):
with open(exercise_file, 'r') as ef, open(answer_file, 'r') as af:
#读取题目和答案
exercises = ef.readlines()
answers = af.readlines()
correct = [] # 存储正确答案的题目索引
wrong = [] # 存储错误答案的题目索引
# 遍历每个题目和对应的答案并组成元组生成索引
for i, (exercise, answer) in enumerate(zip(exercises, answers)):
# 计算题目的期望答案，并格式化为代分数形式
expected_answer = format_mixed_number(Fraction(eval(exercise.strip())).limit_denominator())
# 检查期望答案与用户答案是否匹配
if expected_answer.strip() == answer.strip():
correct.append(i + 1)#正确的加入正确列表
else:
wrong.append(i + 1)#错误的加入错误列表
return correct, wrong
六.测试运行
在程序中，有test_main.py对程序进行单元测试，以下是程序的部分测试用例
1.测试格式化函数
#测试格式化函数 该测试结果应为不通过
def test_format_mixed_number(self):
self.assertEqual(format_mixed_number(Fraction(5, 2)), "2'1/2")
self.assertEqual(format_mixed_number(Fraction(3, 1)), "3")
self.assertEqual(format_mixed_number(Fraction(1, 3)), "1/3")
self.assertEqual(format_mixed_number(Fraction(-3, 2)), "-1'1/2")
self.assertEqual(format_mixed_number(Fraction(0, 1)), "0")
#测试验证格式化函数在处理边界情况时的正确性
def test_format_mixed_number_edge_cases(self):
self.assertEqual(format_mixed_number(Fraction(1, 1)), "1")
self.assertEqual(format_mixed_number(Fraction(10, 3)), "3'1/3")
self.assertEqual(format_mixed_number(Fraction(-10, 3)), "-3'1/3")
通过测试边界情况，程序的健壮性得到了验证,以及结果验证，验证了计算的正确性
2.测试题目生成函数
#测试生成题目函数生成的题目数量
def test_generate_exercises(self):
exercises, formatted_exercises = generate_exercises(5, 10)
self.assertEqual(len(exercises), 5)
self.assertEqual(len(formatted_exercises), 5)
for exercise in exercises:
self.assertTrue(any(op in exercise for op in ['+', '-', '*', '/']))
#测试算数结果是否非负
def test_generate_exercises_negative(self):
exercises, _ = generate_exercises(100, 10) # 假设生成100道题目
self.assertTrue(all(eval(ex) >= 0 for ex in exercises))
#测试生成函数函数在处理较大范围时的正确性
def test_generate_exercises_with_large_range(self):
exercises, formatted_exercises = generate_exercises(5, 100)
self.assertEqual(len(exercises), 5)
self.assertTrue(all(eval(ex) <= 100 for ex in exercises))
测试确保生成的算术结果是非负的，以符合题目要求，并测试了题目生成数量，以确保题目数量准确，同时也确保函数在较大范围内生成题目时，仍能保持正确的题目数量和计算结果范围。
3.测试计算答案函数
#测试答案函数计算的答案是否正确 该测试结果应为不通过
def test_calculate_answers(self):
exercises = ["2 + 3", "(1 + 1) * 5", "5 - 3", "7 / 1"]
answers = calculate_answers(exercises)
expected_answers = ["5", "2", "2", "7"]
self.assertEqual(answers, expected_answers)
#测试计算答案函数在处理包含分数的算式时的正确性
def test_calculate_answers_with_fractions(self):
exercises = ["1/2 + 1/4", "3/4 - 1/2", "2 * 3/4", "5 / (1/5)"]
answers = calculate_answers(exercises)
expected_answers = ["3/4", "1/4", "1'1/2", "25"]
self.assertEqual(answers, expected_answers)
测试计算函数算数以及处理分数时的准确性，确保程序正确处理并返回分数和带分数和各种数的计算结果
4.测试检查答案函数
#测试检查答案函数输出是否正确 该测试结果应为不通过
def test_check_answers(self):
with open('Exercises_test.txt', 'w') as ef:
ef.write("2 + 3\n(1 + 1) * 5\n")
with open('Answers_test.txt', 'w') as af:
af.write("5\n2\n")
correct, wrong = check_answers('Exercises_test.txt', 'Answers_test.txt')
self.assertEqual(correct, [1, 2])
self.assertEqual(wrong, [])
#测试答案正确检测函数在用户答案错误时的行为
def test_check_answers_incorrect(self):
with open('Exercises_test.txt', 'w') as ef:
ef.write("2 + 3\n(1 + 1) * 5\n")
with open('Answers_test.txt', 'w') as af:
af.write("4\n3\n") # 错误答案
correct, wrong = check_answers('Exercises_test.txt', 'Answers_test.txt')
self.assertEqual(correct, [])
self.assertEqual(wrong, [1, 2])
第一个测试验证答案检查函数在不同情况下的输出是否符合预期，第二个测试通过写入错误的答案，验证系统是否能够识别所有提供的答案都是错误的，通过这两个测试，可以全面验证答案检查函数在处理正确和错误答案时的准确性和稳定性。
5.测试总结
这些测试用例充分验证了程序的各个功能，确保其正确性，测试覆盖了所有主要功能，包括格式化分数、生成题目、计算答案、检查答案和保存成绩。每个功能都有相应的测试，确保在不同情况下都能正常工作。测试用例还包括故意错误的输入，以确保程序能够正确识别错误并返回预期结果。
七.项目小结
这个项目是结对的合作项目，我们搭档起来进行分工，在github上进行代码方面的协同合作，我们在代码的注释和规范上下了很多功夫，不然容易看不懂；同时，一个人写完一个部分代码的时候，会跑通了会上传到github上，两个人一起检查代码。在编写代码的过程中也遇到了一些bug，比如输出的问题和答案它们之间的顺序对不上，在经过不断的熬夜后也是圆满解决。
经过这个项目，我们学习到了多人合作之间交流的重要性，也知道了代码的可读性的重要性，比如函数、文件的命名需要谨慎，注释也要比较细致才行。
