27 图像卷积

27 图像卷积操作

opencv知识点：

  • 均值卷积 - blur
  • 边缘处理方式 - BorderTypes

本课所解决的问题

  • 如何理解卷积？
  • 如何理解图像卷积？
  • 如何实现对图像的均值卷积？

1.图像卷积 - 上篇

引用文章：（非常感谢这两篇博客，受益匪浅）

卷积与图像卷积

卷积

首先我们先说一下卷积

卷积一词最开始出现在信号与线性系统中，其物理意义是描述当信号激励一个线性时不变系统后发生的变化。

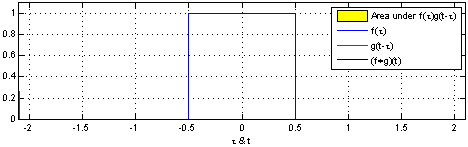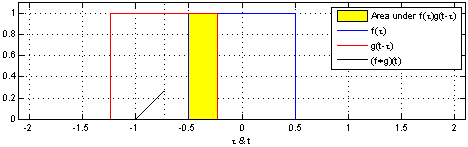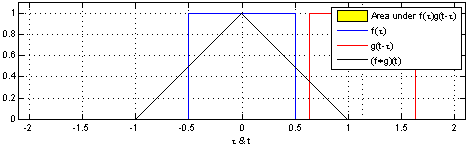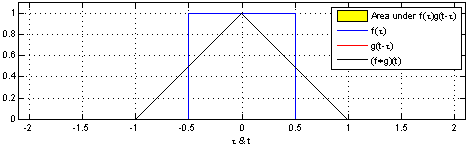
在这里插入图片描述

（1）连续时间信号的卷积：
对连续时间信号而言，卷积是一种特殊的积分运算。
它的过程就是一个函数固定不动，另一个函数先以y轴为对称轴反转，然后不断执行相乘，积分，滑动。

d3fc912719674673ac21620ef6620290

（2.）连续时间信号离散化后的卷积：
其中x(n)和h(n)是参与运算的离散时间信号。
在这个定义中，卷积的过程尤为清晰：
在坐标轴上让x(n)保持不动，先把h(n)反转，然后不断执行二者重合部分相乘求和然后让h(n)滑动的过程。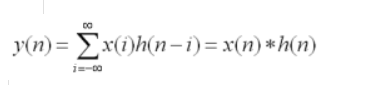

在这里插入图片描述

离散时间信号可以看作是一串序列，它是一维的。

图像卷积

如果我们把一维序列扩充为二维序列，那会怎样？那就变成了二维卷积
我们知道图像的本质就是灰度值的二维序列，扩充后的二维卷积自然就可以应用在图像上

在计算机视觉领域中，数字图像是一个二维的离散信号。
对数字图像做卷积操作，

  • 其实就是利用卷积核（卷积模板）在图像上滑动，将图像点上的像素灰度值与对应的卷积核上的数值相乘，
  • 然后将所有相乘后的值相加作为卷积核中间像素对应的图像上像素的灰度值，并最终滑动完所有图像的过程。

现在我们举几个例子

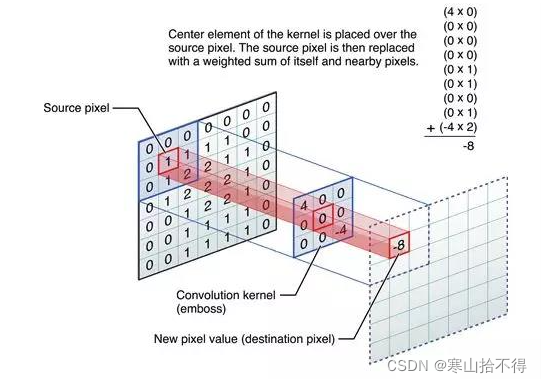
  • 图1是一个直观求卷积的示意图，从左到右看，原像素经过卷积由1变成-8。
在这里插入图片描述
  • 图2是另一张图像与另一个卷积核，并得到了不处理边缘的卷积结果

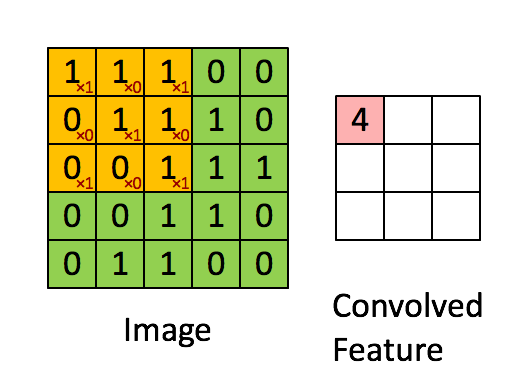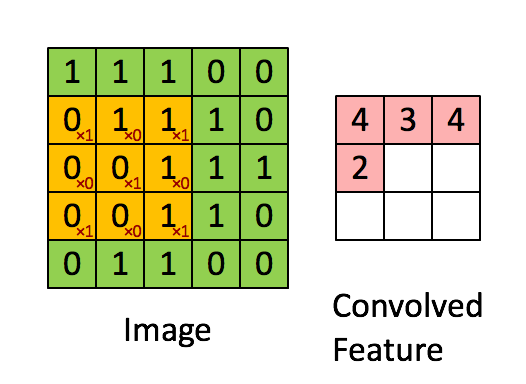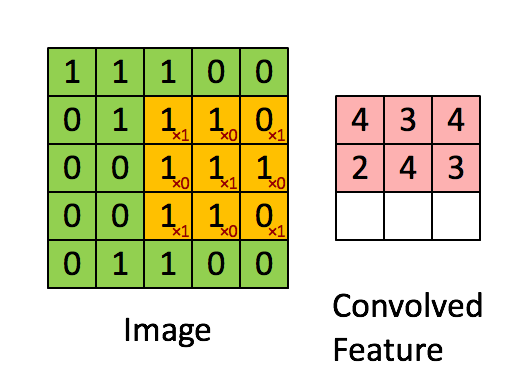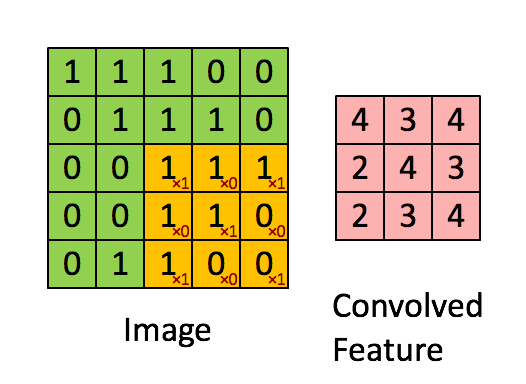
在这里插入图片描述

图像卷积的卷积核

图像卷积的概念，我们有了一个简单了解，那我们现在说一下什么是卷积核

  • 卷积核就是一种求和的规则，是一种映射的规则。
    由卷积核规则的不同衍生出了不同的卷积方式，滤波方式，不同的梯度运算方式等。

图像卷积的用途

在图像处理中，我们不会为了卷积而去卷积
因为按照卷积的定义，它只是与卷积核相乘求和的结果。
从上文的描述可以看到，单单卷积确实没什么用，因为图像卷积的用武之处不在于此。

那图像卷积的用武之地在哪？

图像卷积常常用于图像滤波（平滑化），图像梯度，开运算，闭运算，黑帽运算，顶帽运算等形态处理，以及基于梯度运算的边缘提取中。

常用图像卷积

  • 均值卷积（均值滤波/均值模糊）的卷积核如下图
    它也是按照卷积运算的过程相乘求和再滑动，只不过它的核里每个值都是1，在求和之后还除以核的大小来取平均。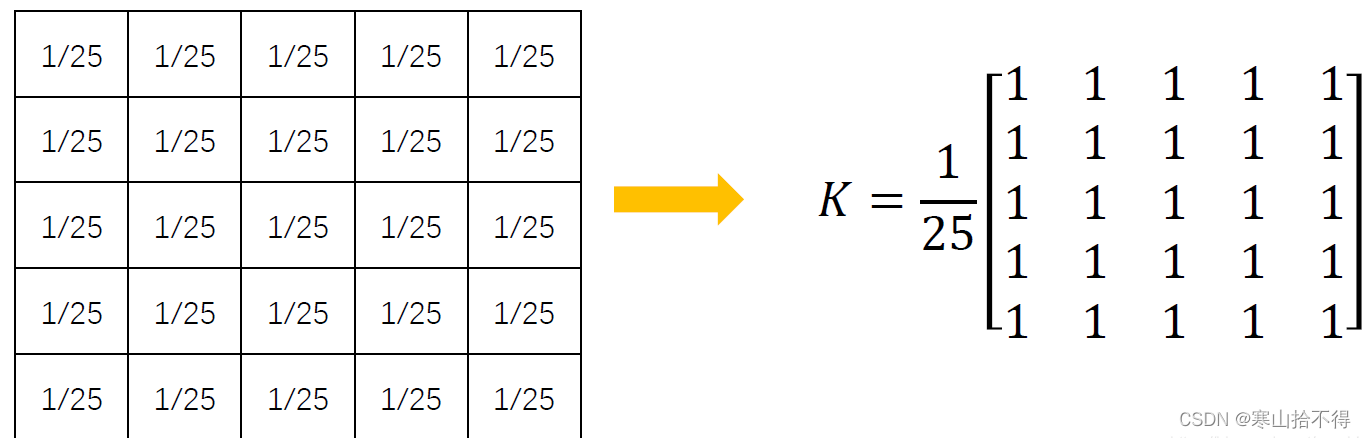

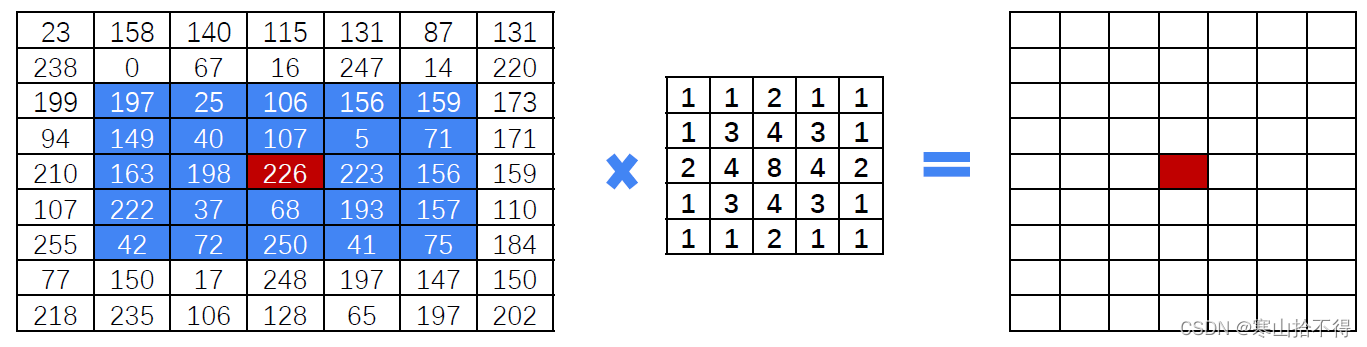
    在这里插入图片描述

  • 高斯卷积（高斯滤波/高斯模糊）的卷积核如下图
    它的核是离中心越近值越大，也就是不同位置的权重不同。
    在相乘求和之后会除以核内数值的求和值以保证灰度值不会超出范围

在这里插入图片描述

滤波/模糊

为什么上面例子的卷积也叫滤波/模糊呢？

首先说一下为什么叫滤波

滤波的本质就是卷积，不同的是要按照一定的特殊规则去卷积。
同时滤波使用的卷积核不是随意的，而是有既定的规矩的，比如：

  • 卷积核应取3x3，5x5这样的具有中心的奇数核
  • 核内数值的分布，要视不同的滤波方式而定。 如上文写到的均值滤波，它的卷积核全部都是1除以核大小。

卷积的一种应用形式就是滤波，当然不同的卷积核有不同的卷积效果，所以卷积还有诸如梯度运算等其他的应用形式，差别就在于卷积核的不同

那滤波什么作用呢？

在数字信号处理中接触的滤波，如高通滤波，是为了滤除高频信号（变化很快的信号）
而在图像滤波中也是如此，不过是过滤图像的高频成分

还是拿均值滤波来说
原图像与均值滤波卷积核卷积，结果就是原图像的像素值乘以卷积核对应位置的值相加，
对于5x5大小的核来说核内的值都是1/25，那这样看很显然，卷积的结果就是把原图像像素值相加取平均值，
这样一来像素与像素之间的差异性就变小了。
滤波后像素与像素之间的差异性减小了，这不就意味着滤除了高频成分吗？

最后说一下为什么也叫模糊

滤波后的结果就是，像素与像素之间的差异性就变小了。
图像中分明的线条和边界就是像素值迥然的差异所导致的，差异性减小导致边界就模糊了。
所以我们称其为模糊。

上篇 - 总结

总结起来就是：

  • 图像卷积靠卷积核完成
  • 卷积核规定了运算的规则
  • 滤波/模糊是卷积运算所带来的效果

不同的卷积核所得到的卷积效果不同，故衍生出了不同种类的滤波/模糊，形态运算，梯度运算等概念。

由此可见：卷积是图像处理的基础，许许多多处理方式都是离不开卷积的

2.图像卷积 - 下篇

接下来，我们看一下视频课程中的图，就很容易理解了

它采用的是

  • 均值卷积方式
  • 卷积核3x3
  • 不处理边缘
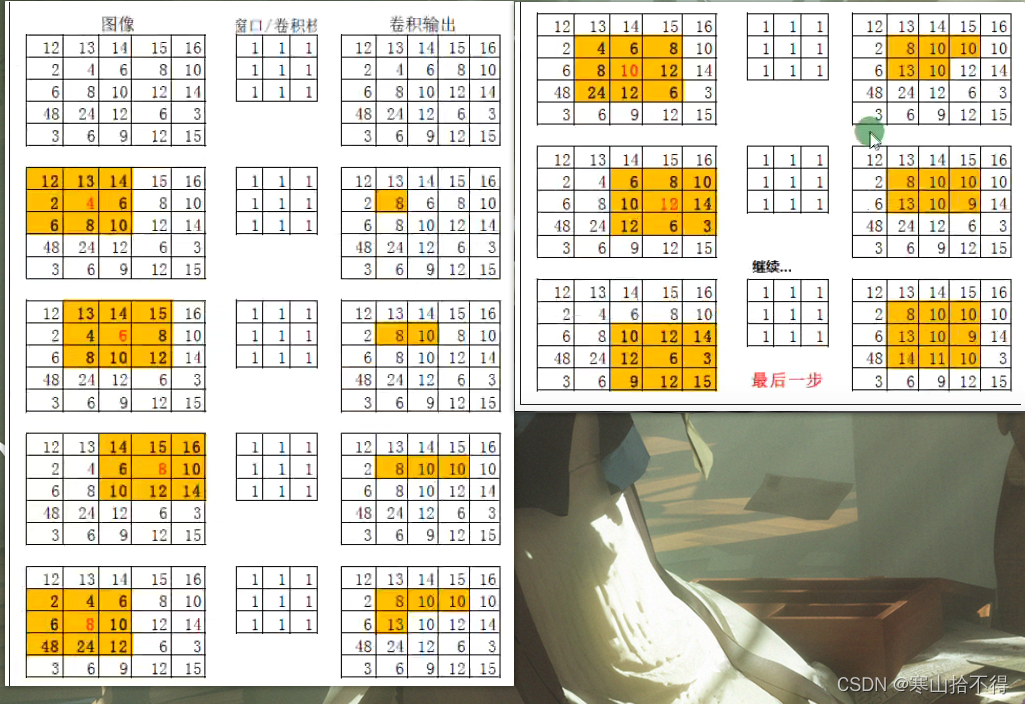
0de979fed7af43b8855d0e25c710433a

边缘处理

上面的图片演示了图像的卷积操作，但是直观的看出，卷积后的图片和卷积前的图片尺寸不一致。

对于这个问题，有两种处理策略：

  • 一是把它扔掉不管它（比如上图）

  • 二是把它周围填充起来进行处理（多数的深度学习）

深度学习有两种方式，就分别对应了上面的两种方式

  • 看重中心的——valid padding
  • 填充的——same padding

这里补充一下，卷积方式是卷积方式的，边缘处理策略是边缘处理策略的，
只要策略得当，均值卷积也能处理边缘的。

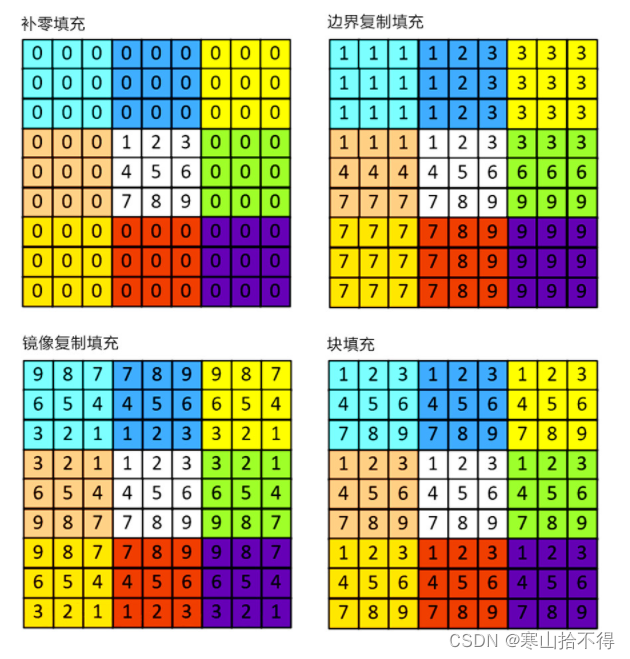
说了这么多，那怎么进行边缘填充？

提示：

  • 这里只介绍图示概念，具体实现操作在后续课程中
  • 更多的边缘处理方法，查阅官方文档可知

通常有四种方法：

在这里插入图片描述

不同卷积核的意义

最后，我们来介绍一下，不同卷积核下的图像卷积意义

图像处理中，平滑、模糊、去燥、锐化、边缘提取等等工作，其实都可以通过卷积操作来完成。
下面几个典型的卷积核效果如下：

836abb6930414023a4cd47092e4794fd 3cfb2582592b4246aaff0957d8c0dd39

从以上示例可以看出，不同的卷积核作用于图像，可以更清晰的获得图像的某种特征，如轮廓、颜色等。

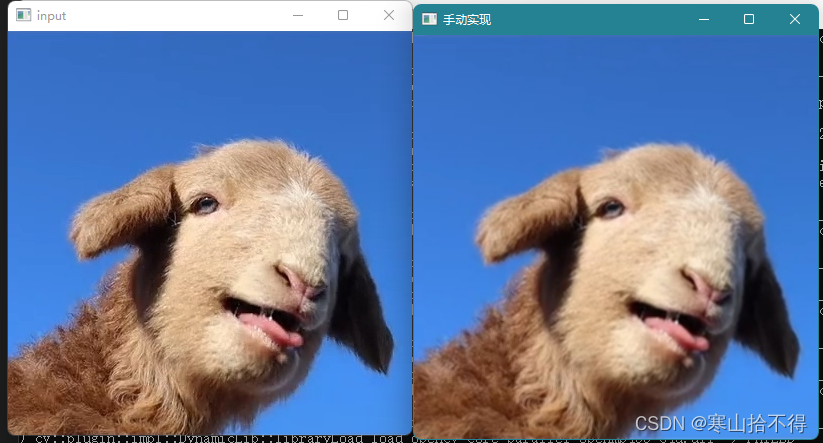
3.图像均值卷积的演示

手动实现

理解了图像卷积的概念之后，现在我们来手动实现图像的均值卷积

	int h = src.rows;
	int w = src.cols;
	Mat result = src.clone();
	
	//最外面一边我们选择不处理，忽略掉
	for (int row = 1; row < h - 1; row++) {
		for (int col = 1; col < w - 1; col++) {
			// 3x3卷积核
			int sb = src.at<Vec3b>(row, col)[0] + src.at<Vec3b>(row - 1, col - 1)[0] + src.at<Vec3b>(row - 1, col)[0] +
				src.at<Vec3b>(row - 1, col + 1)[0] + src.at<Vec3b>(row, col - 1)[0] + src.at<Vec3b>(row, col + 1)[0] +
				src.at<Vec3b>(row + 1, col - 1)[0] + src.at<Vec3b>(row + 1, col)[0] + src.at<Vec3b>(row + 1, col + 1)[0];

			int sg = src.at<Vec3b>(row, col)[1] + src.at<Vec3b>(row - 1, col - 1)[1] + src.at<Vec3b>(row - 1, col)[1] +
				src.at<Vec3b>(row - 1, col + 1)[1] + src.at<Vec3b>(row, col - 1)[1] + src.at<Vec3b>(row, col + 1)[1] +
				src.at<Vec3b>(row + 1, col - 1)[1] + src.at<Vec3b>(row + 1, col)[1] + src.at<Vec3b>(row + 1, col + 1)[1];

			int sr = src.at<Vec3b>(row, col)[2] + src.at<Vec3b>(row - 1, col - 1)[2] + src.at<Vec3b>(row - 1, col)[2] +
				src.at<Vec3b>(row - 1, col + 1)[2] + src.at<Vec3b>(row, col - 1)[2] + src.at<Vec3b>(row, col + 1)[2] +
				src.at<Vec3b>(row + 1, col - 1)[2] + src.at<Vec3b>(row + 1, col)[2] + src.at<Vec3b>(row + 1, col + 1)[2];
			result.at<Vec3b>(row, col)[0] = sb / 9;
			result.at<Vec3b>(row, col)[1] = sg / 9;
			result.at<Vec3b>(row, col)[2] = sr / 9;
		}
	}
	imshow("conv-demo", result);
1ca0bb0cb2c24d52a3d69567acb8a666

API实现

在opencv中，如果我们想实现图像的均值卷积（均值模糊/均值滤波），我们要用到这样一个API

  • blur

具体介绍如下

blur
	使用归一化框滤镜模糊图像
		共5个参数
			第1个参数 输入
			第2个参数 输出
			第3个参数 卷积核size（卷积核越大，图像模糊程度越高）
			第4个参数 锚点
					（默认值Point(-1,-1)表示锚点位于卷积后的内核中心，卷积后的值在这里更新）
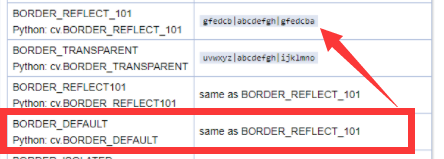
			第5个参数 图像边缘处理方式
					（默认参数 BORDER_DEFAULT 边缘有很多处理方式，查阅官方文档可知）
de1ecfdd1151463d989003ddd2762b9e 
//函数定义
void blur_demo(Mat& image);

//函数实现
void  QuickDemo::blur_demo(Mat& image) {

	imshow("原图",image);

	Mat dst;
	
	//二维卷积
	blur(image, dst, Size(3, 3));
	//blur(image, dst, Size(13, 13));

	//一维卷积
	blur(image, dst, Size(13, 1));//行卷积
	blur(image, dst, Size(1, 13));//列卷积


	imshow("图像模糊",dst);

}

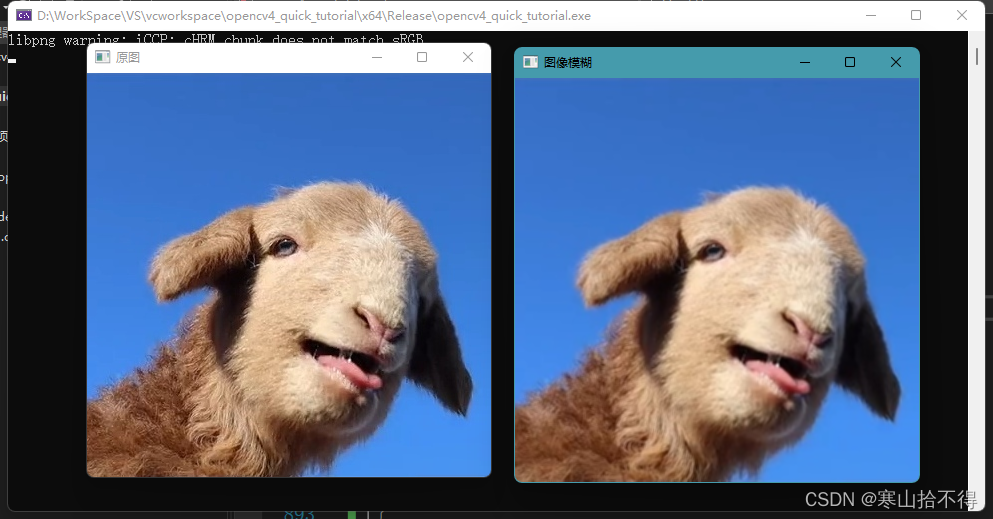
二维卷积

3 * 3
对比上面的手动实现，我们发现效果基本一样

50e26e7b469f4eba869522f9076df6ce

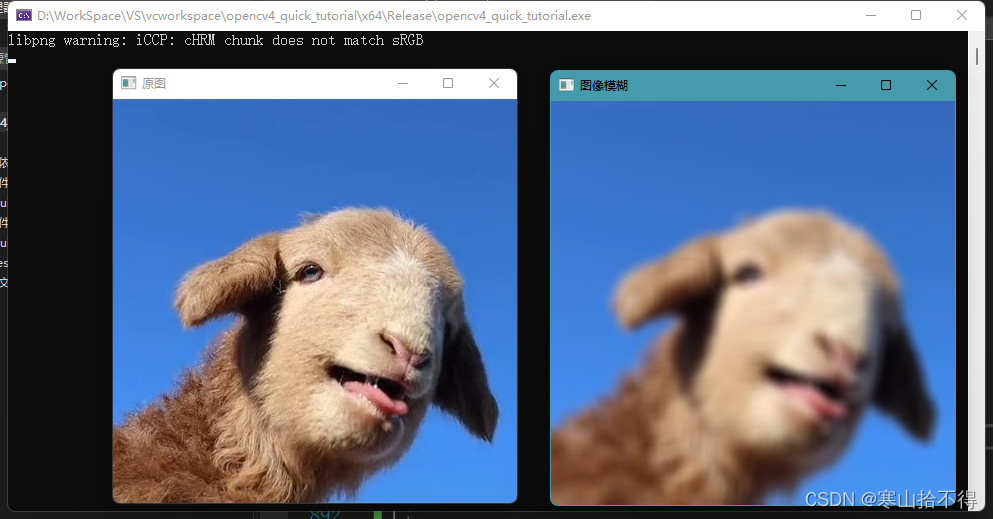
13 * 13

4fe57780e2cb4d2480c1012d9efaa14d

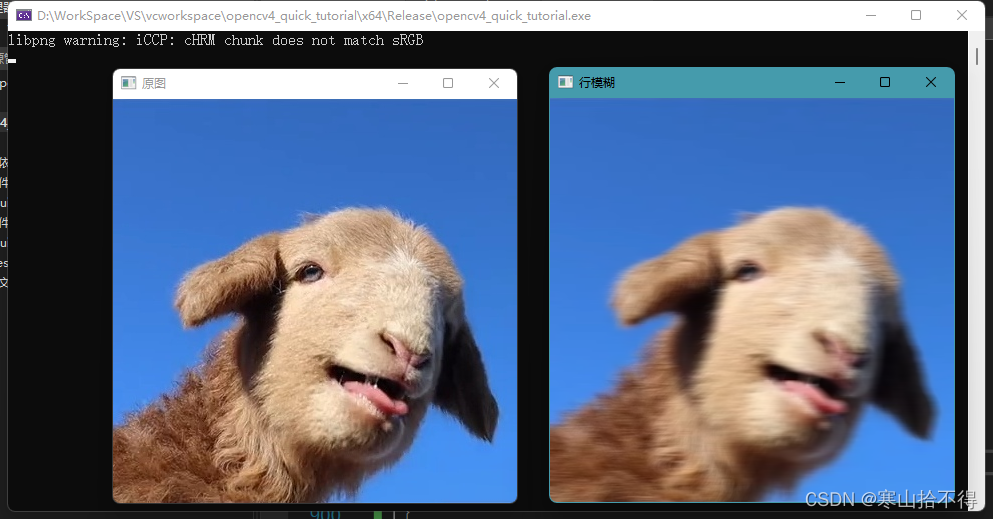
一维卷积

blur也可以实现一维的卷积

13 * 1

fcf6c9c192514111ac1c340b48fb489a

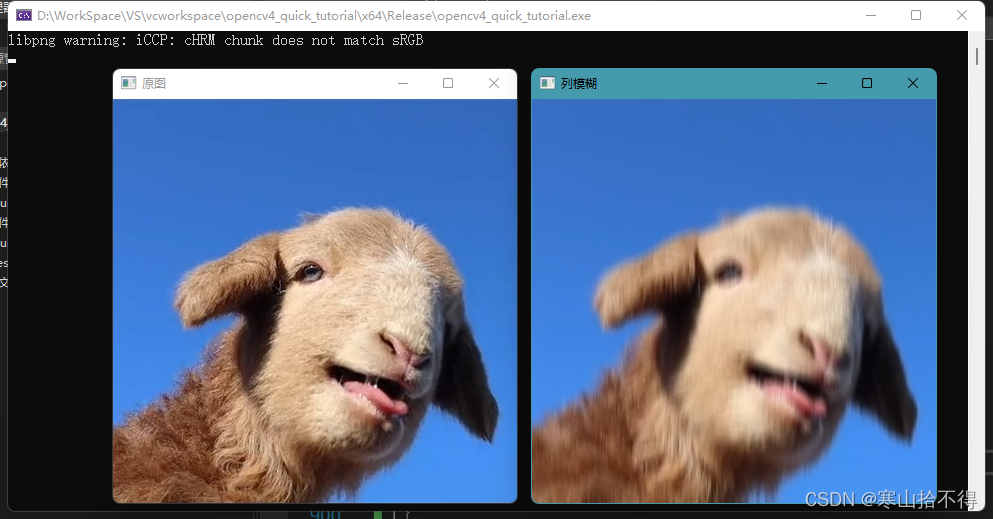
1 * 13

f067592dda534d2782b78953f96ce88f

本课所用API查阅

blur

BorderTypes

posted @ 2023-01-15 11:28  L707  阅读(281)  评论(0)  编辑  收藏  举报