笛卡尔树上计数dp
SP3734 PERIODNI - Periodni
题目传送门
前置芝士:
笛卡尔树,树上dp
笛卡尔树:
模板
笛卡尔树是一种比较小众的数据结构吧,他存放的是一个二元组 \((val , pos)\),对于 \(val\) 他满足堆得性质 ,而对于 \(pos\) 则满足 \(BST\) 的性质。那么他的性质就极好了。他的中序遍历即为原序列的顺序,若满足小根堆,则以 \(x\) 为根的子树中满足 \(val_x\)是子树中所有值最小的。
那么如何来建树呢,由于 \(pos\) 序列是单增的,那么我们考虑枚举 \(pos\),假设我们现在已经将 \(1\) ~ \(i- 1\) 的笛卡尔树已经建好了,那么我们就考虑通过添加 \(i\) 号节点并调整树的结构来构建 \(1\) ~ \(i\) 的笛卡尔树。
题目分析:
我们观察题目中的图
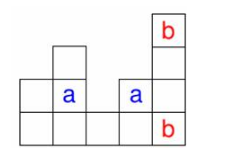
若他的高度具有单调性的话,纳闷我们就很好处理了,但是他不单调啊。
我们考虑将图按高度分一下层,然后我们发现会形成一些“山顶”,那么我们试着将图做出来。
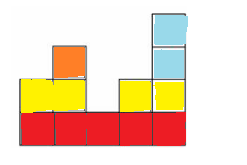
就变成了这个样子,我们发现从下到上,每一层的每一块所包含的列是发生变化的,所以我们就可以建一棵树出来了。
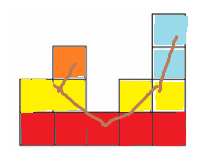
我们发现越靠下的高度越小,那么这不就是一棵笛卡尔树??!
然后我们考虑在这棵树上进行 \(dp\)。
我们令 \(f_{x,k}\) 是以 \(x\) 为根的子树中选了 \(k\) 列的方案数。我们来考虑如何进行转移,我们先不考虑他自己可以有多少种方案,只考虑子树中的方案,那么 \(f_{x,k} = \Sigma f_{i,j} * f_{x,k - j}\)。
我们将子树的所有情况合并之后,再来考虑它本身所有的情况,我们在对他所有的孩子求解完成之后,我们就知道了它本身包含多少列。那么我们就是对 \(n * m\) 的矩形进行求解,那么我们就是在 \(n\) 行中选 \(k\) 个和 \(m\)列中选 \(k\)个的方案数,又因为是排列数,所以我们还要乘上一个 \(k!\)。所以我们还需要 \(f_{x,k} = \Sigma_{j=1}^{size_x} f_{x , i - j} * C_{high}^j * C_{lie}^j * j!\)
代码:
注意本题要卡常!!
view code
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n , k;
const int M = 1e7 + 7;
int c[2][M] , a[M] , s[M];
inline int read() {
int x = 0, flag = 1;
char ch = getchar();
for( ; ch > '9' || ch < '0' ; ch = getchar()) if(ch == '-') flag = -1;
for( ; ch >= '0' && ch <= '9' ; ch = getchar()) x = (x << 3) + (x << 1) + ch - '0';
return x * flag;
}
signed main () {
ios::sync_with_stdio(0),cin.tie(0);
n = read();
int j;
int top = 0;
for(int i = 1; i <= n ;++ i) {
a[i] = read();
j = top;
while(j && a[s[j]] > a[i]) j --;
if(j) c[1][s[j]] = i;
if(j < top) c[0][i] = s[j + 1];
top = j; s[++ top] = i;
}
int L = 0 , R = 0;
for(int i = 1; i <= n; ++ i) {
L ^= i * (c[0][i] + 1);
R ^= i * (c[1][i] + 1);
}
cout << L << ' ' << R;;
}




