树状数组

树状数组

简单记录一下模板和用法，不做深入证明探究！

为什么不直接用前缀和

对于普通的前缀和来说，若出现了单点修改，则需要重新生成一个前缀和数组。若单点修改次数过多，显然会产生恐怖的代价。

能解决的问题：

• 区间查询前缀和
• 单点修改（某个值+一个数）

是一个在 logN复杂度就能完成以上操作的数据结构。严格来说，能解决的问题是线段树的子集。

树状数组能够解决的问题，线段树一定可以解决！但是树状数组代码简单好写，相比臃肿庞大的线段树，能用树状数组优雅的解决问题，想必也是让人神往的吧！

看个图例：

 

 

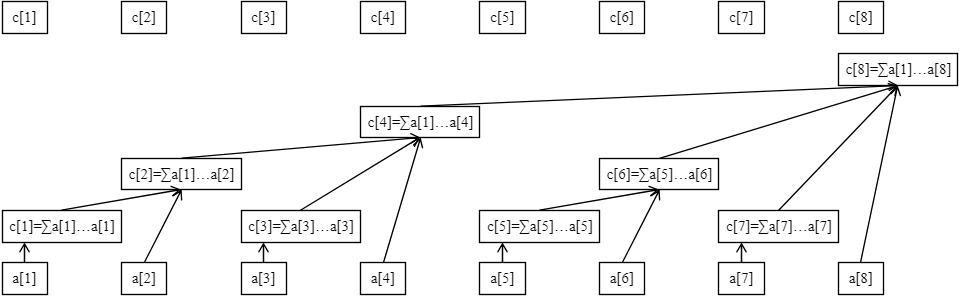
不难看出，树状数组是分层（高度）的。对于下标i在多少层，只需要将其转换成二进制，并看一下它后面有几个0就好了，若有k个0，则在2^k层

例如： （4）10 = （100）2 ，其二进制下有两个零，所以在2^2 = 4 层。

三个函数：

lowbit()

这个函数主要用来求一个数的二进制下尾数有k个0，并返回2^k。

int lowbit(int x){
    return x& -x;
}

add()

void add(int x,int v){
    //在 x 位置 加上 v
    for(int i=x;i<=n;i+=lowbit(i)) tr[i]+= v; 
}

如果不是添加，而是想替换呢？

只需要将参数V  改成 v-x即可！

query()

int query(int x){
    int res = 0;
    for(int i=x;i>0;i-=lowbit(i)) res+=tr[i];
    return res;
}

对于区间[x,y]的前缀和，我们只需要 query(y)-query(x-1) 即可！（这里用到了差分的思想）

 

初始化：

将tr数组开在全局变量，即初始化为0。对于每个输入的数，只需要调用add函数即可。

 

板子题：

这里有一个板子

 

 代码如下：

#include<iostream>
#include<cstdio>
using namespace std;
const int N = 100010;
int n,m;

int a[N],tr[N];
int lowbit(int x){
    return x& -x;
}
void add(int x,int v){
    //在 x 位置 加上 v
    for(int i=x;i<=n;i+=lowbit(i)) tr[i]+= v; 
}
int query(int x){
    int res = 0;
    for(int i=x;i>0;i-=lowbit(i)) res+=tr[i];
    return res;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    for(int i=1;i<=n;i++) add(i,a[i]);
    
    while( m --){
        int k,x,y;
        scanf("%d%d%d",&k,&x,&y);
        if(k==0){
            printf("%d\n",query(y)-query(x-1));
        }
        else{
            add(x,y);
        }
    } 
    
}