基本算法——归并排序
理论概念
定义
归并排序是基于分治法的排序方法,其时间复杂度为O(nlogn)
原理
没什么比一张Gif图片来解释排序算法更清爽了。
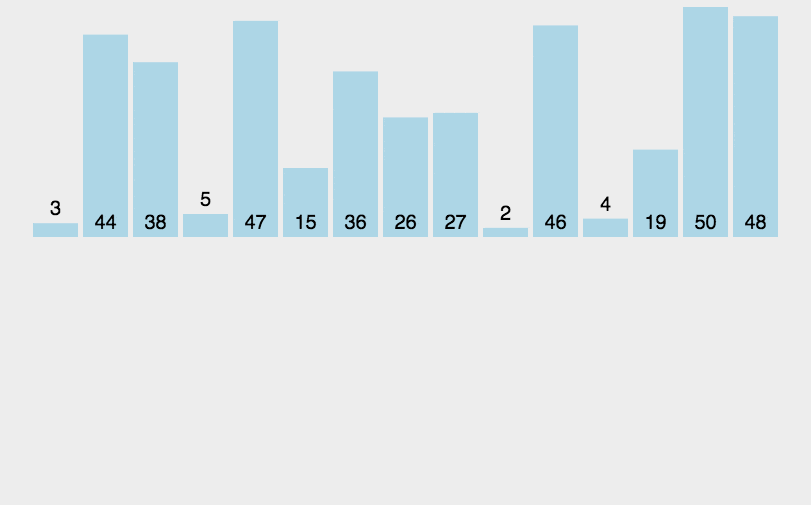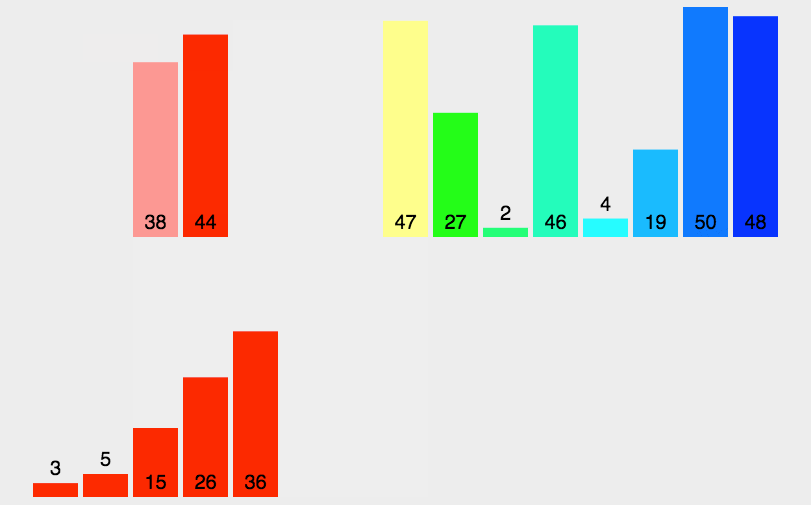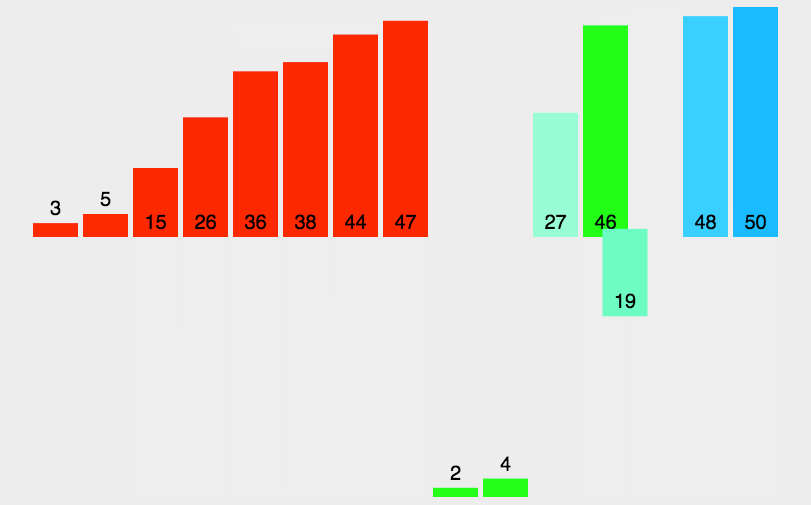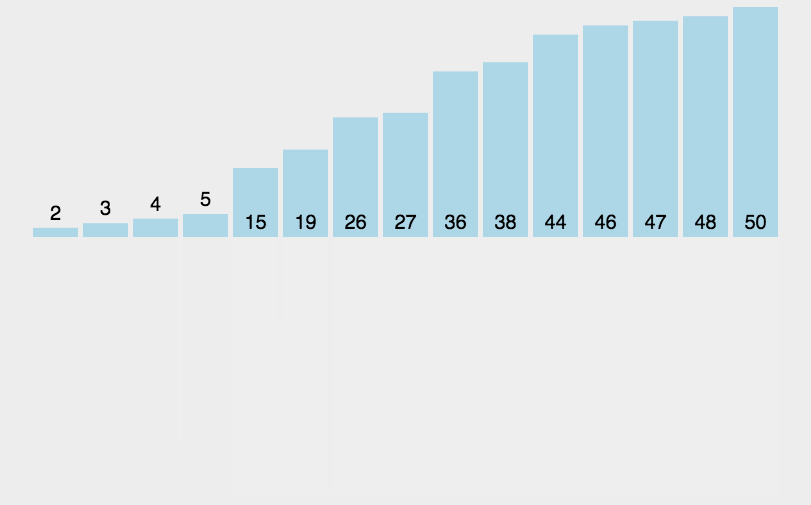
所以我就从Python的教程网站上扒了一张233
可以看到,归并排序,顾名思义。归,并。
核心代码
由于形式纷杂不好统一,这里仅列举一种展现方法。但其精髓仍是归与并的分治思想。
void merge(int l,int r) { if(l>=r) return; int mid=(l+r)/2; merge(l,mid); merge(mid+1,r); int i=l,j=mid+1,k=l-1;//此时的i是第一个数组的左端点,j是第二数组的左端点 while(i<=mid&&j<=r) { k++; if(f[i]>f[j]) { //拿两个的首项做对比,小的直接排入。 f1[k]=f[j]; ans+=mid-i+1; ans%=mod; j++; } else { f1[k]=f[i]; i++; } } while(i<=mid){k++;f1[k]=f[i];i++;}//处理剩余 while(j<=r){k++;f1[k]=f[j];j++;} for(int i=l;i<=r;i++) {//这里,归。 f[i]=f1[i]; } }
题目中的Show Time
逆序对
归并排序常被应用于关于逆序对的问题中。什么是逆序对问题?
对于一个序列a,若i<j且有A[i]>A[j],则称A[i]、A[j]构成逆序对
归并排序每次把序列二分,递归对左右俩半排序,然后合并两个有序序列。在对左右两半排序时,可以把左右两半各自内部的逆序对数作为子问题计算。故只需考虑“左边一半里一个较大的数”与“右边一半里一个较小的数”构成逆序对的情形。求出这种情形的个数。
在合并时,比较A[i]与A[j]的大小。如若A[j]小,那么A[i]~A[mid]都大于A[j]。他们都会与A[j]构成逆序对。可以顺便统计到答案中去。
代码实现如下:
void merge(int l,int mid,int r){ //合并a[l~mid]与a[mid+1~r] //a是待排序数组,b是临时数组,cnt是逆序对的个数 int i=l,j=mid+1; for(int k=l;k<=r;k++){ if(j>r||i<=mid&&a[i]<=a[j]){ b[k]=a[i++]; } else{ b[k]=a[j++]; cnt+=mid-i+1; } } for(int k=l;k<=r;k++){ a[k]=b[k]; } }
火柴排队 Noip2013提高组Day1T2

难就难在,这题怎么想到是个逆序对。(可他就是个逆序对…)
思考一下,首先必然有一种对应关系。而怎么能让这个最小距离最小呢?其实,排个序,然后大对大,小对小就能保证这个差值的绝对值之和一定是最小了。(那个所谓的平方,不如直接求abs,否则有点计算冗余)。
前面的具体思路我会在7.14校模拟里的一篇博文放出来。在这里咱们具体讨论一下关于他是个逆序对的问题。
我们得到一个映射关系之后,发现是乱序。只要我们将其复原到从小到大的顺序,那么就等于从末状态反向抵达初状态。那么这个交换步骤发生于哪里呢?理所当然,交换步骤是发生在逆序对解决归并排序的“归”之中的。
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N=100005,mod=99999997; int n; struct node{ ll x; int id; }a[N],b[N]; int c[N],d[N],f[N],f1[N]; ll ans=0; ll read(){ ll sum=0,f=1; char ch=getchar(); while(ch>'9'||ch<'0'){ if(ch=='-')f=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ sum=(sum<<3)+(sum<<1)+ch-'0'; ch=getchar(); } return sum*f; } int comp(node a,node b) { return a.x<b.x; } void merge(int l,int r) { if(l>=r) return; int mid=(l+r)/2; merge(l,mid); merge(mid+1,r); int i=l,j=mid+1,k=l-1; while(i<=mid&&j<=r) { k++; if(f[i]>f[j]) { f1[k]=f[j]; ans+=mid-i+1; ans%=mod; j++; } else { f1[k]=f[i]; i++; } } while(i<=mid){k++;f1[k]=f[i];i++;} while(j<=r){k++;f1[k]=f[j];j++;} for(int i=l;i<=r;i++) { f[i]=f1[i]; } } int main(){ // freopen("match.in","r",stdin); // freopen("match.out","w",stdout); n=read(); for(int i=1;i<=n;i++) { a[i].x=read(); a[i].id=i;} for(int i=1;i<=n;i++) { b[i].x=read(); b[i].id=i;} sort(a+1,a+n+1,comp); sort(b+1,b+n+1,comp); for(int i=1;i<=n;i++) { c[a[i].id]=i;//c数组保存的是:在i位置保存的是在a数组的第几个位置 d[i]=b[i].id; } for(int i=1;i<=n;i++){ f[i]=d[c[i]];//f中存的就是b的ID与A的映射 } merge(1,n); cout<<ans; return 0; }
能想到逆序对,说实话挺绕的。不适合作为入门级样题来做。

