最小生成树(II)与Kruskal算法

为防止网页加载过慢，故分两章。上接https://www.cnblogs.com/Uninstalllingyi/p/10479470.html

Kruskal算法——将森林合并成树

玩过瘟疫公司吗…？这一小片感染…那一小片感染…最后全部感染。诶嘿，游戏胜利。

时间复杂度

O（E*logE），E代表边数。适用于根据图生成最小生成树。

算法思想

首先要掌握两个知识点。首先是边集，然后是并查集。

把无向图中互相连通的一些点称为处于一个连通块中。（如果理解不了…其实可以理解为…相互连通的点是一个版块…或者说染成同一颜色之类的…）

图中有三个连通块。1,2处于同一个连通块中,4,5,6也处于同一个连通块中,孤立点3也称为一个连通块。然后我们利用并查集的思路，把每一个连通块看做一个集合。Kruskal首先要把所有的边按从小到大顺序排序（一般用sort，但是听闻有些变态题需要你用点更快的排序算法。）按顺序枚举边。如果两个边连接着不同的集合，那么就把他并为一个集合。如果属于同一个集合，那就跳过。所以一定是选取了n-1条边（n个点）

那么又到了最痛苦手工模拟环节。

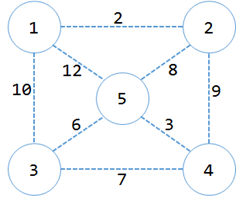
这图里，五个点。都是单独的集合好吧。开始的时候生成树里还没有边。MST就归零。

5个集合{{1},{2},{3},{4},{5}}

然后这个算法每次都选择最小的边。而且这条边的两个顶点都分属于不同的集合。然后把这个边加入最小生成树，并且合并集合。那显而易见，第一次我们选<1,2>这个边。

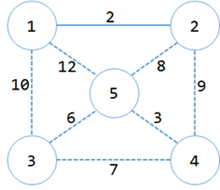
（这个图是在用实线表示）

于是得到4个集合:{{1,2},{3},{4},{5}}，生成树中有1条边{<1,2>}，MST+=2=2;

第二次我们选<4,5>

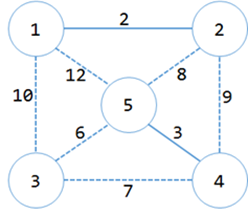
于是得到3个集合:{{1,2},{3},{4,5}}，生成树中有2条边:{<1,2>,<4,5>}，MST+=3=5;

第三次选<3,5>

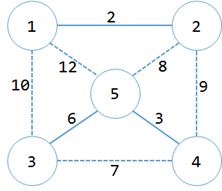
于是得到2个集合:{{1,2},{3,4,5}}，生成树中有3条边:{<1,2>,<4,5>,<3,5>}，MST+=6=11;

第四次选…你以为我会选<3,4>吗？才！不！会！因为这个边连接的3,4都属于同一个集合，所以我们这次选<2,5>

于是得到1个集合:{{1,2,3,4,5}}，生成树中有4条边:{<1,2>,<4,5>,<3,5>,<2,5>}，MST+=8=19;

经过累死累活的手算，我们发觉选边的条件是这样的：

⑴这条边的两个顶点必须分属于不同的集合
⑵在满足⑴的情况下,这条边的权值最小
⑶一张n个点的图,总共选择n-1次边

然后仔细一想…woc还是贪心的思路。

算法描述

【算法描述】
⑴定义边集数组:
struct edge{
    int x,y,v;
    bool operator<(const edge &eg)const{return v<eg.v;}
}edges[100*100];
⑵编写find函数
int find(int x){
    if(up[x]!=x) up[x]=find(up[x]);
    return up[x];
}
⑶编写join函数
bool join(int x,int y){
    if(find(x)!=find(y)){
        up[find(x)]=find(y);
        return true;
    }
    return false;
}
⑷初始化
idx=0;MST=0;
for(int i=1;i<=n;i++) up[i]=i;
⑸排序std::sort(edges+1,edges+idx+1);
⑹算法核心
for(int i=1;i<=idx;i++)
    if(join(edges[i].x,edges[i].y)) MST+=edges[i].v;

 然后就是洛谷模板题。

https://www.luogu.org/problemnew/show/P3366

#include<iostream>
#include<algorithm>
#include<cstdio>
//Kruskal
using namespace std;

struct edge{
    int x,y,v;    
}edges[210000]; 
bool compare(const edge &eg1,const edge &eg2){
    return eg1.v<eg2.v;
}
int n,m,a,b,c,up[5005],idx,MST;
int find(int x){
    if(up[x]!=x){
        up[x]=find(up[x]);
    }
    return up[x];
}
bool join(int x,int y){
    if(find(x)!=find(y)){
        up[find(x)]=find(y);
        return true;
    }
    return false;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
        scanf("%d%d%d",&a,&b,&c);
        edges[++idx].x=a;
        edges[idx].y=b;
        edges[idx].v=c;
    }
    sort(edges+1,edges+idx+1,compare);
    for(int i=1;i<=n;i++){
        up[i]=i;
    }
    for(int i=1;i<=idx;i++){
        if(join(edges[i].x,edges[i].y)){
            MST+=edges[i].v;
        }
    }
    printf("%d\n",MST);
}