最小生成树与Prim算法

最小生成树（MST）

定义

首先是一棵树（废话

其次没有回路（废话

包含全部顶点和V-1条边

边的权重和最小！！！！！

所以如果是单棵最小生成树，至少说明图是连通的。不然就是森林。

生成思路

既然是根据图生成树，那么至少要有遍历图。那么，便要从一个源点出发，来一场愉快的深搜或广搜。

深搜生成就叫DFS树（深度优先搜索树

广搜生成就叫BFS树（广度优先搜索树

我们只需要在if语句中，在递归调用语句之前做一点手脚，便可以达到目的。

Prim算法——让一棵小树长大

（别装了！Dijkstra我知道是你！）

时间复杂度

O（n^2），是根据图生成最小树的算法。

算法思路

是一个穿了马甲的Dijkstra算法。用的是蓝白点的思想。

Dijkstra是啥？https://www.cnblogs.com/Uninstalllingyi/p/10417446.html

每次循环都把一个蓝点u变成白点。并且这个蓝点u与白点相连的边权势当前所有蓝点中最小的min[u]

仔细想想，是贪心的思路哟…

好的，我们来手工模拟一下。求下面这个图的最小生成树。（里面是伪代码哟）

（emm…其实这个是绿白点…没事你就假装一下色盲。）

初始所有的点全都是蓝点，所以说这里有一个数组min[i]来表示一下。那么除了起点，其他的全部初始化为无穷大(0x3f)。即min[1]=0。权值之和用int MST=0来保存。

那么第一次循环就没什么说的了，min[1]=0是最小的蓝点，然后把1变白。然后枚举和a相连的蓝点，修改它们与白点相连的最小边权（就是min数组啦）

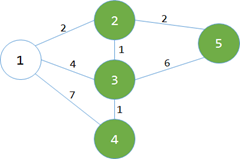
min[2]=map[1][2]=2;
min[3]=map[1][3]=4;
min[4]=map[1][4]=7;

第二次循环找到min[2]是最小的蓝点，变白。然后更新相连的蓝点。bulabulabula。

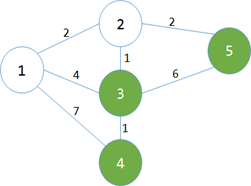
min[3]=map[2][3]=1; min[5]=map[2][5]=2;

第三次循环…找到min[3]=1是最小的那个…变白…更新蓝点最小值…

 

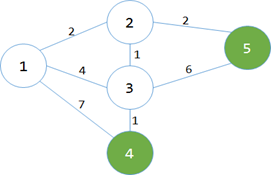
min[4]=map[3][4]=1;

哦，这里要注意一下，因为min[5]=2<6，所以5不用更新。

 第四次循环找到点4，第五次循环找到点5.反正他们也没相连的蓝点了，所以直接变白叭。

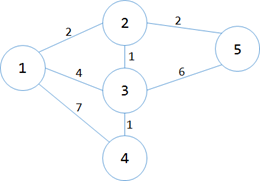
那么，最后得到的权值之和是…

min[1]+min[2]+min[3]+min[4]+min[5]=
0+2+1+1+2=6;

以1为起点生成最小生成树,min[v]表示蓝点与白点相连的最小边权。
MST表示最小生成树的权值之和。
⑴初始化min[v]=∞(v≠1);min[1]=0;MST=0;
⑵for(int i=1;i<=n;i++){
        ①寻找min[u]最小的蓝点u
        ②将u标记为白点
        ③MST+=min[u]
        ④for(int v=1;v<=n;v++)//与白点u相连的所有蓝点v
            if(w[u][v]<min[v]) min[v]=w[u][v]//注:w[u][v]表示第u行第v个元素。第u行表示和白点u相连的所有的点。
}
⑶算法结束,MST即为最小生成树的权值之和。

这里有一道洛谷的模板题

https://www.luogu.org/problemnew/show/P3366

#include<iostream>
#include<cstring>
#include<cstdio>
//prim算法 
using namespace std;
const int maxx=0x3f3f3f3f;
const int MAXN=5005;
int n,m,x,y,z,map[MAXN][MAXN],minn[MAXN],MST=0,vis[MAXN];
int main(){
     scanf("%d%d",&n,&m);
     memset(map,0x3f,sizeof(map));
     for(int i=1;i<=m;i++){
         scanf("%d%d%d",&x,&y,&z);
         if(map[x][y]>z){
             map[x][y]=map[y][x]=z;
         }
     }
     memset(minn,0x3f,sizeof(minn));
     minn[1]=0;
     for(int i=1;i<=n;i++){
         int u=0;
         for(int j=1;j<=n;j++){
             if(!vis[j]&&minn[u]>minn[j]){
                 u=j;
             }
         }
         vis[u]=true;
         MST+=minn[u];
         for(int v=1;v<=n;v++){
             if(!vis[v]&&map[u][v]<minn[v]){
                 minn[v]=map[u][v];
             }
         }
     }
     printf("%d\n",MST);
      
}

（倒是头一次知道洛谷如果不加cstdio的头文件是不可以用printf的…尴尬。