枢轴量法、分位数

Part 1：枢轴量法

枢轴变量法是基于点估计量的。我们知道，统计量是样本的函数，这意味着统计量中不能含有未知参数，而参数的点估计量是用统计量的观测值作为待估参数的估计值，其分布一定含有待估参数，枢轴量法的思想就是，通过一定的变换，让点估计的函数的分布不含待估参数，进而基于分布来构造区间估计。

举一个简单的例子，对于正态总体N(μ,4)N(μ,4)，显然X¯∼N(μ,4/n)X¯∼N(μ,4/n)，这里X¯X¯的分布含有未知参数μμ。构造其枢轴量，就是找到一个函数变换，使得新的随机变量分布不含未知参数。注意，这里用了随机变量这个词而不是统计量，意味着枢轴量不是统计量，即不能由样本观测值计算出，这是因为虽然枢轴量的分布不含未知参数，但是枢轴量的表现形式含有未知参数。显然，这里

 

X¯−μ∼N(0,4n),X¯−μ∼N(0,4n),

 

这样，X¯−μX¯−μ的分布已知，自然容易找到一个常数区间[c,d][c,d]，使得这个区间有1−α1−α的概率包含X¯−μX¯−μ的观测值，虽然此时我们不知道区间的端点是多少，但至少知道端点可以是固定的数c,dc,d。对枢轴量使用不等式变换，即X¯−μ∈[c,d]⇒μ∈[X¯−d,X¯−c]X¯−μ∈[c,d]⇒μ∈[X¯−d,X¯−c]，得到置信水平为1−α1−α的置信区间。这就是枢轴量法的操作步骤。

不同分布族的参数对于总体的意义是不同的。像正态分布N(μ,σ2)N(μ,σ2)的均值μμ，均匀分布U(a,a+r)U(a,a+r)的起点aa这种参数主要影响观测值的大小，可以直接通过X−μX−μ，X−aX−a的手段消除，这种参数称为位置参数；正态分布N(μ,σ2)N(μ,σ2)的标准差σσ，指数分布E(λ)E(λ)的速率λλ这种参数主要影响观测值的离散程度，可以通过X/σX/σ，λXλX之类的手段消除，这种参数称为尺度参数。面对不同的参数，往往有不同的方式构造枢轴量，应当结合其特点选择构造方式。

接下来，我们将枢轴量法运用到一些具体实例中，体会枢轴量法的实际应用。

Part 2：分位数

在开始枢轴量法的实际应用前，先介绍分位数这一概念，这为我们确定置信区间提供了有力武器。现在，我们先给出分位数的定义（如果不特别说明，都指总体分位数而非样本分位数）。分位数可以分为下分位数和上分位数，一般称下分位数为分位数，但我们更常用的是上分位数。

对于某个分布FF，X∼FX∼F，FF的（下）αα分位数指的是这样一个点xαxα，满足

 

P(X≤xα)=α,P(X≤xα)=α,

 

如果FF有反函数F−1(x)F−1(x)，则有xα=F−1(α)xα=F−1(α)。

对于某个分布FF，X∼FX∼F，FF的上αα分位数指的是这样一个点yαyα，满足

 

P(X≥yα)=α.P(X≥yα)=α.

 

换言之，如果分布函数FF存在反函数F−1(x)F−1(x)，则FF的上αα分位数是yα=F−1(1−α)yα=F−1(1−α)。

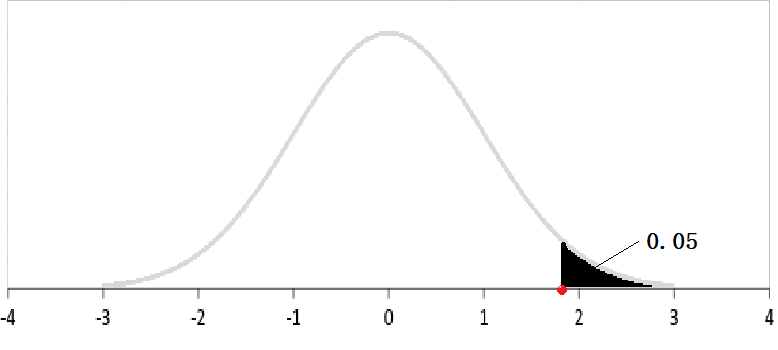
也许结合图形会更好理解。对于上面的图形，如果这是一个密度函数，黑色部分的面积为0.050.05，那么红色的点就是该分布的上0.050.05分位数，同时也是其下0.950.95分位数。

显然，对于一个完全确定的分布，其各分位数都是完全确定的，是常数。分布多种多样，不可能对所有分布都详细地讨论其分位数，但是对一些常用分布，其各分位数的数值已经被制成表，这包括标准正态分布，与正态分布的三大衍生分布——χ2χ2分布、tt分布、FF分布。

今后，我们将使用uαuα、χ2α(n)χα2(n)、tα(n)tα(n)、Fα(m,n)Fα(m,n)，分别代表标准正态分布、自由度为nn的χ2χ2分布、自由度为nn的tt分布、自由度为m,nm,n的FF分布的上αα分位数，给定分布类型、分位、自由度后，这些值都可以通过查阅分位数表得到。

__EOF__

本文作者：lishuaics
本文链接：https://www.cnblogs.com/L-shuai/p/15435060.html
关于博主：IT小白
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！