插头dp
插头dp是什么,这里只有插头

在状态压缩动态规划中,有一类是需要记录若干个元素的联通情况,称之为基于连通性状态压缩的动态规划,也就是插头 dp
在大部分棋盘状压 dp 中,状态划分可以依据行或列进行划分,行列之间相对独立,但有时却不行,例如让你在棋盘中对联通块进行操作,下图的联通块是无法用上述的方法去记录的
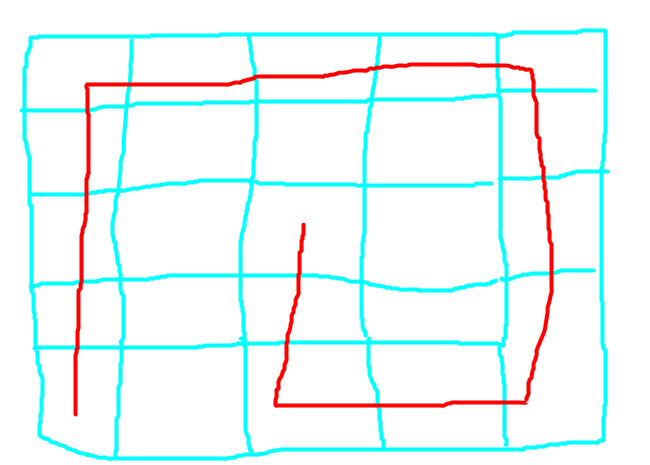
这时便不能采用上述做法,只能考虑新做法
先讲几个概念
1.插头:对于一个4连通的问题来说,它通常有上下左右4个插头,一个方向的插头存在表示这个格子在这个方向可以与外面相连
2.轮廓线:已决策状态和未决策状态的分界线
插头 dp 处理一条回路问题
考虑一题
给出 \(n\times m\) 的方格,有些格子不能铺线,其它格子必须铺,形成一个闭合回路。问有多少种铺法?(P5056)
我们发现一个格子若在联通块内,则 4 个插头恰好有 2 个插头存在,即从一个格子进来,另一个格子出去,考虑一种逐格递推形式,则轮廓线会发生如下变化
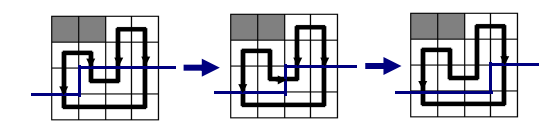
考虑轮廓线应记录插头,分析一下轮廓线上的插头位置
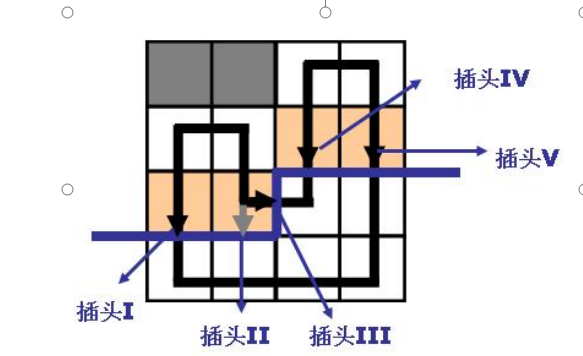
这很好理解,轮廓线一下是未决策的点,已经决策的点都可以向未决策的点有一个插头
这已经很好的给出了状态转移方程的思路,令 \(dp_{i,j,S_0}\) 为到了 第 \(i\) 行,第 \(j\) 列,所有插头状态为 \(S_0\)
考虑 \(S_0\) 如何记录,如何表示
,先考虑回路的特点
以上图为例,轮廓线上方是由若干条互不相交的路径构成的,而每条路径的两个端口恰好对应了轮廓线上的两个插头,一条路径上的所有格子对应的是一个连通块,而每条路径的两个端口对应的两个插头是连通的而且不与其他任何一个插头连通,也就是说,在任何时候每一个连通分量恰好有2个插头,在考虑一条性质
轮廓线上从左到右4个插头 \(a,b, c, d\),如果 \(a, c\) 连通,并且与 \(b\) 不连通,那么 $ b, d$ 一定不连通
证明引用陈丹琦的论文

“两两匹配”,“不会交叉”这样的性质,我们很容易联想到括号匹配,则一条轮廓线之间,左插头一定可以与右插头一一对应,那么考虑一种括号表示法,用0表示无插头,1表示左括号插头,2表示右括号插头来记录下所有的轮廓线信息
这样,状态的储存也表示完毕,考虑如何转移,按格转移,令 \((i,j-1)\) 的右插头为 \(p\),\((i-1, j)\) 的下插头为 \(q\),$ (i, j)$ 的下插头为 \(x\),右插头为 \(y\),每次转移就是将 \(p\) ,\(q\) 改为 \(x\) ,\(y\)
-
\((i,j)\) 为障碍,显然不能有插头,即只有 \(p=0,q=0\) 才能转移至 \(x=0,y=0\)
-
新建一个插头,即 \(p,q=0\) 时令 \(x=1,y=2\)
-
只有向右插头,即 \(p\) 不为 \(0\) 且 \(q\) 为 \(0\) 时,由于没有可接的插头,只能将右插头延伸,可直走可拐弯,即 \(x=1,y=0\) 或 \(x=2,y=0\)
-
只有向下插头,同上,令 \(x=0,y=1\) 或 \(x=0,y=2\)
-
向右为左插头,向下为右插头,考虑从插头建立到最后闭合,显然是一个闭合回路,这种情况只能在最后一次转移出现,也只有这种情况能计入答案
-
向右为右插头,向下为左插头,则合并插头之后,该右插头对应的左插头和该左插头对应的右插头在消掉之后恰好匹配,也不需要执行其他改动,即令 \(x=0,y=0\)
-
两个都是左插头,在合并之后应将两个右插头对应的左插头设为匹配
-
两个都是右插头,在合并之后应将两个左插头对应的右插头设为匹配
对于找插头来说,之间进行括号匹配即可
将每次的状态都推向下一次决策点,发现对于下一次决策点来说,可能有极多的状态,考虑简化,可以发现,轮廓线相同的之后的转移是一致的,则可以将推向下一次决策点的状态存进一个哈希表,每次取出哈希表中的状态即可实现合并状态,实现如下
void insert(int sta,int val)//sta为轮廓线状态,val为该状态的方案数
{//考虑状态本质上是这次到下次,不妨用滚动数组优化空间,令 now 为下次要用的状态所属的哈希表,则下次决策点令now取反,则上次的数组被下下次复用
int key=sta%mod+1;
for(int i=head[key];i;i=nxt[i])//挂表法哈希,学过链式前向星的也可看做向 $key$ 点建一条边
{
if(e[now][i].sta==sta)
{
e[now][i].val+=val;
return ;
}
}
e[now][++cnt[now]]={sta,val};
nxt[cnt[now]]=head[key];
head[key]=cnt[now];
}
由于 插头 dp 的实现比较困难,下文将给出一步步的过程
1.找到能统计答案的点,即最后一个非障碍点,边读入边处理,若为非障碍点,直接更新最后一个非障碍点即可
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
char c;cin>>c;
if(c!='.') continue;
a[i][j]=1;x=i;y=j;
}
}
2.初始化和状态实现,初始化直接向哈希表插入 \((0,1)\), 考虑三进制(0,1,2)不好写,直接用四进制实现,顺便初始化四次幂,可以发现四进制右移一位,即为二进制中 \(x<<2\),为了转移方便,令 \(last\) 为上次决策点,\(now\) 为这次决策点,正在进行这次决策
bit[0]=1;
last=0;now=1;
for(int i=1;i<=13;++i)
{
bit[i]=bit[i-1]<<2;
}
insert(0,1);
3.上一行向下一行转移,当按格转移到头,考虑换下一行,如下
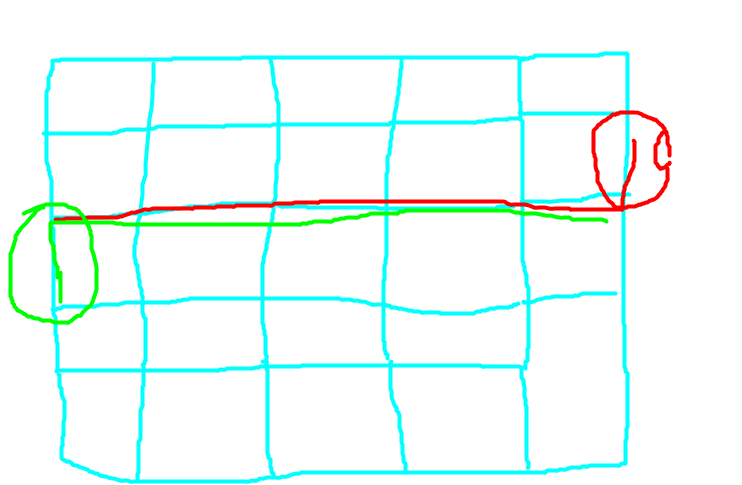
可以发现,红圈的插头已经无用,绿圈的插头是新出现的,显然为 0
其他位置直接继承,综上,对红线所对应的状态整体左移一位(四进制下),就是绿线
for(int j=1;j<=cnt[now];++j)
{
e[now][j].sta<<=2;
}
4.状态实际表示和转移
以从左到右的顺序依次标记为 \(0,1,...,n\) 共 \(n+1\) 个插头的编号,这状态为 \(sta\) ,则 (i,j) 的右插头为四进制下第 \(j-1\) 位,下插头为四进制下第 \(j\) 位,同时从 \((i,j-1)\) 到 \((i,j)\) 时,应将 \(last\) 与 \(now\) 交换,哈希表初始为 0,再将 \(last\) 中所有状态依次遍历即可
for(int j=1;j<=m;++j)
{
memset(head,0,sizeof(head));
swap(last,now);cnt[now]=0;
for(int k=1;k<=cnt[last];++k)
{
int sta=e[last][k].sta,num=e[last][k].val;
int b1=(sta>>(2*(j-1)))%4;//左插头
int b2=(sta>>(2*j))%4;//下插头
if(a[i][j]==0)
{
if(b1==0&&b2==0) insert(sta,num);
}
else if(b1==0&&b2==0)
{
if(a[i+1][j]&&a[i][j+1]) insert(sta+bit[j-1]+2*bit[j],num);
}
else if(b1==0&&b2)
{
if(a[i][j+1]) insert(sta,num);
if(a[i+1][j]) insert(sta-bit[j]*b2+bit[j-1]*b2,num);
}
else if(b1&&b2==0)
{
if(a[i+1][j]) insert(sta,num);
if(a[i][j+1]) insert(sta-bit[j-1]*b1+bit[j]*b1,num);
}
else if(b1==1&&b2==1)//找b2的右插头
{
int k1=1;//当k1=0时当前点为b2的右插头
for(int l=j+1;l<=m;++l)
{
if((sta>>(2*l))%4==1) k1++;//碰到一个左括号就++
if((sta>>(2*l))%4==2) k1--;//碰到一个左括号就--
if(k1==0) {insert(sta-bit[j-1]-bit[j]-bit[l],num);break;}
}
}
else if(b1==2&&b2==2)//找b1的左插头
{
int k2=1;
for(int l=j-2;~l;--l)
{
if((sta>>(2*(l)))%4==1) k2--;
if((sta>>(2*(l)))%4==2) k2++;
if(k2==0) {insert(sta-bit[j-1]*2-bit[j]*2+bit[l],num);break;}
}
}
else if(b1==2&&b2==1)
{
insert(sta-bit[j-1]*b1-bit[j]*b2,num);
}
if(i==x&&j==y) ans+=num;
}
总代码如下
点击查看代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<vector>
#include<queue>
#include<cmath>
#define int long long
using namespace std;
int read()
{
int s=0,w=1;
char c=getchar();
while(c>57||c<48)
{
if(c=='-1') w=-1;
c=getchar();
}
while(c>47&&c<58)
{
s*=10;
s+=c-48;
c=getchar();
}
return w*s;
}
void print(long long x)
{
if(x<0)
{
x=-x;
putchar('-');
}
if(x>9) print(x/10);
putchar(x%10+48);
}
struct node{
int sta,val;
}e[2][2<<24];
int head[3001000],nxt[2<<24],last,now,cnt[5],mod=299987;
void insert(int sta,int val)
{
int key=sta%mod+1;
for(int i=head[key];i;i=nxt[i])
{
if(e[now][i].sta==sta)
{
e[now][i].val+=val;
return ;
}
}
e[now][++cnt[now]]={sta,val};
nxt[cnt[now]]=head[key];
head[key]=cnt[now];
}
int n,m;
int a[20][20];
int bit[19],ans=0,x,y;
signed main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
char c=getchar();
while(c!='*'&&c!='.') c=getchar();
if(c!='.') continue;
a[i][j]=1;x=i;y=j;
}
}
bit[0]=1;
last=0;now=1;
for(int i=1;i<=13;++i)
{
bit[i]=bit[i-1]<<2;
}
insert(0,1);
for(int i=1;i<=n;++i)
{
for(int j=1;j<=cnt[now];++j)
{
e[now][j].sta<<=2;
}
for(int j=1;j<=m;++j)
{
memset(head,0,sizeof(head));
swap(last,now);cnt[now]=0;
for(int k=1;k<=cnt[last];++k)
{
int sta=e[last][k].sta,num=e[last][k].val;
int b1=(sta>>(2*(j-1)))%4;
int b2=(sta>>(2*j))%4;
if(a[i][j]==0)
{
if(b1==0&&b2==0) insert(sta,num);
}
else if(b1==0&&b2==0)
{
if(a[i+1][j]&&a[i][j+1]) insert(sta+bit[j-1]+2*bit[j],num);
}
else if(b1==0&&b2)
{
if(a[i][j+1]) insert(sta,num);
if(a[i+1][j]) insert(sta-bit[j]*b2+bit[j-1]*b2,num);
}
else if(b1&&b2==0)
{
if(a[i+1][j]) insert(sta,num);
if(a[i][j+1]) insert(sta-bit[j-1]*b1+bit[j]*b1,num);
}
else if(b1==1&&b2==1)
{
int k1=1;
for(int l=j+1;l<=m;++l)
{
if((sta>>(2*l))%4==1) k1++;
if((sta>>(2*l))%4==2) k1--;
if(k1==0) {insert(sta-bit[j-1]-bit[j]-bit[l],num);break;}
}
}
else if(b1==2&&b2==2)
{
int k2=1;
for(int l=j-2;~l;--l)
{
if((sta>>(2*(l)))%4==1) k2--;
if((sta>>(2*(l)))%4==2) k2++;
if(k2==0) {insert(sta-bit[j-1]*2-bit[j]*2+bit[l],num);break;}
}
}
else if(b1==2&&b2==1)
{
insert(sta-bit[j-1]*b1-bit[j]*b2,num);
}
if(i==x&&j==y) ans+=num;
}
}
}
print(ans);
return 0;
}
插头 dp处理一条路径问题
考虑一种路径问题,给你一个 \(m*n\) 的棋盘,有的格子是障碍,要求从一个非障碍格子出发经过每个非障碍格子恰好一次,问方案总数
这个问题是一条路径,而不是一条回路,也就是说,轮廓线上的插头,会出现与其他插头不匹配的插头,不妨称之为独立插头,这样插头就有了四种状态(将 \(3\) 记为独立插头),转移部分与上述一致,只讨论与独立插头的转移
仍使用 \(p,q,x,y\) 为标记
-
\(p=0\) , \(q=0\),考虑除了左右插头,还要考虑独立插头的生成,即 \(x=0,y=3\) 或 \(x=3,y=0\)
-
\(p=3,q=3\),记独立插头合并,此时路径闭合,所以只能在最后一次转移出现
-
存在一个独立插头,若另一个为左插头或右插头,即当前左插头或右插头都会被改成独立路径,即将该左插头或右插头对应的左插头或右插头改为独立插头,若无插头,直接延伸即可,或到了最后一次转移,独立插头即可作为路径一端
-
如果只有左插头或右插头,除了延伸,也可强行封住插头,即将它变为独立插头,则该插头与对应的插头都应变为独立插头
最后注意,任何时候轮廓线上独立插头的个数不可以超过2个,否则会出现多个联通块
如果没有 L 的限制,则是模板题,而有了 L ,便不好 dp,考虑观察一条路径
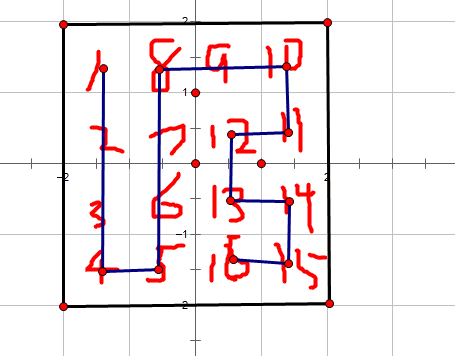
当对路径上每个点编号,则有几条性质
-
连通性只有 小的向大的联通,大的向小的联通,不妨分别即为插头 1 和插头 2
-
1 只有插头 1,末尾只有插头 2,其他节点分别有 插头 1 和 插头 2
考虑对轮廓线上每个位置填编号,再考虑插头是什么,但保证编号不重复却很难写,考虑如下性质,一个轮廓线中,如果所有插头和填的编号都相同,则已经填的数的集合相同,则可以对每个轮廓线开一个 bitset 存下每个数是否出现过,则对于每个轮廓线来说,有四个插头,三个数,一个 bitset,将 32 位分成四个八位,一个存插头,三个存数,至此状态问题解决,考虑转移,仍令 \((i,j-1)\) 的右插头为 \(p\),\((i-1, j)\) 的下插头为 \(q\),$ (i, j)$ 的下插头为 \(x\),右插头为 \(y\)
-
\(p=0\) 和 \(q=0\),可以放入 1 和一个递增插头,也可放入 n*m 和一个递减插头,亦可放入其他数和一个递增和一个递减
-
\(p=0\) 和 $q \ne 0 $ ,考虑延伸 插头 q 即可,注意如果填的数为 1 或 n*m ,则需封闭插头
-
\(p \ne0\) 和 $q = 0 $ ,同上
-
\(p+q=3\) 即插头合并,此时必须满足左边的数和上边的数相差为 2,且小的必须连递增插头,大的为递减插头,可以转移
还有一些通用条件
-
最右不能连右插头,最下不能连下插头
-
填 1 时注意是否在边界
3.填的数之前不能出现,且须符合 L 数组的限制
插头 dp处理一类染色问题
仍然考虑先观察一种染色方案
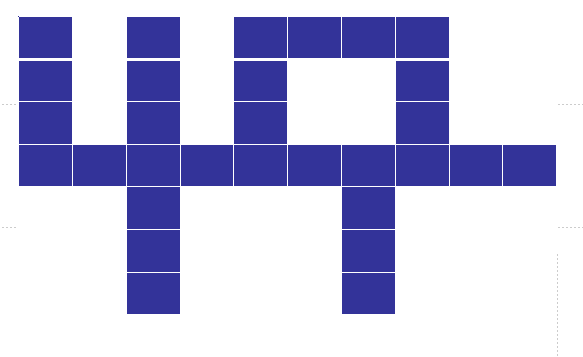
可以发现被染色的和其他格子联通的,如果用轮廓线去扫,在轮廓线之上是若干个联通块,考虑记录他们的连通性,具体的,我们可以维护轮廓线上每个格子的连通性,每次尝试加入一个新格子,在维护连通性上,可以采用最小表示法,一种最小表示法为:所有的没选的标记为 0,第一个选的格子以及与它连通的所有格子标记为 1,然后再找第一个选的的非障碍格子以及与它连通的格子标记为 2,……,重复这个过程,直到所有的格子都标记完毕
在状态表示完毕之后,应依据左边和右边格子的状态(不是插头),来计算当前是否选格子,转移如下
-
左和上都为 0,则可以选择选或不选这个格子
-
左不为 0,上为 0,则可以选择延伸或不延伸这个格子
-
左为 0,上不为 0,则可以选择延伸或不延伸这个格子,但要注意,如果上格子与其他格子都不是一个联通块,则必须延伸格子,否则会出现一个孤立的联通块
-
左不为 0,上不为 0,应合并两个格子及所有联通格子,或者不合并直接断开,仍要注意断开时上格子的特判
点击查看代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<string>
#include<cstring>
#include<bitset>
#define int long long
using namespace std;
int n;
int a[20][20];
int bit[20];
struct node{
int sta,val;
}e[3][6400100];
int nxt[6400100],head[6400100],cnt[3],mod=299998;
int now=1,last,ans=-1e9+7;
int vis[20];
int build(int x,int v)
{
memset(vis,0,sizeof(vis));
int sum=0,cnt=0;
for(int p=1;p<=n;p++)
{
if(!vis[p])
{
int to=(x>>((p-1)*3ll))%8;
if(to!=0) cnt++;
for(int i=p;i<=n;i++)
{
int bi=(x>>((i-1)*3ll))%8;
if(to==bi)
{
vis[i]=1;
if(to!=0) sum=sum+bit[i-1]*cnt;
}
}
}
}
if(cnt==1) ans=max(ans,v);
return sum;
}
void insert(int x,int v)
{
x=build(x,v);
int k=x%mod+1;
for(int i=head[k];i;i=nxt[i])
{
if(e[now][i].sta==x)
{
e[now][i].val=max(e[now][i].val,v);
return ;
}
}
e[now][++cnt[now]]={x,v};
nxt[cnt[now]]=head[k];head[k]=cnt[now];
}
signed main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cin>>a[i][j];ans=max(ans,a[i][j]);
}
}
bit[0]=1;
for(int i=1;i<=10;i++)
{
bit[i]=bit[i-1]*8;
}
insert(0,0);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
swap(now,last);
memset(head,0,sizeof(head));cnt[now]=0;
for(int k=1;k<=cnt[last];k++)
{
int sta=e[last][k].sta,v=e[last][k].val;
int b1=(j==1?0:(sta>>((j-2)*3ll))%8),b2=(sta>>((j-1)*3ll))%8;
if(b1==0&&b2==0)
{
insert(sta,v);
insert(sta+bit[j-1]*7,v+a[i][j]);
}
if(b1!=0&&b2==0)
{
insert(sta,v);
insert(sta+bit[j-1]*b1,v+a[i][j]);
}
if(b1==0&&b2!=0)
{
insert(sta,v+a[i][j]);
bool f=0;
for(int p=1;p<=n;p++)
{
int bi=(sta>>((p-1)*3ll))%8;
if(p!=j&&b2==bi) f=1;
}
if(f==1) insert(sta-bit[j-1]*b2,v);
}
if(b1!=0&&b2!=0)
{
int to_sta=sta,k1=b1,k2=b2;
for(int p=1;p<=n;p++)
{
int bi=(sta>>((p-1)*3ll))%8;
if(bi==k1||bi==k2) to_sta=to_sta-bit[p-1]*bi+bit[p-1]*7;
}
insert(to_sta,v+a[i][j]);
bool f=0;
for(int p=1;p<=n;p++)
{
int bi=(sta>>((p-1)*3ll))%8;
if(p!=j&&b2==bi) f=1;
}
if(f==1) insert(sta-bit[j-1]*b2,v);
}
}
}
}
cout<<ans;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号