离线分治学习笔记
分治在数集维护上用处很大,常用的是 cdq 分治,整体二分,线段树分治
所有的分治之所以能优化,是因为分治能最大化各个询问间的重复操作,将重复操作只算一次,而利用的原理就是分治原理(只要保证任意两个操作和询问间的相对时序不变,我们就可以任意处理这个操作-询问序列)
cdq 分治
基本思想
-
将区间 \(l\) 到 \(r\) 分成 \(l\) 到 \(mid\) 和 \(mid+1\) 到 \(r\)
-
递归处理左右两边
-
统计左边对右边的贡献
可以解决 \(3\) 类问题
-
解决和偏序有关的问题
-
1D/1D 动态规划的优化与转移
-
一些动态问题转化为静态问题
先对第一维排序,再分治第二维
回溯时需用双指针统计左边对右边的贡献,流程如下
先对左右两边按第二维分别排序,在左右两边各放一个指针,若右边对应的值大于左边,则将左边的指针向右移一位,直到不能移动为止,可知当右边指针向后移动时,左边的指针及其之前的值第二维都小于新指的值
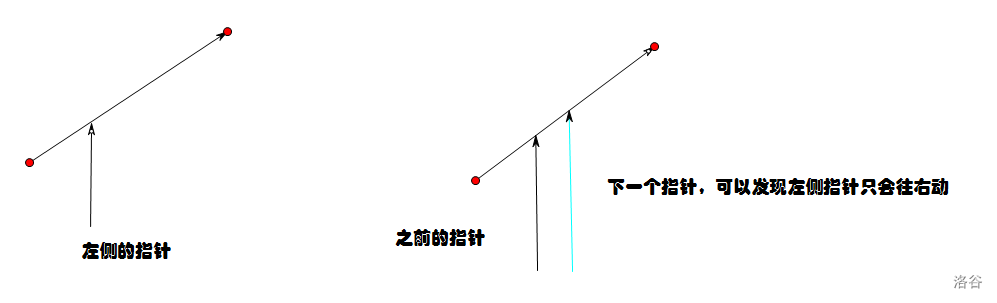
此时对于每个右指针,左指针及其之前的数都前两维小于右指针,偏序只可能在这之间产生,考虑使用树状数组维护,只需单点加,查询前缀和即可
对于这题,应先排序去重,再进行分治,对于一个 有 \(ans\) 个不同的偏序,\(sum\) 个相同的数,则在
\(ans+sum-1\) 处贡献了 \(sum\) 个值,处理一下即可
点击查看代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<string>
#include<cstring>
using namespace std;
struct node{
int a,b,c,num,ans;
}in[200100],sol[200100];
int n,Max,m,rt,id,sum[200100];
int c[200100];
int lowbit(int x)
{
return x&(-x);
}
void add(int x,int y)
{
while(x<=Max)
{
c[x]+=y;
x+=lowbit(x);
}
}
int query(int x)
{
int sum=0;
while(x)
{
sum+=c[x];
x-=lowbit(x);
}
return sum;
}
bool cmp1(node x,node y)
{
if(x.a==y.a&&x.b==y.b) return x.c<y.c;
else if(x.a==y.a) return x.b<y.b;
return x.a<y.a;
}
bool cmp2(node x,node y)
{
if(x.b==y.b) return x.c<y.c;
return x.b<y.b;
}
void cdq(int li,int ri)
{
if(li==ri) return ;
int mid=(li+ri)>>1;
cdq(li,mid);cdq(mid+1,ri);
sort(sol+li,sol+mid+1,cmp2);
sort(sol+mid+1,sol+ri+1,cmp2);
int i=li,j=mid+1;
for(;j<=ri;j++)
{
while(sol[i].b<=sol[j].b&&i<=mid)
{
add(sol[i].c,sol[i].num);
i++;
}
sol[j].ans+=query(sol[j].c);
}
for(int k=li;k<i;k++)
{
add(sol[k].c,-sol[k].num);
}
rt=id=0;
}
int main()
{
cin>>n>>Max;
for(int i=1;i<=n;i++)
{
cin>>in[i].a>>in[i].b>>in[i].c;
}
sort(in+1,in+1+n,cmp1);
int top=0;
for(int i=1;i<=n;i++)
{
top++;
if(in[i].a!=in[i+1].a||in[i].b!=in[i+1].b||in[i].c!=in[i+1].c)
{
m++;
sol[m]={in[i].a,in[i].b,in[i].c,top,0};
top=0;
}
}
cdq(1,m);
for(int i=1;i<=m;i++)
{
sum[sol[i].ans+sol[i].num-1]+=sol[i].num;
}
for(int i=0;i<n;i++)
{
cout<<sum[i]<<endl;
}
return 0;
}
对于 1D/1D 问题( DP 数组是一维的,转移是 \(O(n)\) 的),有时可以用 \(cdq\) 分治来优化,如二维最长上升子序列如下:
\(dp_{i}=1+ \max_{j=1}^{i-1}dp_{j}[a_{j}<a_{i}][b_{j}<b_{i}]\)
因为二维偏序才能转移,且加上时间一维正好三维,想法是套用上述的解法,只不过将统计改成转移
但是它必须满足两个条件,否则就是不对的:
用来计算 \(dp_{i}\) 的所有 \(dp_{j}\) 值都必须是已经计算完毕的,不能存在半成品;
用来计算 \(dp_{i}\) 的所有 \(dp_{j}\) 值都必须能更新到 \(dp_{i}\) ,不能存在没有更新到的 \(dp_{j}\) 值
综上,在统计时,必须夹在 \(solve(l,mid)\) , \(solve(mid+1,r)\) 的中间
可以发现长度的 dp 式与上文一样不再考虑,但本题要求出概率,考虑概率是当前方案除以总方案,可以求出方案数,十分的套路
令 \(f1[i],f2[i]\) 为以 \(i\) 为开头或结尾的最长上升子序列的长度,\(g1[i],g2[i]\) 为对应的方案数,正反跑两边 cdq 可以解决
点击查看代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<vector>
#include<string>
#include<cstring>
#include<set>
#define int long long
using namespace std;
struct node{
int h,v,pre;
}a[640100],b[640010],c[640010];
int n;
int f1[640010],f2[640010];
long double g1[640010],g2[640010],c2[640010],sum;
int c1[640010],lsv[640010],cnt;
int maxn;
int lowbit(int x){return x&(-x);}
void add(int x,int k1,long double k2)
{
for(int i=x;i;i-=lowbit(i))
{
if(k1<0) c1[i]=0,c2[i]=0.0;
else
{
if(c1[i]<k1) c1[i]=k1,c2[i]=k2;
else if(c1[i]==k1) c2[i]+=k2;
}
}
}
void query(int x,int now,int opt)
{
int ans1=0;
long double ans2=0;
for(int i=x;i<=n;i+=lowbit(i))
{
if(ans1<c1[i]) ans1=c1[i],ans2=c2[i];
else if(ans1==c1[i]) ans2+=c2[i];
}
if(opt==1)
{
if(f1[now]<ans1+1) f1[now]=ans1+1,g1[now]=ans2;
else if(f1[now]==ans1+1) g1[now]+=ans2;
}
if(opt==2)
{
if(f2[now]<ans1+1) f2[now]=ans1+1,g2[now]=ans2;
else if(f2[now]==ans1+1) g2[now]+=ans2;
}
}
bool cmp(node x,node y)
{
return x.h>y.h;
}
void cdq(int L,int R,int opt)
{
if(L==R) return ;
int mid=(L+R)>>1,l=L,r=mid+1;
cdq(L,mid,opt);
sort(a+L,a+mid+1,cmp);
for(int i=r;i<=R;i++) b[i]=a[i];
sort(a+mid+1,a+R+1,cmp);
for(int i=r;i<=R;i++)
{
while(l<=mid&&a[l].h>=a[i].h)
{
if(opt==1) add(a[l].v,f1[a[l].pre],g1[a[l].pre]);
else add(a[l].v,f2[a[l].pre],g2[a[l].pre]);
l++;
}
query(a[i].v,a[i].pre,opt);
}
for(int i=L;i<l;i++)
{
add(a[i].v,-1,-1);
}
for(int i=r;i<=R;i++) a[i]=b[i];
cdq(mid+1,R,opt);
}
signed main()
{;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i].h>>a[i].v;c[i]=a[i];a[i].pre=i;
lsv[i]=a[i].v;
f1[i]=f2[i]=1;g1[i]=g2[i]=1;
}
sort(lsv+1,lsv+1+n);cnt=unique(lsv+1,lsv+1+n)-lsv-1;
for(int i=1;i<=n;i++)
{
a[i].v=lower_bound(lsv+1,lsv+1+cnt,a[i].v)-lsv;
}
cdq(1,n,1);
for(int i=1;i<=n;i++)
{
if(f1[i]>maxn) maxn=f1[i],sum=g1[i];
else if(f1[i]==maxn) sum+=g1[i];
}
reverse(c+1,c+1+n);
for(int i=1;i<=n;i++)
{
a[i].h=-c[i].h;a[i].v=-c[i].v;lsv[i]=-c[i].v;a[i].pre=i;
}
sort(lsv+1,lsv+1+n);cnt=unique(lsv+1,lsv+1+n)-lsv-1;
for(int i=1;i<=n;i++)
{
a[i].v=lower_bound(lsv+1,lsv+1+cnt,a[i].v)-lsv;
}
cdq(1,n,2);
cout<<maxn<<endl;
for(int i=1;i<=n;i++)
{
if(f1[i]+f2[n-i+1]-1==maxn)
{
printf("%.5Lf ",g1[i]/sum*g2[n-i+1]);
}
else cout<<"0.00000 ";
}
fclose(stdin);
fclose(stdout);
return 0;
}
cdq 分治更常用的是将动态问题转化为静态问题,需满足以下要求
-
题目所有操作能以时间顺序有序进行,且不会对后续时间造成影响
-
只有插入或只有删除,且该插入或删除只对后面询问造成影响
-
静态问题是可做的,且题目允许离线
举个例子,如维护一个二维平面,然后支持在一个矩形区域内加一个数字,每次询问一个矩形区域的和,则先考虑静态问题,即只询问,该问题可以用扫描线解决,考虑分治时,只用统计左边对右边的贡献,以左边所有插入为初始,只处理右边询问,这是一个静态问题,复杂度 \(O(nlogn)\),则总复杂度为 \(O(nlog^2n)\)
大部分情况下,动态问题在离线以后,会转化为每次询问时处理时间小于等于询问的贡献,这其实是时间上的一维偏序,用 cdq 可将这一维偏序处理掉
动态逆序对,考虑所有删除时间中 \(i< j\) ,\(a[i]>a[j]\),\(time_i<time_j\)或
\(i< j\) ,\(a[i]>a[j]\),\(time_i>time_j\) 的数对,他们对答案 \(time_i\) 和之前的询问有贡献,实际上就是三维偏序
点击查看代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<string>
#include<cstring>
using namespace std;
int n,m,inf=0x3f3f3f3f;
int dfn[6400100];
struct node{
int a,b,c;
}sol[2001000];
int ci[2000100],Max=1e6+5;
long long ans[2001000],cnt;
int lowbit(int x){return x&(-x);}
void add(int x,int k)
{
for(int i=x;i;i-=lowbit(i))
{
ci[i]+=k;
}
}
int ask(int x)
{
int sum=0;
for(int i=x;i<=Max;i+=lowbit(i))
{
sum+=ci[i];
}
return sum;
}
bool cmp1(node x,node y)
{
return x.a<y.a;
}
bool cmp2(node x,node y)
{
return x.c>y.c;
}
void cdq(int L,int R)
{
if(L==R) return ;
int mid=(L+R)>>1;
cdq(L,mid);cdq(mid+1,R);
sort(sol+L,sol+1+mid,cmp2);sort(sol+mid+1,sol+R+1,cmp2);
int l=L,r=mid+1;
for(int i=r;i<=R;i++)
{
while(l<=mid&&sol[l].c>sol[i].c)
{
add(min(sol[l].b,m),1);
l++;
}
ans[min(sol[i].b,m)]+=ask(min(sol[i].b,m));
}
for(int i=L;i<l;i++) add(min(sol[i].b,m),-1);
l=mid,r=R;
for(int i=l;i>=L;i--)
{
while(r>=mid+1&&sol[r].c<sol[i].c)
{
add(min(sol[r].b,m),1);
r--;
}
ans[min(sol[i].b,m)]+=ask(min(sol[i].b,m)+1);
}
for(int i=R;i>r;i--) add(min(sol[i].b,m),-1);
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>sol[i].c;sol[i].a=i;sol[i].b=inf;
dfn[sol[i].c]=i;
}
for(int i=1;i<=m;i++)
{
int x;
cin>>x;
sol[dfn[x]].b=i;
}
sort(sol+1,sol+1+n,cmp1);
cdq(1,n);
for(int i=m;i>=1;i--) ans[i]+=ans[i+1];
for(int i=1;i<=m;i++) cout<<ans[i]<<endl;
return 0;
}
整体二分
有的询问,套用二分可以用 \(O(nlogn)\) 的时间解决,但有时询问很多,会超时,这时使用整体二分即可在 \(O(nlog^2n)\) 解决
整体二分需满足以下条件(摘自《浅谈数据结构题几个非经典解法》)
-
询问的答案具有可二分性
-
修改对判定答案的贡献互相独立,修改之间互不影响效果
-
修改如果对判定答案有贡献,则贡献为一确定的与判定标准无关的值
-
贡献满足交换律,结合律,具有可加性
-
题目允许使用离线算法
该算法一般有一个 \(l\) 和 \(r\) ,为答案所在的域值,一个 \(L\) ,\(R\) 为只考虑之间的操作,首先二分一个答案 \(mid\) ,处理 \(L\) 到 \(R\) 之间的操作,找出所有询问与 \(mid\) 的关系,依据大小关系分成两组,分别进行递归,直到 \(l\) 与 \(r\) 相等,找到答案
给出一道经典例题
问题一: 给出一个数列,询问全局第 \(k\) 小数
这是一个可二分问题,不妨考虑二分答案是 \(mid\) ,只查询 小于等于 \(mid\) 的数的个数,这可以用树状数组解决
不难发现,该问题可直接扩展到单点修改
问题二: 询问区间第 \(k\) 小数
一种方法是可持久化线段树,这里不过多展开
另一种方法是整体二分,考虑这样的算法
对整体进行二分,得到一个答案 \(mid\) ,处理所有询问的在 \(l\) 到 \(mid\) 个数 ,若大于等于 \(k\) ,分到左边进行递归,若小于 \(k\) 则应分到右边进行递归
对于一个询问,在 \(l\) 到 \(mid\) 的区间有 \(cnt\) 个数,若大于等于 \(k\) ,等价于在左边查询第 \(k\) 小数,如果小于 \(k\) ,等价于在右边查询第 \(k-cnt\) 小数
点击查看代码
void solve(int l,int r,int L,int R)
{
if(l==r)
{
for(int i=L;i<=R;i++)
{
//如果是查询,则答案为l
}
return ;
}
int mid=(l+r)>>1,cnt1=0,cnt2=0;
for(int i=1;i<=n;i++)
{
if(a[i]<=mid) add(i,1);
}
for(int i=L;i<=R;i++)
{
int x=query(b[i].r)-query(b[i].l-1);
if(x>=k) q1[++cnt1]=b[i];
else b[i].k-=x,q2[++cnt1]=t[i];
}
for(int i=1;i<=n;i++)
{
if(a[i]<=mid) add(i,-1);
}
for(int i=1;i<=cnt1;i++)
{
b[L+i-1]=q1[i];
}
for(int i=1;i<=cnt2;i++)
{
b[L+cnt1+i-1]=q2[i];
}
solve(l,mid,L,L+cnt1-1);solve(mid+1,r,L+cnt1,R);
}
问题三 :单点修改,查询区间第 \(k\) 小数
一种方法是树套树,这里不过多展开
另一种方法还是整体二分,将修改查询一起处理,每个修改依据 \(mid\) 区分大小,同时按顺序处理询问
注意在分别递归时,左右仍要保持时间顺序大小不变
所以整体二分可直接扩展到修改
点击查看代码
void solve(int l,int r,int L,int R)
{
if(l==r)
{
for(int i=L;i<=R;i++)
{
//如果是查询,则答案为l
}
return ;
}
int mid=(l+r)>>1,cnt1=0,cnt2=0;
for(int i=L;i<=R;i++)
{
//如果是修改
if(b[i].v<=mid)
{
add(b[i].x,1);q1[++cnt1]=b[i];
}
else q2[++cnt2]=b[i];
//如果是查询
int x=query(b[i].r)-query(b[i].l-1);
if(x>=k) q1[++cnt1]=b[i];
else b[i].k-=x,q2[++cnt1]=t[i];
}
for(int i=1;i<=n;i++)
{
if(a[i]<=mid) add(i,-1);
}
for(int i=1;i<=cnt1;i++)
{
b[L+i-1]=q1[i];
}
for(int i=1;i<=cnt2;i++)
{
b[L+cnt1+i-1]=q2[i];
}
solve(l,mid,L,L+cnt1-1);solve(mid+1,r,L+cnt1,R);
}
板子题,只要将树状数组改成二维即可,不过多解释
点击查看代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
struct node{
int x,y,xi,yi,k,opt,rnk;
}t[650010],q1[650010],q2[650010];
int cnt;
long long n,q;
int a[5050][5005];
int tr[5050][5050];
int ans[650010],inf=1e9;
int lowbit(int x){return x&(-x);}
void add(int x,int y,int k)
{
for(;x<=n;x+=lowbit(x))
{
for(int j=y;j<=n;j+=lowbit(j))
{
tr[x][j]+=k;
}
}
}
int query(int x,int y)
{
if(!x||!y) return 0;
int ans=0;
for(;x;x-=lowbit(x))
{
for(int j=y;j;j-=lowbit(j))
{
ans+=tr[x][j];
}
}
return ans;
}
int ask(int x,int y,int xx,int yy)
{
return query(xx,yy)-query(x-1,yy)-query(xx,y-1)+query(x-1,y-1);
}
void sol(int l,int r,int L,int R)
{
if(L>R) return ;
if(l==r)
{
for(int i=L;i<=R;i++)
{
if(t[i].opt==1) ans[t[i].rnk]=l;
}
return ;
}
int mid=(l+r)>>1,cnt1=0,cnt2=0;
for(int i=L;i<=R;i++)
{
if(t[i].opt==0)
{
if(t[i].k<=mid)
{
q1[++cnt1]=t[i];add(t[i].x,t[i].y,1);
}
else q2[++cnt2]=t[i];
}
else
{
int sum=ask(t[i].x,t[i].y,t[i].xi,t[i].yi);
if(sum>=t[i].k) q1[++cnt1]=t[i];
else t[i].k-=sum,q2[++cnt2]=t[i];
}
}
for(int i=1;i<=cnt1;i++)
{
if(q1[i].opt==0) add(q1[i].x,q1[i].y,-1);
}
for(int i=L;i<=L+cnt1-1;i++)
{
t[i]=q1[i-L+1];
}
for(int i=L+cnt1;i<=R;i++)
{
t[i]=q2[i-L-cnt1+1];
}
sol(l,mid,L,L+cnt1-1);
sol(mid+1,r,L+cnt1,R);
}
int main()
{
cin>>n>>q;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cin>>a[i][j];
cnt++;t[cnt].opt=0;t[cnt].k=a[i][j];t[cnt].x=i;t[cnt].y=j;
}
}
for(int i=1;i<=q;i++)
{
cnt++;
cin>>t[cnt].x>>t[cnt].y>>t[cnt].xi>>t[cnt].yi>>t[cnt].k;
t[cnt].opt=1;t[cnt].rnk=i;
}
sol(0,inf,1,cnt);
for(int i=1;i<=q;i++) cout<<ans[i]<<endl;
return 0;
}
线段树分治
准确地说,这不应算一种分治,只是利用线段树的优秀性质(实际上分治和线段树对整体的划分是一致的,所以在某些问题上二者可以互相转化),可称之为线段树上进行原序列操作
它可以处理这样的问题
已知一数据结构插入复杂度是 \(O(T(n))\) 的,现加入删除操作,则利用线段树分治可在 \(O(T(n)\log n)\) 的时间内处理删除
考虑每次插入后,插入到删除之间的时间构成了该次插入在数据结构上的存活时间,则该存活时间之内他会造成影响,考虑对时间建一棵线段树,则该存活时间会被拆成 \(\log n\) 个节点,在这些节点保存下该次插入,最后遍历整个线段树,每遍历到一个节点,执行该节点保存的所有插入,在向下递归,到叶子时处理询问,回溯时按顺序撤回所有插入,这样就完成了删除
可以发现,线段树分治只针对删除且需要离线,是一种强大的工具,但前提是插入,撤回,询问有优秀的做法,不然便不能适用
动态加边,动态删边,判断是否为二分图
先考虑动态加边,可以用拓展域并查集维护
删边只需用线段树分治,注意并查集要支持撤销,不能写路径压缩,应写按秩合并
点击查看代码
```#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
struct node{
int u,v;
}a[6400100];
struct merge_set{
int fa,siz;
}f[6400100];
struct tree{
int l,r;
vector<int>now;
}t[6400100];
int ans[640010];
pair<int,int>sta[6400100];
int top;
int n,m,k;
void init(int all)
{
for(int i=1;i<=all;i++)
{
f[i].fa=i;f[i].siz=1;
}
}
int find(int x){return x==f[x].fa?x:find(f[x].fa);}
void merge(int x,int y)
{
x=find(x);y=find(y);
if(f[y].siz>f[x].siz) swap(x,y);
sta[++top]={y,f[y].fa};
f[y].fa=x;f[x].siz+=f[y].siz;
}
void del()
{
int y=sta[top].first,x=f[y].fa;
f[x].siz-=f[y].siz;f[y].fa=sta[top].second;
top--;
}
void build(int p,int L,int R)
{
// cout<<p<<" "<<L<<" "<<R<<endl;
t[p].l=L;t[p].r=R;
if(L==R) return ;
int mid=(L+R)>>1;
build(p*2,L,mid);build(p*2+1,mid+1,R);
}
void change(int p,int L,int R,int x)
{
if(L<=t[p].l&&t[p].r<=R)
{
// cout<<p<<" "<<x<<endl;
t[p].now.push_back(x);
return ;
}
int mid=(t[p].l+t[p].r)>>1;
if(L<=mid) change(p*2,L,R,x);
if(mid+1<=R) change(p*2+1,L,R,x);
}
void tree_del(int stk,int lak)
{
for(int i=stk;i<=lak;i++) del();
}
void solve(int p)
{
int stk=top+1,lak;
for(int i=0;i<t[p].now.size();i++)
{
int x=t[p].now[i];
int u=find(a[x].u),v=find(a[x].v);
if(find(a[x].u)==find(a[x].v))
{
for(int j=t[p].l;j<=t[p].r;j++)
{
ans[j]=-1;
}
lak=top;
tree_del(stk,lak);
return ;
}
// if(u>n) u-=n;
// if(v>n) v-=n;
merge(a[x].u,a[x].v+n);merge(a[x].v,a[x].u+n);
}
lak=top;
if(t[p].l==t[p].r) ans[t[p].l]=1;
if(t[p].l!=t[p].r)
{
solve(p*2);solve(p*2+1);
}
tree_del(stk,lak);
}
int main()
{
cin>>n>>m>>k;
init(3*n);build(1,1,k);
for(int i=1;i<=m;i++)
{
int le,ri;
cin>>a[i].u>>a[i].v>>le>>ri;
if(le<ri) change(1,le+1,ri,i);
}
solve(1);
for(int i=1;i<=k;i++)
{
if(ans[i]==1) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
// cout<<ans[i]<<endl;
}
return 0;
}
</details>


 浙公网安备 33010602011771号
浙公网安备 33010602011771号