斜率优化dp
例题一
给你一些平面上的点,让你求凸包
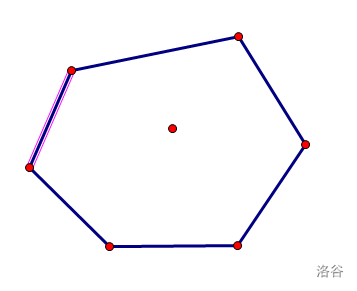
模板题不解释
如果只维护下面的凸包(称它为下凸壳)呢
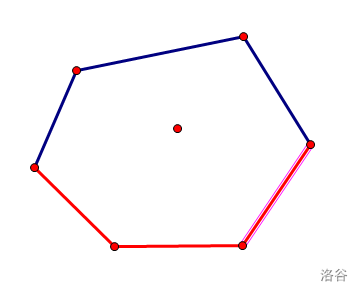
还是板子
如果按一定顺序给出且每加入一个点就输出当前的下凸包呢
动态凸包?
简化一下,按横坐标顺序给出点呢?
还用动态凸包就太麻烦了,不妨看一看有什么别的方法
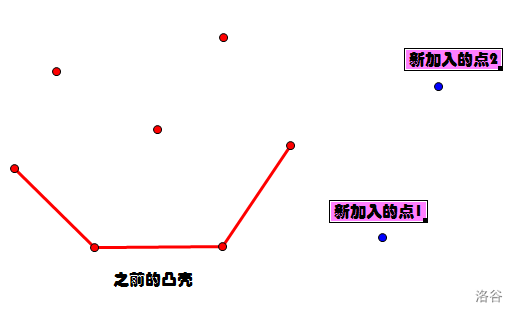
可以发现一条性质
之前不再凸壳的点之后也不会加入,新的凸壳要么是
之前的,要么是之前的与新加入的点形成的凸壳
这启示我们使用单调队列
如何维护呢
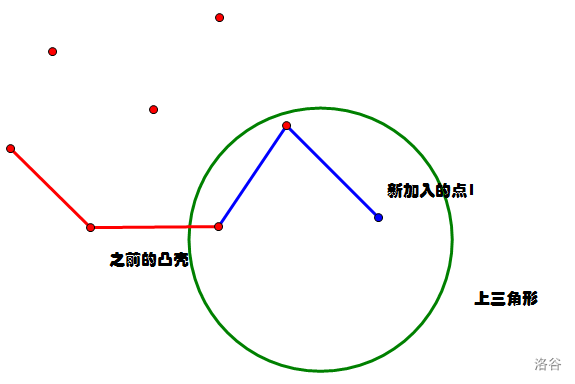
先看这种
可以发现上面的点是无用的,此时后三个点形成了上三角的形状,上三角形状有一个性质,前一条直线斜率大于与后一条直线斜率,可以 \(O(1)\) 判断是否为上三角
还有这种
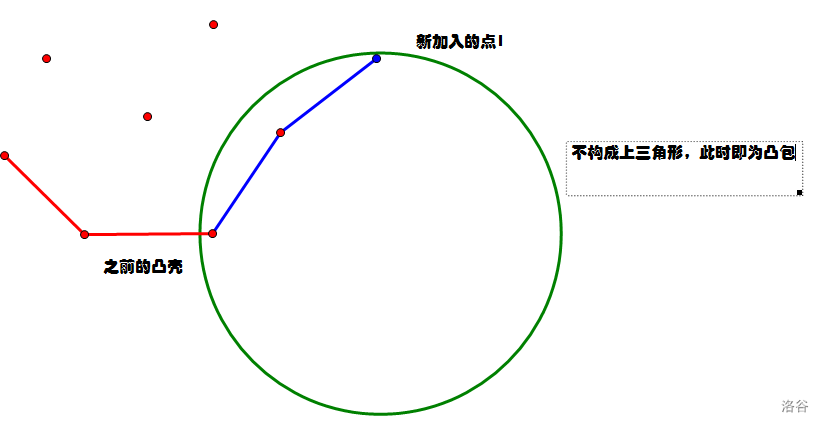
不构成上三角,此时就是新凸包。
还有一种
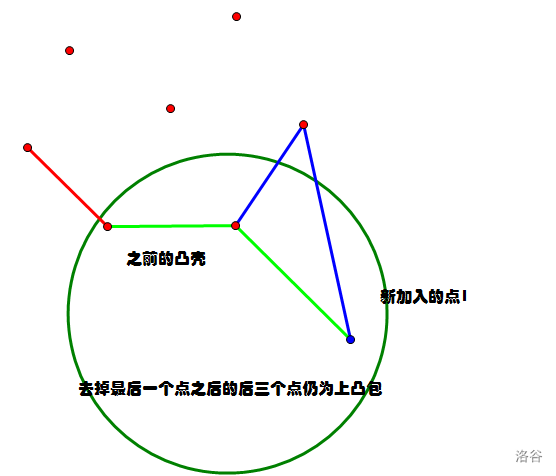
不仅最后一个点无用,倒数第二个也无用
可以总结出一种算法
使用单调队列维护凸包,每插入一个点之后,判断与前面的点是否构成上三角形,如果是,删除三角形顶点,如果不是,加入当前点后即为凸包
for(int i=1;i<=n;i++)
while(l<r&&slope(r-1,r)>slope(r,i)) r--;
//q为单调队列,r-1,r为单调队列最后两个点,i为新插入的点
r++;q[r]=i;
}
如果不按顺序呢
就用动态凸包吧,跟上面想法类似,用平衡树维护
先插入点,分别向左右两边执行上面的方法即可
void Insert(int x,int y)
{
if(s.size()<2) s.insert({x,y});//不足2个直接插入
set<pair<int,int> >::iterator nxt=s.lower_bound({x,y}),pre=s.lower_bound({x,y}),i;
pre--;
if(slope(pre->first,pre->second,x,y)>slope(nxt->first,nxt->second,x,y)) return ;//当前点不在凸包
i=--pre;
while(i!=s.begin()&&slope(i->first,i->second,pre->first,pre->second)>slope(pre->first,pre->second,x,y))//向前更新,要最开始先插入一个点为边界
{
s.erase(pre);pre=it;it--;
}
i=++nxt;
while(i!=s.end()&&slope(nxt->first,nxt->second,x,y)>slope(i->first,i->second,nxt->first,nxt->second))//向后更新
{
s.erase(nxt);nxt=it;it++;
}
s.insert({x,y});
}
例题2
给你一些平面上的点,每次加入点后都给出一条定斜率的直线,你需要找到过至少一个点的直线的最小截距
首先可以发现直线过的点一定在下凸壳上
先简化一下,直线斜率递增
不妨来看两个点
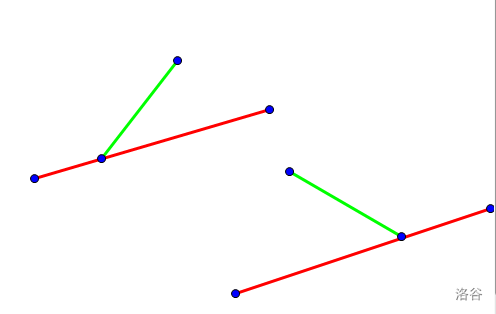
绿线为线段,红线为直线
发现一个性质,当线段斜率小于直线斜率时,前一个点一定不会是答案线段所在
又因为直线斜率递增,所以当线段斜率小于直线斜率时,前一个点在之后也一定不会是答案直线所在,满足单调性
再看一个凸包
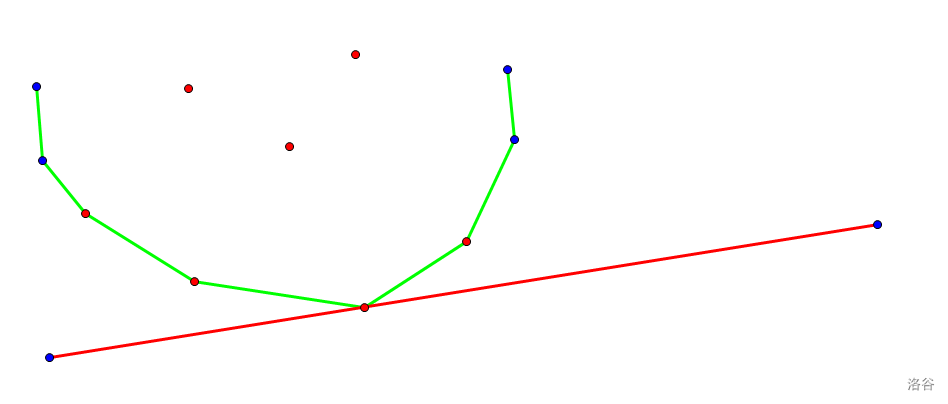
根据刚刚的结论,前面的点都是无用的,可以删去
于是便有了做法
若为单调队列,在队头判断线段斜率是否小于直线斜率,小于就删除,这样第一个点一定是答案直线所在。
for(int i=1;i<=n;i++)
{
while(l<r&&slope(l,l+1)<k) l++;//k为直线斜率
//这里输出答案
while(l<r&&slope(r-1,r)>slope(r,i)) r--;
//q为单调队列,r-1,r为单调队列最后两个点,i为新插入的点
r++;q[r]=i;
}
如果不递增呢
依照上面的图形,答案直线所在的点恰是前面斜率小于且后面斜率大于等于的点,这个点是可以二分的
如果是平衡树可以再开一个平衡树存两点间斜率,在这上面二分即可
以队列的为例
void check(int k)
{
if(l==r) return q[l];
int L=l,R=r,ans;
while(l<=r)
{
int mid=(l+r)>>1;
if(slope(mid,mid+1)>=k) ans=mid,r=mid-1;
else l=mid+1;
}
return q[ans];
}
以上,便是斜率优化的基本操作(明明是计算几何)
也就是说斜率优化dp都可以抽象成例题二的形式
如何转化呢?
不妨看一个式子
先把 \(\min\) 去掉并拆开平方
将包含 \(i\) 项的移至左侧,只包含 \(j\) 项的移至右侧
将乘积项中 \(a[j]\) 看成 \(x\) ,乘积项中 \(a[i]\) 看成 \(k\) ,只包含 \(j\) 项 看成 \(y\),只包含 \(i\) 项 看成 \(b\)
发现要求 \(f[i]\) 即是使 \(b\) 最大,且 \((x,y)\)只与 \(j\) 有关(即已知),\(k\) 只与 \(i\) 有关(即每次给出),这不就是例题二的形式吗?
若为 \(\max\) ,即维护上凸壳且找截距最大值
总结
做题方法
-
列出状态转移方程,且方程有与 \(i,j\) 有关的乘积项。
-
拆开式子,去 \(min\) 或 \(max\) ,包含 \(i\) 项的移至左侧,只包含 \(j\) 项的移至右侧,找出 \(k,x,y,b\)(方法同例子)
-
判断 \(k\) 是否单调决定用二分还是队列,判断 \(x\) 是否单调决定用队列还是平衡树,看是上凸壳还是下凸壳
-
直接套用即可
求斜率有精度丢失,一般用 long double,或者将 \((y[i]-y[j])/(x[i]-x[j])\leq k\) 化为 \((y[i]-y[j])\leq k*(x[i]-x[j])\) , 但一定要注意需不需变号
一般出题人都会让 \(k,x\) 单调,不排除有出 k , x 都不单调还在树上的出题人
枚举最后一只特别行动队的位置,不难推出方程,令 \(f[i]\) 为前 \(i\) 个士兵的最大修正战斗力,\(s[i]\) 为前 \(i\) 个士兵的战斗力前缀和
最后为
令 \(k\) 为 \(2\ast a\ast s[i]+b\) , \(x\) 为 \(s[j]\) , \(y\) 为 \(f[j]+a\ast s[j]^2+c\),发现 \(k\) 单调, \(x\) 单调,直接用单调队列
long long a,b,c;
int n,l=1,r=1;
int sum[1400100];
int q[6400100];
long long f[1001000];
long long y(int i) {return a*sum[i]*sum[i]+f[i]+c;}
long long x(int i) {return sum[i];}
int check(long long k)
{
while(l<r&&(y(q[l])-y(q[l+1]))<=k*(x(q[l])-x(q[l+1]))) l++;
return q[l];
}
int main()
{
memset(f,0xc0,sizeof(f));//极小值
cin>>n;
cin>>a>>b>>c;
for(int i=1;i<=n;i++)
{
int x;cin>>x;
sum[i]=sum[i-1]+x;
}
q[l]=0;f[0]=0;//队列初始一般有一个零点
for(int i=1;i<=n;i++)
{
int k=check(1ll*2*a*sum[i]+b);
f[i]=f[k]+1ll*a*(sum[i]-sum[k])*(sum[i]-sum[k])+b*(sum[i]-sum[k])+c;
while(l<r&&(y(q[r])-y(q[r-1]))*(x(i)-x(q[r]))<=(y(i)-y(q[r]))*(x(q[r])-x(q[r-1]))) r--;
r++;q[r]=i;
}
cout<<f[n];
return 0;
}
基本没有什么好的转移方式,只能考虑边到边的的转移
令 \(f[i]\) 为走完第 \(i\) 条边后的最小烦躁值,考虑枚举上一条边是什么,有方程
一眼斜率优化
现在有两个限制无法满足
- \(x_i=y_j\)
也就是在扫到 \(i\) 时,能快速找到符合条件的所有的 \(j\)
直接对每个点都开一个队列,将每个 \(i\) 更新完后插入 \(x_i\) 的队列中,每次查这个队列即可
2.\(p_i\geq q_j\)
也就是在扫到 \(i\) 时,所有符合条件的 \(j\) 都被算过
一种思路,按 \(p_i\) 从小到大排序(为什么不按 \(q_i\) ?),能保证之前所有符合条件的 \(j\) 都被算过
但会带来一个问题,作为横坐标的 \(q_j\) 不单调了,但又不想写平衡树
考虑这样一种思路,每次现将算完的 \(j\) 插入对应的优先队列当中(从小到大),每次查询时若有在优先队列中且符合条件的先插入队列在查询,因为队列插入有单调性,后插入的一定横坐标更大
代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
long long a,b,c;
struct node{
long long x,y,p,q;
}trai[1001000];
long long f[1001000];
long double eps=1e-9;
long long xi(int i)
{
return trai[i].q;
}
long long yi(int i)
{
return f[i]+trai[i].q*trai[i].q*a+c;
}
bool cmp(node i,node j)
{
return i.p<j.p;
}
long double slope(int i,int j)
{
long double up=yi(i)-yi(j),dow=xi(i)-xi(j);
return dow?(long double)(up/dow):(up>0?1e18:-1e18);//横坐标会相等,优先返回小的
}
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >s[200100];
deque<int>v[101000];
long long ans=1ll<<60;
void inser(int now,int x)
{
while(v[now].size()>1)
{
int las=v[now].back();v[now].pop_back();
int pre=v[now].back();
if(slope(las,pre)-slope(las,x)>eps) continue;
else
{
v[now].push_back(las);break;
}
}
v[now].push_back(x);
}
int check(int now,long long pos)
{
while(!s[now].empty())
{
if(s[now].top().first<=pos) inser(now,s[now].top().second),s[now].pop();
else break;
}
if(v[now].empty()) return -1;
while(v[now].size()>1)
{
int pre=v[now].front();v[now].pop_front();
int las=v[now].front();
if(slope(pre,las)-(long double)(2.0*a*pos+b*1.0)<eps) continue;
else
{
v[now].push_front(pre);break;
}
}
return v[now].front();
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int main()
{
memset(f,0x3f,sizeof(f));
n=read();m=read();a=read();b=read();c=read();
for(int i=1;i<=m;i++)
{
trai[i].x=read();trai[i].y=read();trai[i].p=read();trai[i].q=read();
}
sort(trai+1,trai+1+m,cmp);
v[1].push_back(0);f[0]=0;
for(int i=1;i<=m;i++)
{
int k=check(trai[i].x,trai[i].p);
if(k!=-1)
{
f[i]=f[k]+a*(trai[i].p-trai[k].q)*(trai[i].p-trai[k].q)+b*(trai[i].p-trai[k].q)+c;
s[trai[i].y].push({trai[i].q,i});
}
if(trai[i].y==n)
{
ans=min(ans,f[i]+trai[i].q);
}
}
cout<<ans;
return 0;
}
由于本题非常好,且属于斜率优化的毕业题,所以讲一下
分数据点考虑
t=0
没有距离限制,且是一条链
每个节点只能跳到祖先节点,再从祖先节点跳到终点,显然节点跳到祖先节点是一次决策,考虑令 \(dp[i]\) 为从根节点到该节点的最小资金,有
\(dp[i]=\min(dp[j]+p[i]\ast (dis[i]-dis[j])+q[i])\) ,其中 \(j\) 为 \(i\) 的祖先
考虑斜率优化,有
注意, \(p[i]\) 并不单调,需要二分查询交点
t=2
有距离限制
能跳到的最远的节点显然可以预处理出来,用树上倍增处理
for(int i=2;i<=n;i++)
{
int k=i;
for(int j=20;j>=0;j--)
{
if(f[k][j]!=0&&dis[i]-dis[f[k][j]]<=l[i])
{
k=f[k][j]//f是倍增数组
}
}
up[i]=dep[k];//up是上界节点
}
考虑一个凸包,如果只在当前凸包上找到所有能转移的点转移是不可以的
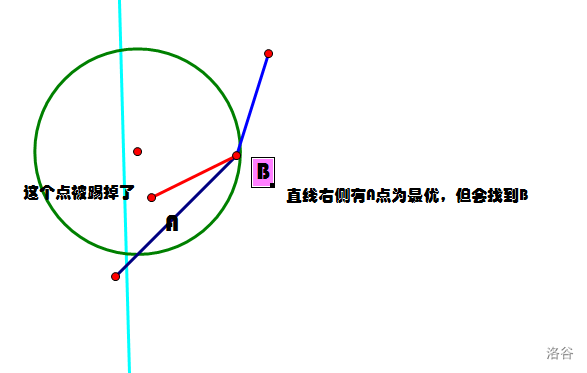
考虑一点,如果这个区间能表示成若干个已知的区间,只要查询这些区间既可以了
本题每次的区间一定是后缀区间,考虑使用树状数组套单调栈,树状数组的节点维护从当前到结尾的
单调栈,每次查询后缀 \(\min\) ,加入节点时将每一个对应栈都加入一个数
int lowbit(int x){return x&(-x);}
void add(int x,int now)
{
for(;x<=n;x+=lowbit(x))
{
pus(t[x].dfn,now);
}
}
ll query(int x,int now)
{
ll minn=1ll<<62;
for(;x;x-=lowbit(x))
{
minn=min(minn,quer(t[x].dfn,now));
}
return minn;
}
void dfs_sol(int now,int fath)
{
if(now!=1) dp[now]=query(n-max(up[now],1ll)+1,now);
//基本的树状数组只能维护前缀和,考虑翻转序列就可查询后缀
add(n-dep[now]+1,now,1);
for(int i=head[now];i;i=e[i].next)
{
int v=e[i].to;
if(v!=fath)
{
dfs_sol(v,now);
}
}
add(n-dep[now]+1,now,-1);
t=3
是一棵树
考虑每次从遍历完子节点后,需要删去该节点再在之后更新别的节点,也就是说,单调栈是可撤销的
考虑维护可撤销单调栈
考虑每次操作,先找到应该插入的位置,将插入前该位置的值和栈顶记录下来,之后直接将插入的位置替换为该位置,撤销时直接换回去就行了
void pus(int now,int i)
{
int pre=sum[now];
while(sum[now]>=2)
{
node pre1=ai[q[now][sum[now]-1]],pre2=ai[q[now][sum[now]]];
if(slope(pre1.toi,pre2.toi)>slope(pre2.toi,i))
{
sum[now]--;
}
else break;
}
sum[now]++;scnt++;
while(q[now].size()<sum[now]+1) q[now].push_back(0);
ai[scnt]={i,q[now][sum[now]],pre};
q[now][sum[now]]=scnt;
}
void los(int now)
{
int tt=q[now][sum[now]];
q[now][sum[now]]=ai[tt].las;
sum[now]=ai[tt].su;
}
完整代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<queue>
#include<stack>
#include<vector>
#define ll long long
using namespace std;
struct node{
int toi,las,su;
};
struct edge{
int to,next;
ll cost;
}e[500100];
int head[200100],cnt;
void addi(int u,int v,ll w)
{
e[++cnt]={v,head[u],w};
head[u]=cnt;
}
long double eps=1e-9;
vector<int>q[800100];
struct tree{
int dfn;
}t[800100];
int n,tr,lcnt,scnt,ccnt,rt;
ll p[200100],qi[200100],l[200100],up[200100];
int f[200100][22],dep[200100];
ll dis[200100];
ll dp[200100];
int sum[200100];
node ai[9400100];
long double slope(int x,int y)
{
ll u1=dp[x]-dp[y],d1=dis[x]-dis[y];
return 1.0*u1/d1;
}
void pus(int now,int i)
{
int pre=sum[now];
while(sum[now]>=2)
{
node pre1=ai[q[now][sum[now]-1]],pre2=ai[q[now][sum[now]]];
if(slope(pre1.toi,pre2.toi)>slope(pre2.toi,i))
{
sum[now]--;
}
else break;
}
sum[now]++;scnt++;
while(q[now].size()<sum[now]+1) q[now].push_back(0);
ai[scnt]={i,q[now][sum[now]],pre};
q[now][sum[now]]=scnt;
}
void los(int now)
{
int tt=q[now][sum[now]];
q[now][sum[now]]=ai[tt].las;
sum[now]=ai[tt].su;
}
ll quer(int now,int i)
{
int L=1,R=sum[now];
if(L>R) return 1ll<<62;
if(L==R)
{
int k=ai[q[now][sum[now]]].toi;
return dp[k]+p[i]*(dis[i]-dis[k])+qi[i];
}
while(L<R)
{
int mid=(L+R)>>1;
node pre1=ai[q[now][mid]],pre2=ai[q[now][mid+1]];
if(slope(pre1.toi,pre2.toi)<=1.0*p[i]) L=mid+1;
else R=mid;
}
int k=ai[q[now][L]].toi;
return dp[k]+p[i]*(dis[i]-dis[k])+qi[i];
}
int lowbit(int x){return x&(-x);}
void add(int x,int now,int op)
{
for(;x<=n;x+=lowbit(x))
{
if(op==1) pus(t[x].dfn,now);
else los(t[x].dfn);
}
}
ll query(int x,int now)
{
ll minn=1ll<<62;
for(;x;x-=lowbit(x))
{
minn=min(minn,quer(t[x].dfn,now));
}
return minn;
}
void dfs_pre(int now,int fath)
{
f[now][0]=fath;dep[now]=dep[fath]+1;
for(int i=1;i<=20;i++)
{
f[now][i]=f[f[now][i-1]][i-1];
}
for(int i=head[now];i;i=e[i].next)
{
int v=e[i].to;
if(v!=fath)
{
dis[v]=dis[now]+e[i].cost;
dfs_pre(v,now);
}
}
}
void dfs_sol(int now,int fath)
{
if(now!=1) dp[now]=query(n-max(up[now],1ll)+1,now);
add(n-dep[now]+1,now,1);
for(int i=head[now];i;i=e[i].next)
{
int v=e[i].to;
if(v!=fath)
{
dfs_sol(v,now);
}
}
add(n-dep[now]+1,now,-1);
}
signed main()
{
// freopen("txt.in","r",stdin);
// freopen("txt.out","w",stdout);
cin>>n>>tr;
for(int i=1;i<=n;i++)
{
t[i].dfn=++lcnt;
}
for(int i=2;i<=n;i++)
{
ll s,fa;
cin>>fa>>s>>p[i]>>qi[i]>>l[i];
addi(i,fa,s);addi(fa,i,s);
}
dfs_pre(1,0);
for(int i=2;i<=n;i++)
{
int k=i;
for(int j=20;j>=0;j--)
{
if(f[k][j]!=0&&dis[i]-dis[f[k][j]]<=l[i])
{
k=f[k][j];
}
}
up[i]=dep[k];
}
dfs_sol(1,0);
for(int i=2;i<=n;i++)
{
cout<<dp[i]<<endl;
}
// fclose(stdin);fclose(stdout);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号