清北刷题10.23night

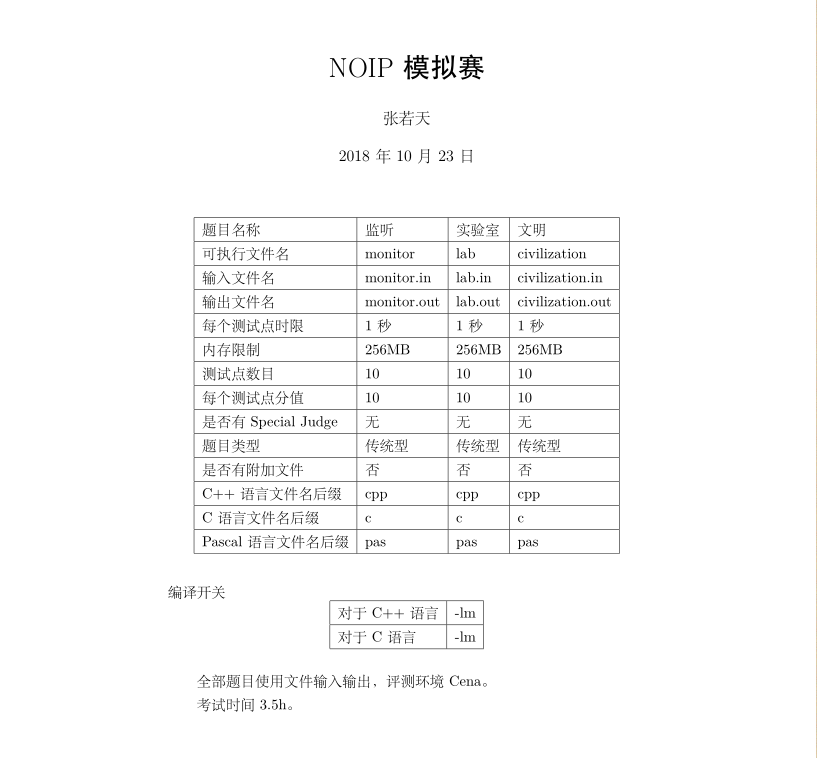
NOIP 模拟赛
张若天
2018 年 10 ⽉ 23 ⽇
题⽬名称 监听 实验室 ⽂明
可执⾏⽂件名 monitor lab civilization
输⼊⽂件名 monitor.in lab.in civilization.in
输出⽂件名 monitor.out lab.out civilization.out
每个测试点时限 1 秒 1 秒 1 秒
内存限制 256MB 256MB 256MB
测试点数⽬ 10 10 10
每个测试点分值 10 10 10
是否有 Special Judge ⽆ ⽆ ⽆
题⽬类型 传统型 传统型 传统型
是否有附加⽂件 否 否 否
C++ 语⾔⽂件名后缀 cpp cpp cpp
C 语⾔⽂件名后缀 c c c
Pascal 语⾔⽂件名后缀 pas pas pas
编译开关
对于 C++ 语⾔ -lm
对于 C 语⾔ -lm
全部题⽬使⽤⽂件输⼊输出，评测环境 Cena。
考试时间 3.5h。
忘了什么时候开始
到清晨才能⼊睡
也忘了什么叫做结尾
又有谁在乎呢
凌晨三点的窗前
播放着那段时光
有⼀个骄傲的少年
隐藏他的青春
— 张希/曹⽅《认真地老去》
2
监听
monitor.in/.out/.cpp
弱小和⽆知不是⽣存的障碍，拖延症才是。
【背景】
不阅读本题的【背景】并不影响通过本题。
三体信息中没有包含对三体⼈⽣物形态的任何描述，⼈类要在四百多年
以后才能真正看到三体⼈。在阅读信息时，叶⽂洁只能把三体⼈想象成⼈类
的形象。
1379 号监听站已经存在了上千年，像这样的监听站，在三体世界中有
⼏千个，它们全神贯注地聆听着宇宙间可能存在的智慧⽂明的信息。
最初监听站中有上百名监听员，但随着技术的进步，现在只有⼀个⼈值
守了。监听员是⼀个卑微的职业，他们虽然⾝处恒温且能保证⽣活供给的监
听室中，在乱世纪不必脱⽔，但他们的⽣命也就在这⼩⼩的空间中流逝，能
够享受到的恒纪元快乐⽐其他⼈要少得多。
1379 号监听员投过⼩⼩的床⼦看着外⾯的三体世界，这是乱纪元的⿊
夜，巨⽉还没有升起来，⼤多数⼈都处于脱⽔的冬眠中，甚⾄植物也本能地
脱⽔了，成了附着于地表没有⽣命的⼀束⼲纤维。星光下，⼤地看上去像⼀
⼤块冰冷的⾦属。
这是最孤寂的时刻，在静静的午夜，宇宙向它的聆听者展⽰着⼴漠的荒
凉。1379 号监听员最不愿意看的，就是显⽰器上缓缓移动的那条曲线，那是
监听系统接收到的宇宙电波的波形，⽆意义的噪声。他感到这条⽆限长的线
就是宇宙的抽象，⼀头连着⽆限的过去，另⼀头连着⽆限的未来，中间只有
为⽆规律⽆⽣命的随机起伏。⼀个个⾼低错落的波峰就像⼀粒粒⼤⼩不等的
沙⼦，整条线就像是所有沙粒排成⾏形成的⼀维沙漠，荒凉寂寥，长得令⼈
⽆法忍受。你可以沿着它向前向后⾛⽆限远，但永远找不到归宿。
【问题描述】
监听的宇宙电波可以抽象成⼀个长度为 L 的⼩写字母组成的字符串。
3
同时在三体⼈总结出来了 n 段敏感电波的样⼦，每段敏感电波的长度
都是 m。
现在请你实现⼀个程序，求出在这长度为 L 的⼩写字母组成的字符串
中某个敏感电波第⼀次出现的位置（位置从 1 开始计数） 。
如果从头到尾，没有任何敏感电波出现，输出”no”（不带双引号） 。
【输入格式】
第⼀⾏三个整数 L, n, m。
接下来 n ⾏，每⾏⼀个长度为 m 的字符串，表⽰敏感电波。
接下来⼀⾏，⼀个长度为 L 的字符串，表⽰监听到的电波。
【输出格式】
输出⼀个整数或者⼀个字符串”no”（不带双引号） 。
【样例输入 1】
11 3 3
aba
cba
abc
aaabbabcaba
【样例输出 1】
6
【样例输入 2】
11 3 3
aba
cba
abc
4
aaabbabzabz
【样例输出 2】
no
【数据规模及约定】
对于前 30% 的数据，1 ≤ L ≤ 100, 1 ≤ n ≤ 100, 1 ≤ m ≤ 20。
对于前 50% 的数据，1 ≤ L ≤ 10000, 1 ≤ n ≤ 1000, 1 ≤ m ≤ 20。
对于另外 20% 的数据，n = 1。
对于前 100% 的数据，1 ≤ L ≤ 10 5 , 1 ≤ n ≤ 10 4 , 1 ≤ m ≤ 20。
5
实验室
lab.in/.out/.cpp
光锥之内都是新闻。
【背景】
不阅读本题的【背景】并不影响通过本题。
《时间之外的往事》(节选) 弯曲空间的动⼒
这个宇宙的空间并不是平坦的，⽽是存在着曲率，如果把宇宙的整体想
象为⼀张⼤膜，这张膜的表⾯是弧形的，整张膜甚⾄可能是⼀个封闭的肥皂
泡。虽然膜的局部看似平⾯，但空间曲率还是⽆处不在。
早在公元世纪，曾出现过许多极富野⼼的宇宙航⾏设想，其中之⼀就是
空间折叠。设想把⼤范围空间的曲率⽆限增⼤，像⼀张纸⼀样对折，把“纸
⾯”上相距千万光年的遥远的两点贴在⼀起。这个⽅案严格说来不应称为宇
宙航⾏，⽽应该叫做。 “宇宙拖曳” ，因为它实质上并不是航⾏到⽬的地，⽽是
通过改变空间曲率把⽬的地花过来。
这种⽓吞宇宙的事只有上帝才做得⼭来. 如果加上基本理论的限制.
可能上帝也不⾏。
对于利⽤空间曲率航⾏，后来又出现了⼀个更温和更局部的设想，⼀艘
处于太空中的飞船，如果能够⽤某种⽅式把它后⽽的⼀部分空间熨平，减⼩
其曲率、那么飞船就会被前⽅曲率史⼤的空间拉过去，这就是曲率驱动。
曲率驱动不可能像空间折叠那样瞬间到达⽬的地，但却有可能使飞船以
⽆限接近光速的速度航⾏。
但直到云天明情报被正确解读前，曲率驱动仍是⼀个幻想，同上百个光
速飞⾏的幻想⽅案⼀样， ⽆论从理论上还是技术上， 没有⼈知道它是否可⾏。
【问题描述】
沿着着曲率驱动的思路，R 君开发出了时间旅⾏传送门。
R 君将 n-1 个时间旅⾏传送门部署到了 n 个星球。如果只⾛这 n-1 个
时间旅⾏传送门，R 君发现这 n 个星球是两两可达的（也就是⼀棵树） 。
6
但是时间旅⾏传送门除了传送的功能外还额外有着时间旅⾏的功能，⽐
如说 (X i , Y i , T i ) 这个传送门，通过这个传送门从 X i 到 Y i 时间就会增加
T i (T i 可正可负)，通过这个传送门从 Y i 到 X i 时间就会减少 T i (T i 可正可
负)。
现在 R 君关⼼的问题是从 x 星球能不能通往 y 星球，同时时间恰好增
加 z（z 可正可负） 。
由于现在是⼀个树形的结构，所以实际上两点之间的路径唯⼀，所以 R
君很快写了个程序计算出了这个结果。
但是随着 R 君继续部署传送门，这个问题变得复杂了起来，所以请你
来帮帮忙。
【输入格式】
第⼀⾏两个整数 n，q。q 表⽰之后处理的事件的数量。
接下来 n-1 ⾏，每⾏三个整数 x i ,y i ,T i 。
接下来 q ⾏，每⾏四个正整数 k, x, y, t。
若 k=0，表⽰部署⼀个新的传送门 (x,y,t)。
若 k=1，表⽰询问是否可以从 x 到 y，使得时间恰好增加 t。
【输出格式】
对于每个 k=1 的询问，输出⼀⾏⼀个答案 yes/no。 （⼩写）
【样例输入】
5 5
1 2 1
2 3 1
3 4 1
4 5 2
1 1 5 5
1 2 5 5
1 1 5 10
7
0 2 4 -3
1 1 5 10
【样例输出】
yes
no
no
yes
【样例解释】
添加 (2,4,-3) 后可以从 1->2->3->4->2->3->4->5， 时间变化是 1+1+1-
(-3)+1+1+2=10。
【数据规模及约定】
对于前 30% 的数据，1 ≤ n ≤ 1000, 1 ≤ q ≤ 1000 , |T i | ≤ 10 9 。
对于另外 20% 的数据，不存在 k=0 的输⼊。
对于另外 20% 的数据，只存在⼀条 k=0 的输⼊。
对于前 100% 的数据，1 ≤ n ≤ 10 5 , 1 ≤ q ≤ 4 × 10 5 , |T i | ≤ 10 9 。
8
文明
civilization.in/.out/.cpp
给岁月以⽂明，⽽不是给⽂明以岁月。
【背景】
不阅读本题的【背景】并不影响通过本题。
罗辑那边的⽕星升了起来并来回移动，显然是他站起⾝来踱步，在地球
上是可以的，但在宇宙中不⾏，下⾯我们引⼊⼀个重要概念：猜疑链。挺怪
的词⼉。我开始仅得到这么⼀个词，她没有解释，但我后来终于从字⾯上推
测出了它的含义。他？他是谁？后⾯再说吧，我们继续：如果你认为我是善
意的，这并不是你感到安全的理由，因为按照第⼀条公理，善意⽂明并不能
预先把别的⽂明也想成善意的，所以，你现在还不知道我是怎么认为你的，
你不知道我认为你是善意还是恶意；进⼀步，即使你知道我把你也想象成善
意的，我也知道你把我想象成善意的，但是我不知道你是怎么想我怎么想你
怎么想我的，挺绕的是不是？这才是第三层，这个逻辑可以⼀直向前延伸，
没完没了。我懂你的意思。这就是猜疑链。这种东西在地球上是见不到的。
⼈类共同的物种、相近的⽂化、同处⼀个相互依存的⽣态圈、近在咫尺的距
离，在这样的环境下，猜疑链只能延伸⼀⾄两层就会被交流所消解。但在太
空中，猜疑链则可能延伸得很长，在被交流所消解之前，⿊暗战役那样的事
已经发⽣了。
【问题描述】
R 君在继续着宇宙社会学的研究，R 君发现是否为善意的⽂明与他们的
距离到本⽂明的距离的奇偶有很⼤的关系。
所以 R 君提出了如下简化的问题，考虑⼀个 n 个节点带边权的树，两
点间距离是两点间树上路径的边权和。
R 君想知道对于⼀个点来说，到这个点是距离奇数的节点的距离和，与
到这个点距离是偶数的节点的距离和。
9
【输入格式】
第⼀⾏包含两个整数 n, q。q 表⽰询问数量。
接下来 n-1 ⾏，每⾏三个数字 (x,y,z) 表⽰ x 与 y 之间的距离是 z。
接下来 q ⾏，每⾏⼀个整数 x，表⽰询问的节点为 x。
【输出格式】
输出包含 q ⾏，每⾏两个整数，分别表⽰距离为奇数的节点的距离和与
距离为偶数的节点的距离和。
【样例输入】
4 4
1 2 1
2 3 2
2 4 3
1
2
3
4
【样例输出】
4 4
4 2
8 2
8 4
【样例解释】
每个点到 1 号点的距离：0,1,3,4
每个点到 2 号点的距离：1,0,2,3
每个点到 3 号点的距离：3,2,0,5
10
每个点到 4 号点的距离：4,3,5,0
【数据规模和约定】
对于前 20% 的数据，1 ≤ n ≤ 100。
对于前 40% 的数据，1 ≤ n ≤ 2000。
对于前 70% 的数据，1 ≤ n ≤ 5 × 10 4 。
对于前 100% 的数据，1 ≤ n ≤ 10 5 , q ≤ n, 1 ≤ z ≤ 10 3 。
11
（完）
12

 

/*
string + map 水过
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<map>

#define N 100007

using namespace std;
int n,m,l,ans,cnt;
string s[10002];
map<string,bool>vis;
string ss;

int main()
{
    freopen("monitor.in","r",stdin);
    freopen("monitor.out","w",stdout);
    scanf("%d%d%d",&l,&n,&m);
    for(int i=1;i<=n;i++)
      cin>>s[i],vis[s[i]]=1;
    cin>>s[0];
    for(int i=0;i<=l-m;i++)
    {
        ss=s[0].substr(i,m);
        if(vis[ss]){ans=i+1;break;}
    }
    if(!ans) printf("no\n");
    else printf("%d\n",ans);
    fclose(stdin);fclose(stdout);
    return 0;
}

 

 

/*
各种情况分析，由于路径权值的相反性
只要有环，要么不走，要么等效完整走整数遍。
假设有k个环，每个环的边权和为xi，那么问题转化为
不定方程a*x1+b*x2+c*x3+....+m*xk=T是否存在整数解。
根据不定方程整数解的条件可知，gcd(x1~xm) | T 时有，否则无。 
*/
#include<bits/stdc++.h>

#define N 411111
#define ll long long

using namespace std;
int n,q;
ll sum[N];
int toedge[N],cnt;
struct Edge
{
    int to,val,next;
};
Edge edge[N<<1];

int read()
{
    int ret=0,neg=1;
    char c=getchar();
    while (c<'0' || c>'9'){if (c=='-') neg=-1;c=getchar();}
    while (c>='0' && c<='9'){ret=ret*10+c-'0';c=getchar();}
    return ret*neg;
}

ll SUM(int x,int y){return sum[y]-sum[x];}
ll Abs(ll x){return x>0 ? x : -x;}
ll gcd(ll x,ll y){return (y==0) ? x : gcd(y,x%y);}

void add(int from,int to,int val)
{
    edge[++cnt]=(Edge)
    {
        to,val,toedge[from]
    };
    toedge[from]=cnt;
}


void dfs(int x,int fa)
{
    for (int i=toedge[x]; i; i=edge[i].next)
    {
        int to=edge[i].to;
        if (to==fa) continue;
        sum[to]=sum[x]+edge[i].val;
        dfs(to,x);
    }
}

int main()
{
    freopen("lab.in","r",stdin);
    freopen("lab.out","w",stdout);
    n=read();q=read();
    int x,y,z;
    for (int i=1; i<n; i++)
    {
        x=read();y=read();z=read();
        add(x,y,z);add(y,x,-z);
    }
    dfs(1,0);int k,t;ll xun=-1;
    for (int i=1; i<=q; i++)
    {
        k=read();x=read();y=read();t=read();
        if (k==0)
        {
            ll tmp=SUM(y,x);
            if (xun==-1) xun=Abs(tmp+t);
            else if (tmp+t!=0) xun=gcd(xun,Abs(tmp+t));
        }
        else
        {
            ll tmp=Abs((ll)t-SUM(x,y));
            if (xun==-1)
                if (tmp==0) puts("yes");
                else puts("no");
            else if (tmp%xun==0) puts("yes");
            else puts("no");
        }
    }
}

 

 

#include<iostream>
#include<cstdio>
#include<cstring>

#define N 100007
#define ll long long

using namespace std;
ll n,m,ans1,ans2,cnt,tot;
ll x,y,z,q;
ll head[N],deep[N],sum[N],f[N][26];
ll in[N],F[N][2],son[N][2];
struct edge{
    ll u,v,w,nxt;
}e[N<<1];

inline ll read()
{
    ll x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

inline void add(int u,int v,int w)
{
    e[++cnt].v=v;e[cnt].w=w;e[cnt].nxt=head[u];head[u]=cnt;
}

void dfs(int now,int fa,int c)
{
    f[now][0]=fa;deep[now]=c;
    for(int i=head[now];i;i=e[i].nxt)
    {
        int v=e[i].v;
        if(v==fa) continue;
        sum[v]=sum[now]+e[i].w;
        dfs(v,now,c+1);
    }
}

void get()
{
    for(int j=1;j<=25;j++) for(int i=1;i<=n;i++)
    f[i][j]=f[f[i][j-1]][j-1];
}

int lca(int a,int b)
{
    if(deep[a]<deep[b]) swap(a,b);
    int t=deep[a]-deep[b];
    for(int i=0;i<=t;i++) 
    if(t&(1<<i)) a=f[a][i];
    if(a==b) return a;
    for(int i=25;i>=0;i--)
    if(f[a][i]!=f[b][i])
    a=f[a][i],b=f[b][i];
    return f[a][0];
}

void solve1()
{
    dfs(1,1,0);get();
    for(int i=1;i<=m;i++)
    {
        tot=ans1=ans2=0;
        q=read();
        for(int j=1;j<=n;j++)
        {
            if(j==q) continue;
            int res=lca(q,j);
            tot=sum[q]+sum[j]-2*sum[res];
            if(tot%2) ans1+=tot;
            else ans2+=tot;
        }
        cout<<ans1<<" "<<ans2<<endl;
    }
}

void dp(int u,int from)//0 偶数 
{
    son[u][0]=son[u][1]=0;
    for(int i=head[u];i;i=e[i].nxt)
    {
        int v=e[i].v;
        if(v==from) continue;dp(v,u);
        if(e[i].w%2==1)
        {
            son[v][1]++;
            if(in[v]==1)
            {
                son[v][1]++;son[u][1]++;
                F[u][0]+=e[i].w*son[v][0];
                F[u][1]+=e[i].w*son[v][1];    
            }
            else
            {
                son[u][1]+=son[v][0],son[u][0]+=son[v][1];
                F[u][0]+=F[v][1]+e[i].w*son[v][1];
                F[u][1]+=F[v][0]+e[i].w*son[v][0];
                F[u][1]+=e[i].w;    
            }
        }
        else
        {
            son[v][0]++;
            if(in[v]==1)
            {
                son[v][0]++;son[u][0]++;
                F[u][0]+=e[i].w*son[v][0];
                F[u][1]+=e[i].w*son[v][1];                
            }
            else
            {
                son[u][0]+=son[v][0],son[u][1]+=son[v][0];
                F[u][0]+=F[v][0]+e[i].w*son[v][0];
                F[u][1]+=F[v][1]+e[i].w*son[v][1];    
                F[u][0]+=e[i].w;            
            }
        }
    }
}


void solve2()
{
    for(int i=1;i<=m;i++)
    {
        q=read();
        memset(f,0,sizeof F);
        memset(son,0,sizeof son);
        dp(q,q);
        cout<<F[q][1]<<" "<<F[q][0]<<endl;
    }
}

int main()
{
    freopen("civilization.in","r",stdin);
    freopen("civilization.out","w",stdout);
    n=read();m=read();
    for(int i=1;i<n;i++)
    {
        x=read();y=read();z=read();
        add(x,y,z);add(y,x,z);
    }
    if(n<=5000) solve1();
    else solve2();
    
    fclose(stdin);fclose(stdout);
    return 0;
}

 

#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

// 70%保证答案不爆int

int n,q;
int H[100005], X[200005], P[200005], w[200005], tot;

inline void add(int x,int y,int z)
{
    P[++tot]=y;
    X[tot]=H[x];
    H[x]=tot;
    w[tot]=z;
}
typedef long long LL;
LL f[2][100005]; // 子树
LL ans[2][100005];
int siz[2][100005]; // 子树
int siz2[2][100005]; // 整棵树

void dfs1(int x,int fa)
{
    siz[0][x] = 1;
    for(int i=H[x]; i; i=X[i])
    {
        if(P[i] == fa) continue;
        dfs1(P[i],x);
        if(w[i]&1)
        {
            siz[0][x] += siz[1][P[i]];
            siz[1][x] += siz[0][P[i]];
            f[0][x] += f[1][P[i]] + w[i]*siz[1][P[i]];
            f[1][x] += f[0][P[i]] + w[i]*siz[0][P[i]];
        }
        else
        {
            siz[0][x] += siz[0][P[i]];
            siz[1][x] += siz[1][P[i]];
            f[0][x] += f[0][P[i]] + w[i]*siz[0][P[i]];
            f[1][x] += f[1][P[i]] + w[i]*siz[1][P[i]];
        }
    }
}

void dfs2(int x,int fa)
{
    for(int i=H[x]; i; i=X[i])
    {
        if(P[i]==fa) continue;
        if(w[i]&1)
        {
            siz2[0][P[i]] = siz2[1][x];
            siz2[1][P[i]] = siz2[0][x];
            ans[0][P[i]] =  f[0][P[i]] +  ans[1][x] - (f[0][P[i]]+w[i]*siz[0][P[i]]) + w[i]*(siz2[1][x]-siz[0][P[i]]) ;
            ans[1][P[i]] =  f[1][P[i]] +  ans[0][x] - (f[1][P[i]]+w[i]*siz[1][P[i]]) + w[i]*(siz2[0][x]-siz[1][P[i]]) ;
        }
        else
        {
            siz2[0][P[i]] = siz2[0][x];
            siz2[1][P[i]] = siz2[1][x];
            ans[0][P[i]] =  f[0][P[i]] +  ans[0][x] - (f[0][P[i]]+w[i]*siz[0][P[i]]) + w[i]*(siz2[0][x]-siz[0][P[i]]) ;
            ans[1][P[i]] =  f[1][P[i]] +  ans[1][x] - (f[1][P[i]]+w[i]*siz[1][P[i]]) + w[i]*(siz2[1][x]-siz[1][P[i]]) ;
        }
        dfs2(P[i],x);
    }
}

int main()
{
    freopen("civilization.in", "r", stdin);
    freopen("civilization.out", "w", stdout);
    scanf("%d%d",&n,&q);
    for(int i=1,x,y,z; i<n; i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);add(y,x,z);
    }
    dfs1(1,0);
    ans[0][1] = f[0][1];ans[1][1] = f[1][1];
    siz2[0][1] = siz[0][1];siz2[1][1] = siz[1][1];
    dfs2(1,0);

    int x;
    while(q--)
    {
        scanf("%d",&x);
        printf("%lld %lld\n",ans[1][x],ans[0][x]);
    }
    fclose(stdout);
    return 0;
}