好困呐(10.4~10.6)
1160 蛇形矩阵
小明玩一个数字游戏,取个n行n列数字矩阵(其中n为不超过100的奇数),数字的填补方法为:在矩阵中心从1开始以逆时针方向绕行,逐圈扩大,直到n行n列填满数字,请输出该n行n列正方形矩阵以及其的对角线数字之和.
n(即n行n列)
n+1行,n行为组成的矩阵,最后一行为对角线数字之和
3
5 4 3
6 1 2
7 8 9
25
/*从右下角开始 i判断走的方向,a,b 是走的位置 p[]判断是不是最外圈。 */ #include<iostream> #include<cstdio> #include<cstring> #define N 101 using namespace std; int a,b,n,cen,str,tot,ans; int num[N][N]; bool flag[N][N],p[5]; int main() { scanf("%d",&n); a=n,b=n,tot=n*n;cen=(n+1)/2; for(int i=1;;) { if(flag[cen][cen] || tot==0) break; if(i==5) i=1; // if(!flag[a][b]) // { if(i==1) { if(!flag[a][b]) flag[a][b]=true,num[a][b]=tot--; else { a--;b++;i++;continue; } if(a==b || a+b==n+1) ans+=(tot+1); if(b>1) b--; else { if(!p[1]) { p[1]=1;a--;i++;continue; } else { a--;b++;i++;continue; } } } if(i==2) { if(!flag[a][b]) flag[a][b]=true,num[a][b]=tot--; else { a++;b++;i++;continue; } if(a==b || a+b==n+1) ans+=(tot+1); if(a>1) a--; else { if(!p[2]) { p[2]=1;b++;i++;continue; } else { a++;b++;i++;continue; } } } if(i==3) { if(!flag[a][b]) flag[a][b]=true,num[a][b]=tot--; else { b--;a++;i++;continue; } if(a==b || a+b==n+1) ans+=(tot+1); if(b<n) b++; else { if(!p[3]) { p[3]=1;a++;i++;continue; } else { b--;a++;i++;continue; } } } if(i==4) { if(!flag[a][b]) flag[a][b]=true,num[a][b]=tot--; else { a--;b--;i++;continue; } if(a==b || a+b==n+1) ans+=(tot+1); if(a<n) a++; else { if(!p[4]) { p[4]=1;b--;i++;continue; } else { a--;b--;i++;continue; } } } } for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { printf("%d ",num[i][j]); if(j==n) printf("\n"); } printf("%d\n",ans); return 0; }
1011 数的计算
2001年NOIP全国联赛普及组
我们要求找出具有下列性质数的个数(包含输入的自然数n):
先输入一个自然数n(n<=1000),然后对此自然数按照如下方法进行处理:
1. 不作任何处理;
2. 在它的左边加上一个自然数,但该自然数不能超过原数的一半;
3. 加上数后,继续按此规则进行处理,直到不能再加自然数为止.
一个数n
满足条件的数的个数
6
6
6个数分别是:
6
16
26
126
36
136


//递推 #include<iostream> #include<cstdio> #include<cstring> #define N 1001 using namespace std; int n,m; int f[N]; int main() { scanf("%d",&n); f[1]=1; for(int i=2;i<=n;i++) { if(i%2==1) f[i]=f[i-1]; else f[i]=f[i-1]+f[i/2]; } printf("%d\n",f[n]); return 0; }
3038 3n+1问题
第一行是一个整数T.表示输入数据的组数.
第二行是T个正整数n.
对于每个正整数n,每行输出一个数s,表示n通过多少步变换会变成1,如果n无法变成1,则输出-1.
3
1 2 3
0
1
7
1 <= T <= 100
1 <= n <= 10000


#include<iostream> #include<cstdio> #include<cstring> using namespace std; long long T,n,m,tot,ans; int dfs(long long now) { if(now==1) return tot; if(now%2==0){ now/=2;tot++; } else { now=3*now+1;tot++; }dfs(now); } int main() { scanf("%d\n",&T); while(T--) { scanf("%d",&n);tot=0; printf("%lld\n",dfs(n)); } return 0; }
1501 二叉树最大宽度和高度
给出一个二叉树,输出它的最大宽度和高度。
第一行一个整数n。
下面n行每行有两个数,对于第i行的两个数,代表编号为i的节点所连接的两个左右儿子的编号。如果没有某个儿子为空,则为0。
输出共一行,输出二叉树的最大宽度和高度,用一个空格隔开。
5
2 3
4 5
0 0
0 0
0 0
2 3
n<16
默认第一个是根节点
以输入的次序为编号
2-N+1行指的是这个节点的左孩子和右孩子
注意:第二题有极端数据!
1
0 0
这题你们别想投机取巧了,给我老老实实搜索!


#include<iostream> #include<cstdio> #include<cstring> #define N 10001 using namespace std; int son[101],head[N],deep[N]; int n,T,x,y,cnt,max1=1,max2=1; bool vis[N]; struct edge{ int u,v,net; }e[N]; inline int read() { int x=0,f=1;char c=getchar(); while(c>'9' || c<'0'){if(c=='-')f=-1;c=getchar();} while(c>='0' && c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } inline void add(int u,int v) { e[++cnt].v=v;e[cnt].net=head[u];head[u]=cnt; } void dfs(int now,int c) { deep[now]=c;max1=max(max1,deep[now]); for(int i=head[now];i;i=e[i].net) { int v=e[i].v; if(vis[v]) continue; vis[v]=1;son[deep[now]]++; dfs(v,c+1); }return; } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { x=read();y=read(); if(x) add(i,x),add(x,i); if(y) add(i,y),add(y,i); } vis[1]=1;dfs(1,1); for(int i=1;i<=n;i++) max2=max(max2,son[i]); printf("%d %d\n",max2,max1); return 0; }
1116 四色问题
给定N(小于等于8)个点的地图,以及地图上各点的相邻关系,请输出用4种颜色将地图涂色的所有方案数(要求相邻两点不能涂成相同的颜色)
数据中0代表不相邻,1代表相邻
第一行一个整数n,代表地图上有n个点
接下来n行,每行n个整数,每个整数是0或者1。第i行第j列的值代表了第i个点和第j个点之间是相邻的还是不相邻,相邻就是1,不相邻就是0.
我们保证a[i][j] = a[j][i] (a[i,j] = a[j,i])
染色的方案数
8
0 0 0 1 0 0 1 0
0 0 0 0 0 1 0 1
0 0 0 0 0 0 1 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
1 0 1 0 0 0 0 0
0 1 0 0 0 0 0 0
15552
n<=8


/* dfs,回溯 */ #include<iostream> #include<cstdio> #include<cstring> #define N 10 using namespace std; bool vis; int col[N],a[N][N]; int n,ans,pre,pot; inline int read() { int x=0,f=1;char c=getchar(); while(c>'9' || c<'0'){if(c=='-')f=-1;c=getchar();} while(c>='0' && c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } void dfs(int now) { if(now==n+1){ans++;return;} for(int i=1;i<=4;i++) { vis=0; for(int j=1;j<now;j++) { if(a[now][j] && col[j]==i){vis=1;break;} } if(vis) continue; col[now]=i;dfs(now+1);col[now]=0; } } int main() { n=read(); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) a[i][j]=read(); dfs(1); printf("%d\n",ans); return 0; }
1344 线型网络
有 N ( <=20 ) 台 PC 放在机房内,现在要求由你选定一台 PC,用共 N-1 条网线从这台机器开始一台接一台地依次连接他们,最后接到哪个以及连接的顺序也是由你选定的,为了节省材料,网线都拉直。求最少需要一次性购买多长的网线。(说白了,就是找出 N 的一个排列 P1 P2 P3 ..PN 然后 P1 -> P2 -> P3 -> ... -> PN 找出 |P1P2|+|P2P3|+...+|PN-1PN| 长度的最小值)
第一行 N ,下面 N 行,每行分别为机器的坐标(x,y) ( 实数 -100<=x,y<=100 )
最小的长度,保留两位小数。
3
0 0
1 1
1 -1
2.83


/* 40分 暴力dfs 并查集维护已经连到的点 */ #include<iostream> #include<cstdio> #include<cstring> #include<cmath> #define N 101 using namespace std; double ans,pre,cur[N][N]; int n,cnt; int vis[N][N],f[N]; struct node { int x,y; }p[N]; double min(double a,double b) { if(a>b) return b; else return a; } double work(node a,node b) { double xx=a.x-b.x;if(xx<0) xx=-xx; xx=xx*xx; double yy=a.y-b.y;if(yy<0) yy=-yy; yy=yy*yy; double tmp=sqrt(xx+yy); return tmp; } inline int find(int x) { if(x==f[x]) return x; else return find(f[x]); } void dfs(int now) { if(cnt==n-1){ans=min(ans,pre);return;} for(int i=1;i<=n;i++) { if(i==now || f[find(now)]==f[find(i)]) continue; cur[now][i]=cur[i][now]=work(p[now],p[i]); pre+=cur[now][i]; cnt++;f[i]=now;dfs(i); pre=pre-cur[now][i];cnt--;f[i]=i; } } int main() { scanf("%d",&n);ans=0x3f3f3f3f; for(int i=1;i<=n;i++) scanf("%d%d",&p[i].x,&p[i].y); for(int i=1;i<=n;i++) { cnt=0;pre=0; for(int j=1;j<=n;j++) f[j]=j; dfs(i); } printf("%.2lf\n",ans); return 0; }
1983 等式问题
有一个未完成的等式:1 2 3 4 5 6 7 8 9=N 空格(1前面没有空格)内可以填入+,-,也可以不填。 编程找出输入某个整数 N 后使等式成立的所有方案的总数。保证有解。
输入一个数N。
输出一个数。所有的方案数。
108
15


#include<cstdio> #include<iostream> using namespace std; int n,sum; void dfs(int k,int t) { if(t==n&&k>9){sum++;return;} int tmp=0; for(int i=k; i<=9; i++) { tmp=tmp*10+i; dfs(i+1,t+tmp); if(k!=1) dfs(i+1,t-tmp); } } int main() { scanf("%d",&n); dfs(1,0); printf("%d\n",sum); return 0; }
2843 拯救炜哥
有一天,炜哥和欧能干一起去大魔王家里做(dao)客(luan),不巧被魔王发现了。魔王将炜哥和欧能干抓走了,关在了两个不同的房间里。魔王听说吃炜哥的肉可以长生不老(炜哥=唐僧?),于是开始准备晚饭。由于魔王疏忽,将一把钥匙漏在了欧能干的房间里。欧能干知道这个消息后,赶紧去拯救炜哥。炜哥生命危在旦夕,欧能干必须马上离开这个房间,救出炜哥。于是他找到了编程大牛的你。
第一行输入两个数字,分别代表房间的长和宽;
第二~第n+1行 输入房间的摆设
o 代表欧能干现在的位置;
k 代表钥匙(key)
d 代表房间的门
. 代表空地(可以直接经过的地)
* 代表墙(不能穿过)
一个数:最少要走几个格子
如果无法逃出则输出 No Way
3 3
o.k
d*.
...
5
1<=n,m<=1000


/* o->k最短路+k->d最短路 bfs 最后一个测试点有误 */ #include<iostream> #include<cstdio> #include<cstring> #define inf 0x3f3f3f3f #define N 1001 using namespace std; int n,m,sx1,sy1,sx,sy,sx2,sy2; int head,tail,ans1,ans2,flag,opt; int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; int map[N][N],vis[N][N]; char ch; struct node { int x,y,st; }q[N<<1]; void bfs(int x,int y) { vis[x][y]=1;head=tail=1; q[tail].x=x;q[tail].y=y;q[tail++].st=0; while(head<=tail) { node u=q[head++]; for(int i=0;i<4;i++) { int xx=u.x+dx[i],yy=u.y+dy[i]; if(!vis[xx][yy] && xx>=1 && yy>=1 && xx<=n && yy<=m && map[xx][yy]!=1) { node tmp;tmp.x=xx;tmp.y=yy; tmp.st=u.st+1;vis[xx][yy]=1; if(xx==sx2 && yy==sy2 && flag) ans1=min(ans1,tmp.st),opt++; if(xx==sx1 && yy==sy1 && !flag) ans2=min(ans2,tmp.st),opt++; q[tail++]=tmp; } } } } int main() { scanf("%d%d",&m,&n);ans1=ans2=inf; if(m==10 && n==6) {printf("No Way\n");return 0;} for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { cin>>ch; if(ch=='*') map[i][j]=1; if(ch=='o') sx=i,sy=j; if(ch=='k') sx1=i,sy1=j; if(ch=='d') sx2=i,sy2=j; } flag=0;bfs(sx,sy); memset(q,0,sizeof q); memset(vis,0,sizeof vis); flag=1;bfs(sx1,sy1); if(opt==2)printf("%d\n",ans1+ans2); else printf("No Way\n"); return 0; }
-----------------------------------------------------------------------------————————————————————————————————————————————————————————————
P3088 [USACO13NOV]挤奶牛Crowded Cows
题目描述
Farmer John's N cows (1 <= N <= 50,000) are grazing along a one-dimensional fence. Cow i is standing at location x(i) and has height h(i) (1 <= x(i),h(i) <= 1,000,000,000).
A cow feels "crowded" if there is another cow at least twice her height within distance D on her left, and also another cow at least twice her height within distance D on her right (1 <= D <= 1,000,000,000). Since crowded cows produce less milk, Farmer John would like to count the number of such cows. Please help him.
FJ有N(1 <= N <= 50,000)头奶牛沿着一维的栅栏吃草,第i头奶牛在目标点x(i) ,它的身高是 h(i) (1 <=x(i),h(i) <= 1,000,000,000)。
当一头奶牛左边D距离内而且右边D距离内有身高至少是它的两倍的奶牛,t (1 <= D <= 1,000,000,000),它就会觉得拥挤。
请计算觉得拥挤的奶牛的数量。
输入输出格式
输入格式:
* Line 1: Two integers, N and D.
* Lines 2..1+N: Line i+1 contains the integers x(i) and h(i). The locations of all N cows are distinct.
输出格式:
* Line 1: The number of crowded cows.
输入输出样例
说明
There are 6 cows, with a distance threshold of 4 for feeling crowded. Cow #1 lives at position x=10 and has height h=3, and so on.
The cows at positions x=5 and x=6 are both crowded.


/* 36分暴力 */ #include<iostream> #include<cstdio> #include<cstring> #define N 10000000 using namespace std; long long n,m,d,ans,cnt; long long h[N],x[N]; bool flag; int main() { freopen("data.txt","r",stdin); freopen("T1b.txt","w",stdout); scanf("%lld%lld",&n,&d); for(int i=1;i<=n;i++) { scanf("%lld",&x[i]); scanf("%lld",&h[x[i]]); m=max(m,x[i]); } for(int i=1;i<=m;i++) { if(h[i]) { flag=0; for(int j=i;j>0 && j>=i-d;j--) if(h[j]>=2*h[i]) {flag=1;break;} for(int j=i;j<=m && j<=i+d;j++) if(h[j]>=2*h[i] && flag) {cnt++;break;} } } printf("%lld\n",cnt); return 0; }


/* 45分暴力 */ #include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 10000001 #define LL long long using namespace std; LL n,m,d,ans,cnt; int a[3001][3001]; bool flag; struct node{ LL x,h; bool operator < (const node &a) const{ return x<a.x; } }Cow[N]; int main() { scanf("%lld%lld",&n,&d); for(int i=1;i<=n;i++) cin>>Cow[i].x>>Cow[i].h; sort(Cow+1,Cow+n+1); for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) a[i][j]=a[j][i]=Cow[j].x-Cow[i].x; for(int i=1;i<=n;i++) { flag=0; for(int j=i-1;j;j--) { if(a[j][i]>d) break; if(Cow[i].h*2<=Cow[j].h) flag=1; } if(!flag) continue; for(int j=i+1;j<=n;j++) { if(a[j][i]>d) break; if(Cow[i].h*2<=Cow[j].h) {cnt++;break;} } } printf("%lld\n",cnt); return 0; }


/* 类似滑动窗口 单调队列维护一个点左区间和右区间最大值,判断。 */ #include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 50001 using namespace std; int n,m,d,ans,cnt; bool f1[N],f2[N]; struct node{ int h,x; bool operator < (const node &a) const { return x<a.x; } }Cow[N],q[N]; int main() { scanf("%d%d",&n,&d); for(int i=1;i<=n;i++) scanf("%d%d",&Cow[i].x,&Cow[i].h); sort(Cow+1,Cow+n+1); int l=1,r=1; for(int i=1;i<=n;i++) { while(l<r && q[r-1].h<Cow[i].h) r--; q[r++]=Cow[i]; while(l<r && Cow[i].x-q[l].x>d) l++; if(q[l].h>=Cow[i].h*2 && l<=r) f1[i]=1; } memset(q,0,sizeof q); l=1;r=1; for(int i=n;i>=1;i--) { while(l<r && q[r-1].h<Cow[i].h) r--; q[r++]=Cow[i]; while(l<r && q[l].x-Cow[i].x>d) l++; if(q[l].h>=Cow[i].h*2 && l<=r) f2[i]=1; } for(int i=1;i<=n;i++) if(f1[i] && f2[i]) ans++; printf("%d\n",ans); return 0; }
P1714 切蛋糕
题目描述
今天是小Z的生日,同学们为他带来了一块蛋糕。这块蛋糕是一个长方体,被用不同色彩分成了N个相同的小块,每小块都有对应的幸运值。
小Z作为寿星,自然希望吃到的第一块蛋糕的幸运值总和最大,但小Z最多又只能吃M小块(M≤N)的蛋糕。
吃东西自然就不想思考了,于是小Z把这个任务扔给了学OI的你,请你帮他从这N小块中找出连续的k块蛋糕(k≤M),使得其上的幸运值最大。
输入输出格式
输入格式:
输入文件cake.in的第一行是两个整数N,M。分别代表共有N小块蛋糕,小Z最多只能吃M小块。
第二行用空格隔开的N个整数,第i个整数Pi代表第i小块蛋糕的幸运值。
输出格式:
输出文件cake.out只有一行,一个整数,为小Z能够得到的最大幸运值。
输入输出样例
说明
对20%的数据,N≤100。
对100%的数据,N≤500000,|Pi|≤500。 答案保证在2^31-1之内。


/* 40暴力 */ #include<iostream> #include<cstdio> #include<cstring> #define N 500001 using namespace std; int sum[N],a[N]; int n,m,k,l,r,ans,cnt; int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&a[i]),sum[i]=sum[i-1]+a[i]; int res=0; for(int i=1;i<=n;i++) for(int j=i+1;j<=i+m;j++) res=max(res,sum[j]-sum[i]); printf("%d\n",res); return 0; }


/* f[i]表示以i结尾的最大和 f[i]=max(sum[i]-sum[j]) i-m <= j <= i 单调队列每次更新最小的sum[j] 注意队列边界问题! */ #include<iostream> #include<cstdio> #include<cstring> #define N 500001 using namespace std; int n,m,ans,cnt; int sum[N],f[N],q[N]; int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&f[i]),sum[i]=sum[i-1]+f[i]; int l=1,r=1,res=0; for(int i=1;i<=n;i++) { while(l<r && sum[q[r-1]]>sum[i]) r--; q[r++]=i; while(l<r && i-q[l]>m) l++; f[i]=max(f[i],sum[i]-sum[q[l]]); } for(int i=1;i<=n;i++) res=max(res,f[i]); printf("%d\n",res); return 0; }
、
P2422 良好的感觉
题目描述
kkk做了一个人体感觉分析器。每一天,人都有一个感受值Ai,Ai越大,表示人感觉越舒适。在一段时间[i, j]内,人的舒适程度定义为[i, j]中最不舒服的那一天的感受值 * [i, j]中每一天感受值的和。现在给出kkk在连续N天中的感受值,请问,在哪一段时间,kkk感觉最舒适?
输入输出格式
输入格式:
第一行为N,代表数据记录的天数
第二行N个整数,代表每一天的感受值
输出格式:
一行,表示在最舒适的一段时间中的感受值。
输入输出样例
说明
样例解释:
kkk最开心的一段时间是第3天到第5天,开心值:(6+4+5)*4=60
对于30%的数据,1<=N<=100
对于70%的数据,1<=N<=2000
对于100%的数据,1<=N<=100000,1<=感受值<=1000000


/* 单调栈 不开long long 爆零 */ #include<iostream> #include<cstdio> #include<cstring> #include<stack> #define ll long long #define N 100001 using namespace std; ll n,now,ans,cnt; ll sum[N],q[N],a[N],Left[N],Right[N]; stack<ll>st; int main() { scanf("%lld",&n); for(int i=1;i<=n;i++) scanf("%lld",&a[i]),sum[i]=sum[i-1]+a[i]; st.push(1); for(int i=2;i<=n;i++) { if(!st.empty()) now=st.top(); if(st.empty()) st.push(i),now=i; if(a[now]<a[i]) Left[i]=now,st.push(i); else { while(!st.empty() && a[now]>a[i]) { st.pop();Right[now]=i; if(!st.empty()) now=st.top(); } if(st.empty()) Left[i]=0; else Left[i]=now; st.push(i); } } for(int i=1;i<=n;i++) if(Right[i]==0) Right[i]=n+1; for(int i=1;i<=n;i++) ans=max(ans,a[i]*(sum[Right[i]-1]-sum[Left[i]])); printf("%lld\n",ans); return 0; }
P2947 [USACO09MAR]向右看齐Look Up
题目描述
Farmer John's N (1 <= N <= 100,000) cows, conveniently numbered 1..N, are once again standing in a row. Cow i has height H_i (1 <= H_i <= 1,000,000).
Each cow is looking to her left toward those with higher index numbers. We say that cow i 'looks up' to cow j if i < j and H_i < H_j. For each cow i, FJ would like to know the index of the first cow in line looked up to by cow i.
Note: about 50% of the test data will have N <= 1,000.
约翰的N(1≤N≤10^5)头奶牛站成一排,奶牛i的身高是Hi(l≤Hi≤1,000,000).现在,每只奶牛都在向右看齐.对于奶牛i,如果奶牛j满足i<j且Hi<Hj,我们可以说奶牛i可以仰望奶牛j. 求出每只奶牛离她最近的仰望对象.
Input
输入输出格式
输入格式:
* Line 1: A single integer: N
* Lines 2..N+1: Line i+1 contains the single integer: H_i
第 1 行输入 N,之后每行输入一个身高 H_i。
输出格式:
* Lines 1..N: Line i contains a single integer representing the smallest index of a cow up to which cow i looks. If no such cow exists, print 0.
共 N 行,按顺序每行输出一只奶牛的最近仰望对象,如果没有仰望对象,输出 0。
输入输出样例
说明
FJ has six cows of heights 3, 2, 6, 1, 1, and 2.
Cows 1 and 2 both look up to cow 3; cows 4 and 5 both look up to cow 6; and cows 3 and 6 do not look up to any cow.
【输入说明】6 头奶牛的身高分别为 3, 2, 6, 1, 1, 2.
【输出说明】奶牛#1,#2 仰望奶牛#3,奶牛#4,#5 仰望奶牛#6,奶牛#3 和#6 没有仰望对象。
【数据规模】
对于 20%的数据: 1≤N≤10;
对于 50%的数据: 1≤N≤1,000;
对于 100%的数据:1≤N≤100,000;1≤H_i≤1,000,000;


/* 单调栈 */ #include<iostream> #include<cstdio> #include<cstring> #define N 100001 using namespace std; int a,n,top=1; int ans[N]; struct node{ int hao,shu; }sta[N]; int main() { scanf("%d",&n); for(int i=1; i<=n; i++) { scanf("%d",&a); while(a>sta[top-1].shu&&top>1) { ans[sta[top-1].hao]=i; top--; } sta[top].shu=a; sta[top].hao=i; top++; } for(int i=1; i<=n; i++) cout<<ans[i]<<endl; return 0; }
P2629 好消息,坏消息
题目描述
uim在公司里面当秘书,现在有n条消息要告知老板。每条消息有一个好坏度,这会影响老板的心情。告知完一条消息后,老板的心情等于之前老板的心情加上这条消息的好坏度。最开始老板的心情是0,一旦老板心情到了0以下就会勃然大怒,炒了uim的鱿鱼。
uim为了不被炒,知道了了这些消息(已经按时间的发生顺序进行了排列)的好坏度,希望研究如何不让老板发怒。
uim必须按照时间的发生顺序逐条将消息告知给老板。不过uim可以使用一种叫“倒叙”的手法,例如有n条消息,小a可以从k,k+1,k+2...n,1,2...k-1这种顺序通报。
他希望知道,有多少个k,从k开始通报到n然后从1通报到k-1可以让老板不发怒。
输入输出格式
输入格式:
第一行一个整数n(1 <= n <= 10^6),表示有n个消息。
第二行n个整数,按时间顺序给出第i条消息的好坏度Ai(-1000 <= Ai <= 1000)
输出格式:
一行一个整数,表示可行的方案个数。
输入输出样例
说明
样例解释
[5 1 2 -3]或[1 2 -3 5]
对于25%数据n<=1000
对于75%数据n<=10000
对于100%数据n<=10^6


/* 75暴力 */ #include<iostream> #include<cstdio> #include<cstring> #define N 1000001 using namespace std; int n,m,ans,cnt,flag; int sum[N],a[N],opt[N]; int main() { freopen("data.txt","r",stdin); freopen("2.out","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]),sum[i]=sum[i-1]+a[i]; for(int i=1;i<=n;i++) { flag=0; for(int j=i;j<=n;j++) if(sum[j]-sum[i-1]<0) flag=1; if(!flag) opt[i]=1; } for(int i=1;i<=n;i++) { flag=0; if(opt[i]) { for(int j=1;j<=i;j++) if(sum[j]+sum[n]-sum[i-1]<0) flag=1; if(!flag) cnt++; } } printf("%d\n",cnt); return 0; }


/* f[i]表示以i开头的后缀最小值 先筛选出f[i]>=0的点,再用单调队列维护前缀和最小值 只需要i+1~n的和加上前缀和最小值>=0即可。前缀最小值的下标到i这段不必考虑。 */ #include<iostream> #include<cstdio> #include<cstring> #define N 1000001 using namespace std; int n,m,ans,cnt; int a[N],sum[N],q[N],f[N],flag[N]; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]),sum[i]=sum[i-1]+a[i]; for(int i=n;i>=0;i--) f[i]=min(a[i],a[i]+f[i+1]); for(int i=1;i<=n;i++) if(f[i]>=0) flag[i]=1;flag[1]=1; int l=1,r=1; for(int i=1;i<=n;i++) { if(sum[n]-sum[i]<0) continue; while(l<r && sum[q[r-1]]>sum[i]) r--; q[r++]=i; if(l<r && sum[q[l]]+sum[n]-sum[i]>=0 && flag[i==n?1:i+1]) cnt++; } printf("%d\n",cnt); return 0; }
————————————————————————————————————————————————————————————————————————————————————————
P4888 三去矩阵
题目背景
无
题目描述
现在小Y有个l \times ll×l的正方形字母矩阵,现在他想进行qq次询问,每次询问最长的以(x_i,y_i)(xi,yi)为中心的在一条水平或竖直的直线上的回文串的长度。
输入输出格式
输入格式:
第一行输入两个整数l,ql,q,分别表示矩阵的边长和询问的个数。
接下来的ll行,每行ll个字母,表示这个矩阵上的字母。
接下来的qq行,每行两个整数x_i,y_ixi,yi,表示第ii个询问为在询问矩阵中最长的以(x_i,y_i)(xi,yi)为中心的在一条直线上的回文串的长度。
输出格式:
输出qq行,第ii行为对于第ii个询问的回答。
输入输出样例
说明
对于20\%20%的数据,1 \le l \le 21≤l≤2
另有20\%20%的数据,q = 1q=1
另有20\%20%的数据,字母矩阵中心对称,上下对称,左右对称且对角线对称。
对于100\%100%的数据,1 \le l,q \le 20001≤l,q≤2000,字母只有小写字母。


/* 字符串模拟 */ #include<iostream> #include<cstdio> #include<cstring> #define N 2001 using namespace std; int n,m,x,y,T,ans,cnt; char s[N][N]; int a[N][N]; int main() { scanf("%d%d",&n,&T); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>s[i][j]; for(int i=1;i<=n;i++) { int res=0; for(int j=1;j<=n;j++) { int k=0;res=0; while(j+k<=n && j-k>=0 && s[i][j+k]==s[i][j-k]) k++; res=max(res,k*2-1);k=0; while(i+k<=n && i-k>=0 && s[i+k][j]==s[i-k][j]) k++; res=max(res,k*2-1); a[i][j]=res; } } while(T--) { cin>>x>>y; printf("%d\n",a[x][y]); } return 0; }
P4889 kls与flag
题目背景
kls毒奶非常厉害。
题目描述
有nn个OI选手,每个人插了一个flag。有一天因为某种原因,flag都被触发了,所以地上有一排nn根竹竿,竹竿的间距均为一个单位长度,高度在1\sim m1∼m之间。
kls看到这些竹竿,感觉不好看,于是准备把它们全部放倒。
在这之前,kls想到了一个数学问题。每根竹竿可以往左倒或者往右倒。如果两根竹竿在选择方向放倒之后,它们的顶端可以重合,那么称它们是优秀的。现在kls想要知道,有多少对竹竿是优秀的。
输入输出格式
输入格式:
第一行两个数n,mn,m,表示竹竿的个数和最大高度。
第二行nn个正整数,表示每根竹竿的高度。
输出格式:
输出一行,只有一个数,表示有多少对竹竿是优秀的。
输入输出样例
说明
样例解释

- 1号和2号向左倒可以顶端重合
- 4号和5号向右倒可以顶端重合
- 1号向右,5号向左可以顶端重合
数据范围
对于30%的数据,满足n\le 2000n≤2000,m\le 5000m≤5000;
对于60%的数据,满足n\le 200000n≤200000,m\le 500000m≤500000;
对于100%的数据,满足n \le 200000n≤200000,m \le 10^9m≤109。


/* 30暴力 */ #include<iostream> #include<cstdio> #include<cstring> #define N 1000007 #define ll long long using namespace std; ll n,m,ans,cnt; ll v[N],a[N],h[N]; int main() { scanf("%lld%lld",&n,&m); for(int i=1;i<=n;i++) scanf("%lld",&h[i]); for(int i=1;i<=n;i++) v[i-h[i]+500001]++; for(int i=1;i<=n;i++) v[i+h[i]+500001]++; for(int i=0;i<=1000000;i++) if(v[i]) ans+=(v[i]*(v[i]-1)/2); printf("%lld\n",ans); return 0; }


/* 老了 没想到用map 也可以把倒下的坐标记到数组里 */ #include<iostream> #include<cstdio> #include<map> #define N 200007 using namespace std; long long sum; int a[N]; map<int,int> l; int main() { int n,m; scanf("%d %d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=n;i++) { sum+=l[i+a[i]]; l[i+a[i]]++; sum+=l[i-a[i]]; l[i-a[i]]++; } printf("%lld",sum); return 0; }
P3958 奶酪
题目描述
现有一块大奶酪,它的高度为 hh,它的长度和宽度我们可以认为是无限大的,奶酪 中间有许多 半径相同 的球形空洞。我们可以在这块奶酪中建立空间坐标系,在坐标系中, 奶酪的下表面为z = 0z=0,奶酪的上表面为z = hz=h。
现在,奶酪的下表面有一只小老鼠 Jerry,它知道奶酪中所有空洞的球心所在的坐 标。如果两个空洞相切或是相交,则 Jerry 可以从其中一个空洞跑到另一个空洞,特别 地,如果一个空洞与下表面相切或是相交,Jerry 则可以从奶酪下表面跑进空洞;如果 一个空洞与上表面相切或是相交,Jerry 则可以从空洞跑到奶酪上表面。
位于奶酪下表面的 Jerry 想知道,在 不破坏奶酪 的情况下,能否利用已有的空洞跑 到奶酪的上表面去?
空间内两点P_1(x_1,y_1,z_1)P1(x1,y1,z1)、P2(x_2,y_2,z_2)P2(x2,y2,z2)的距离公式如下:
\mathrm{dist}(P_1,P_2)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}dist(P1,P2)=(x1−x2)2+(y1−y2)2+(z1−z2)2
输入输出格式
输入格式:
每个输入文件包含多组数据。
的第一行,包含一个正整数 TT,代表该输入文件中所含的数据组数。
接下来是 TT 组数据,每组数据的格式如下: 第一行包含三个正整数 n,hn,h 和 rr,两个数之间以一个空格分开,分别代表奶酪中空 洞的数量,奶酪的高度和空洞的半径。
接下来的 nn 行,每行包含三个整数 x,y,zx,y,z,两个数之间以一个空格分开,表示空 洞球心坐标为(x,y,z)(x,y,z)。
输出格式:
TT 行,分别对应 TT 组数据的答案,如果在第 ii 组数据中,Jerry 能从下 表面跑到上表面,则输出Yes,如果不能,则输出No (均不包含引号)。
输入输出样例
说明
【输入输出样例 1 说明】
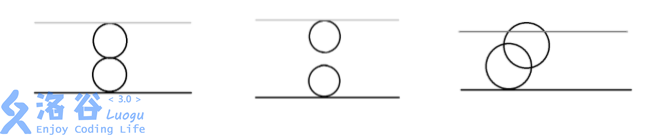
第一组数据,由奶酪的剖面图可见:
第一个空洞在(0,0,0)(0,0,0)与下表面相切
第二个空洞在(0,0,4)(0,0,4)与上表面相切 两个空洞在(0,0,2)(0,0,2)相切
输出 Yes
第二组数据,由奶酪的剖面图可见:
两个空洞既不相交也不相切
输出 No
第三组数据,由奶酪的剖面图可见:
两个空洞相交 且与上下表面相切或相交
输出 Yes
【数据规模与约定】
对于 20\%20%的数据,n = 1n=1,1 \le h1≤h , r \le 10,000r≤10,000,坐标的绝对值不超过 10,00010,000。
对于 40\%40%的数据,1 \le n \le 81≤n≤8, 1 \le h1≤h , r \le 10,000r≤10,000,坐标的绝对值不超过 10,00010,000。
对于80\%80%的数据, 1 \le n \le 1,0001≤n≤1,000, 1 \le h , r \le 10,0001≤h,r≤10,000,坐标的绝对值不超过10,00010,000。
对于 100\%100%的数据,1 \le n \le 1,0001≤n≤1,000,1 \le h , r \le 1,000,000,0001≤h,r≤1,000,000,000,T \le 20T≤20,坐标的 绝对值不超过 1,000,000,0001,000,000,000。


/* bfs 也可以用并查集做 dis 不开long long会挂掉20分 */ #include<iostream> #include<cstdio> #include<cstring> #include<queue> #include<cmath> #define N 1007 #define ll long long using namespace std; ll n,m,h,r; ll x[N],y[N],z[N]; double dis[N][N]; bool vis[N]; queue<int>q; void clear() { memset(dis,0,sizeof dis); memset(x,0,sizeof x); memset(y,0,sizeof y); memset(z,0,sizeof z); memset(vis,0,sizeof vis); while(!q.empty()) q.pop(); } double work(int a,int b) { ll res1=(x[a]-x[b])*(x[a]-x[b]); ll res2=(y[a]-y[b])*(y[a]-y[b]); ll res3=(z[a]-z[b])*(z[a]-z[b]); return double(sqrt(res1+res2+res3)); } bool Bfs() { while(!q.empty()) { int now=q.front();q.pop(); if(h-z[now]<=r) return true; for(int i=1;i<=n;i++) { if(i==now) continue; if(!vis[i] && dis[now][i]<=2*r) vis[i]=1,q.push(i); } } return false; } int main() { int T;scanf("%d",&T); while(T--) { clear(); cin>>n>>h>>r; for(int i=1;i<=n;i++) cin>>x[i]>>y[i]>>z[i]; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) dis[i][j]=dis[j][i]=work(i,j); for(int i=1;i<=n;i++) if(z[i]-r<=0 && !vis[i]) q.push(i),vis[i]=1; bool flag=Bfs(); if(flag) printf("Yes\n"); else printf("No\n"); } return 0; }
P3887 [GDOI2014]世界杯
题目描述
3014年世界杯足球赛就要开始了!作为卫冕冠军中国足球队的教练,手下每位球员都是猛将,如何摆出最强的11人阵容也是一件幸福的烦恼事啊。
众所周知,足球阵容里的11个球员都会被分配到场上某一个特别的位置,而这些位置主要分为守门员、后卫、中场和前锋四种,其中守门员有且只有一个,后卫、中场和前锋的人数取决于你安排的足球阵型。形容足球阵型的方法由后卫开始计算至前锋,但不把守门员计算在内。例如,3-5-2阵型是指有三个后卫、五个中场及两名前锋。由于竞争激烈,每位球员只会培养其中一种位置所需要的技能,所以他们每个人都只能胜任四个位置中的其中一种。
作为一个对球员能力了如指掌的教练,你给每个球员的综合水平进行量化。为了将阵型安排得更好,你的教练团队决定使用以下策略安排球员:首先按照顺序提出Q个阵型,分别代表第一阵型、第二阵型、……、第Q阵型。然后对于每个阵型,从仍未选择的球员中选择最好的对应数量的守门员、后卫、中场和前锋。比如说,对于第一阵型,在所有球员中选择;对于第二阵型,在除了第一阵型外的所有球员中选择;对于第三阵型,在除了第一阵型和第二阵型外的所有球员中选择;以此类推。
现在Q个阵型都已经确定,而你需要知道的,是每个阵型的平均综合水平分别是多少。
输入输出格式
输入格式:
第一行有四个整数K, D, M, F,分别表示守门员、后卫、中场和前锋供挑选的球员人数。
第二行有K个整数k_i,分别表示每个守门员的综合水平值。
第三行有D个整数d_i,分别表示每个后卫的综合水平值。
第四行有M个整数m_i,分别表示每个中场的综合水平值。
第五行有F个整数f_i,分别表示每个前锋的综合水平值。
第六行有一个整数Q,表示教练团队提出的阵型个数。
以下Q行,第i行三个整数A_i, B_i, C_i,由空格间隔,表示第i阵型是A_i - B_i - C_i阵型。
输出格式:
输出Q行。对于第i种阵型,输出一个实数,表示该阵型平均综合水平的最大值,并四舍五入到小数点后2位。
输入输出样例
3 10 12 4 76 60 87 78 84 84 84 81 82 72 51 77 57 85 84 62 87 88 64 81 90 80 66 88 85 65 83 63 79 2 4 5 1 4 4 2
85.64 78.00
说明
对于30%数据,K, D, M, F≤1000,Q≤10;
对于100%数据,1≤K, D, M, F≤10^5,0≤k_i, d_i, m_i, f_i≤10^8,1≤Q≤K,0≤A_i, B_i, C_i≤10,A_i+B_i+C_i=10,∑A_i≤D,∑B_i≤M,∑C_i≤F。


/* 优先队列模拟 */ #include<iostream> #include<cstdio> #include<cstring> #include<queue> #define N 100001 using namespace std; int n,m,x,y,z,ans,cnt; int b_,c_,d_; int a[N],b[N],c[N],d[N]; priority_queue<int>A; priority_queue<int>B; priority_queue<int>C; priority_queue<int>D; inline int read() { int x=0,f=1;char c=getchar(); while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int main() { n=read();m=read();x=read();y=read(); for(int i=1;i<=n;i++) a[i]=read(),A.push(a[i]); for(int i=1;i<=m;i++) b[i]=read(),B.push(b[i]); for(int i=1;i<=x;i++) c[i]=read(),C.push(c[i]); for(int i=1;i<=y;i++) d[i]=read(),D.push(d[i]); z=read();double res=0.00; for(int i=1;i<=z;i++) { res=0; b_=read();c_=read();d_=read(); while(b_--) res+=B.top(),B.pop(); while(c_--) res+=C.top(),C.pop(); while(d_--) res+=D.top(),D.pop(); res+=A.top();A.pop(); res/=11; printf("%.2lf\n",res); } return 0; }
1216: [HNOI2003]操作系统
Time Limit: 10 Sec Memory Limit: 162 MB
Submit: 1172 Solved: 649
Description
写一个程序来模拟操作系统的进程调度。假设该系统只有一个CPU,每一个进程的到达时间,执行时间和运行优先级都是已知的。其中运行优先级用自然数表示,数字越大,则优先级越高。如果一个进程到达的时候CPU是空闲的,则它会一直占用CPU直到该进程结束。除非在这个过程中,有一个比它优先级高的进程要运行。在这种情况下,这个新的(优先级更高的)进程会占用CPU,而老的只有等待。如果一个进程到达时,CPU正在处理一个比它优先级高或优先级相同的进程,则这个(新到达的)进程必须等待。一旦CPU空闲,如果此时有进程在等待,则选择优先级最高的先运行。如果有多个优先级最高的进程,则选择到达时间最早的。
Input
输入文件包含若干行,每一行有四个自然数(均不超过108),分别是进程号,到达时间,执行时间和优先级。不同进程有不同的编号,不会有两个相同优先级的进程同时到达。输入数据已经按到达时间从小到大排序。输入数据保证在任何时候,等待队列中的进程不超过15000个。
Output
按照进程结束的时间输出每个进程的进程号和结束时间
Sample Input
2 10 5 1
3 12 7 2
4 20 2 3
5 21 9 4
6 22 2 4
7 23 5 2
8 24 2 4
Sample Output
3 19
5 30
6 32
8 34
4 35
7 40
2 42


/* 模拟思路比较难想 可以在线操作 重点是如何维护当前时间now 详见代码 */ #include<iostream> #include<cstdio> #include<cstring> #include<queue> #define N 100010 using namespace std; int n,m,ans,cnt; struct node{ int pos,st,ed,tim; friend bool operator < (node a,node b){ return a.tim==b.tim?a.st>b.st:a.tim<b.tim; } }x; priority_queue<node>q; int main() { int a,b,c,d,now=0; while(scanf("%d%d%d%d",&a,&b,&c,&d)!=EOF) { node tmp;tmp.pos=a,tmp.st=b,tmp.ed=c,tmp.tim=d; while(!q.empty()) { x=q.top();q.pop(); if(x.ed+now<=b) { now+=x.ed; printf("%d %d\n",x.pos,now); } else { x.ed-=(b-now),q.push(x); break; } } q.push(tmp);now=b; } while(!q.empty()) { x=q.top();q.pop(); now+=x.ed; printf("%d %d\n",x.pos,now); } return 0; }
P3419 [POI2005]SAM-Toy Cars
题目描述
Johnny is a little boy - he is only three years old and enjoys playing with toy cars very much. Johnny has nn different cars. They are kept on a shelf so high, that Johnny cannot reach it by himself. As there is little space in his room, at no moment may there be more than kk toy cars on the floor.
Johnny plays with one of the cars on the floor. Johnny's mother remains in the room with her son all the time. When Johnny wants to play with another car that is on the floor, he reaches it by himself. But when the toy is on the shelf, his mummy has to hand it to him. When she gives Johnny one car, she can at the same time pick any car from the floor and put it back on the shelf (so that there remains sufficient space on the floor).
The mother knows her child very well and therefore can predict perfectly which cars Johnny will want to play with. Having this knowledge, she wants to minimize the number of times she has to hand Johnny a toy from the shelf. Keeping that in mind, she has to put the toys off on the shelf extremely thoughtfully.
TaskWrite a programme that:
reads from the standard input the sequence of toy cars in order in which Johnny will want to play with them,calculates the minimal number of times the mother has to pick cars from the shelf,writes the result to the standard output.
Jasio 是一个三岁的小男孩,他最喜欢玩玩具了,他有n 个不同的玩具,它们都被放在了很高的架子上所以Jasio 拿不到它们. 为了让他的房间有足够的空间,在任何时刻地板上都不会有超过k 个玩具. Jasio 在地板上玩玩具. Jasio'的妈妈则在房间里陪他的儿子. 当Jasio 想玩地板上的其他玩具时,他会自己去拿,如果他想玩的玩具在架子上,他的妈妈则会帮他去拿,当她拿玩具的时候,顺便也会将一个地板上的玩具放上架子使得地板上有足够的空间. 他的妈妈很清楚自己的孩子所以他能够预料到Jasio 想玩些什么玩具. 所以她想尽量的使自己去架子上拿玩具的次数尽量的少,应该怎么安排放玩具的顺序呢?
输入输出格式
输入格式:
In the first line of the standard input there are three integers: nn,kk,pp (1\le k\le n\le 100\ 0001≤k≤n≤100 000, 1\le p\le 500\ 0001≤p≤500 000), separated by single spaces. These denote respectively: the total number of cars, the number of cars that can remain on the floor at once and the length of the sequence of cars which Johnny will want to play with. Each of the following pplines contains one integer. These integers are the numbers of cars Johnny will want to play with (the cars are numbered from 11 to nn).
输出格式:
In the first and only line of the standard output one integer should be written - the minimal number of times his mother has to pick a car from the shelf.
输入输出样例
3 2 7 1 2 3 1 3 1 2
4


/* 贪心,优先队列 首先这个贪心啊,每次删除下次最晚再玩的玩具,要维护next表示下次的位置。然后优先队列。 这样这个玩具这段时间内不会对答案有贡献,且时间最长。 开始想成了每次删除使用总数最少的玩具,发现这个反例大大的有,还不好写。 然后就是代码,问题来自于如何维护已经在队列里的玩具的next 可以每次碰到在队列里的的玩具时把k扩大1,把这个玩具再次放到优先队列。 此时这个玩具的next一定比已经在队列里的这个玩具的next大(好拗口)。 这样就起到了更新next的效果。 */ #include<iostream> #include<cstdio> #include<cstring> #include<queue> #define N 500001 using namespace std; int n,m,k,ans; int cnt[N],c[N],Last[N]; bool vis[N]; struct node{ int num,nxt; friend bool operator < (node x,node y) { return x.nxt<y.nxt; } }a[N]; priority_queue<node>q; int main() { scanf("%d%d%d",&n,&k,&m); for(int i=1;i<=m;i++) scanf("%d",&a[i].num); for(int i=1;i<=n;i++) Last[i]=m+1; for(int i=m;i>=1;i--) a[i].nxt=Last[a[i].num],Last[a[i].num]=i; for(int i=1;i<=m;i++) { if(vis[a[i].num]){k++;q.push(a[i]); continue;} else { if(q.size()==k) { node x=q.top();q.pop(); vis[x.num]=0; } q.push(a[i]); ans++;vis[a[i].num]=1; } } printf("%d\n",ans); return 0; }
1183 泥泞的道路
CS有n个小区,并且任意小区之间都有两条单向道路(a到b,b到a)相连。因为最近下了很多暴雨,很多道路都被淹了,不同的道路泥泞程度不同。小A经过对近期天气和地形的科学分析,绘出了每条道路能顺利通过的时间以及这条路的长度。
现在小A在小区1,他希望能够很顺利地到达目的地小区n,请帮助小明找出一条从小区1出发到达小区n的所有路线中(总路程/总时间)最大的路线。请你告诉他这个值。
第一行包含一个整数n,为小区数。
接下来n*n的矩阵P,其中第i行第j个数表示从小区i到小区j的道路长度为Pi,j。第i行第i个数的元素为0,其余保证为正整数。
接下来n*n的矩阵T,第i行第j个数表示从小区i到小区j需要的时间Ti,j。第i行第i个数的元素为0,其余保证为正整数。
写入一个实数S,为小区1到达n的最大答案,S精确到小数点后3位。
3
0 8 7
9 0 10
5 7 0
0 7 6
6 0 6
6 2 0
2.125
【数据说明】
30%的数据,n<=20
100%的数据,n<=100,p,t<=10000


/* 01分数规划 总路程/总时间=平均速度 可以二分v,建图spfa最长路 判断S总-v*T总=0为最优解,>0当前v满足。 若有正权回路则当前v一定满足(求最长路可以判正环)。 */ #include<iostream> #include<cstdio> #include<cstring> #include<queue> #define N 1001 #define inf 0x3f3f3f3f using namespace std; int n,m,ans,cnt,flag; int s[N][N],t[N][N],in[N]; double dis[N][N],d[N]; bool inq[N]; queue<int>q; void clear() { memset(inq,0,sizeof inq); while(!q.empty()) q.pop(); memset(in,0,sizeof in); for(int i=1;i<=n;i++) d[i]=-inf; } bool spfa(int u) { clear(); q.push(u);inq[u]=1;d[u]=0;in[u]=0; while(!q.empty()) { int now=q.front();q.pop(); inq[now]=0; in[now]++; if(in[now]>=n) return true; for(int i=1;i<=n;i++) { if(i==now) continue; if(d[i]<d[now]+dis[now][i] && s[now][i]) { d[i]=d[now]+dis[now][i]; if(!inq[i]) q.push(i),inq[i]=1; } } }return d[n]>0; } bool check(double x) { for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) dis[i][j]=s[i][j]-t[i][j]*x; return spfa(1); } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",&s[i][j]); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",&t[i][j]); double eps=0.00001,l=0,r=10000; while(r-l>eps) { double mid=(l+r)/2; if(check(mid)) l=mid; else r=mid; } printf("%.3lf\n",l); }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号