清北考前刷题day4早安
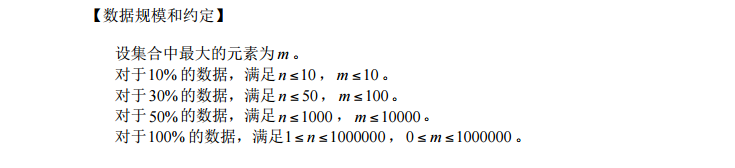

/* 没有考虑次大值有大于一个的情况 */ #include<iostream> #include<cstdio> #include<cstring> #define N 1000007 using namespace std; int n,m,ans,cnt,mx; int a[N]; inline int read() { int x=0,f=1;char c=getchar(); while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int main() { // freopen("multiset.in","r",stdin); // freopen("multiset.out","w",stdout); n=read(); for(int i=1;i<=n;i++) { a[i]=read();mx=max(mx,a[i]); } for(int i=1;i<=n;i++) if(a[i]==mx) cnt++; for(int i=1;i<=n;i++) if((1<<i)>cnt){ans=i;break;} printf("%d\n",ans+mx); return 0; }
/* 扩展不好思考,考虑缩小这些序列。 如果是零就尽量合并,如果非零就都减一。 计数排序O(n) a[0]=(a[0]+1)/2 赋值在a[1]上。 */ #include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 1000010 using namespace std; int n,res,lim; int a[N],cnt[N]; int main() { freopen("multiset.in","r",stdin); freopen("multiset.out","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); lim=max(lim,a[i]); cnt[a[i]]++; } int l=0,z=cnt[0]; for(int i=1;i<=lim;i++) { res++; z=(z+1)/2;z+=cnt[i]; } for(;z>1;z=(z+1)/2)res++; printf("%d",res); return 0; }



#include<cstdio> #include<cstring> const int maxn=1e5+10; const int maxm=5e5+10; inline int min_(int x,int y) { return x<y?x:y; } inline int max_(int x,int y) { return x>y?x:y; } int n,m,l,ans; int t[maxn]; int h[maxn],hs; int et[maxm],en[maxm]; bool v[maxn]; void add() { int u,v; scanf("%d%d",&u,&v); hs++,et[hs]=v,en[hs]=h[u],h[u]=hs; } void dfs(int k,int in,int ax) { if(k==n) { t[ax]=max_(t[ax],in); return; } for(int i=h[k]; i; i=en[i]) if(!v[et[i]]) v[et[i]]=1,dfs(et[i],min_(in,i),max_(ax,i)),v[et[i]]=0; } int main() { freopen("road.in","r",stdin); freopen("road.out","w",stdout); scanf("%d%d",&n,&m); for(int i=1; i<=m; i++) add(); dfs(1,1e9,0); ans=l=1; for(int i=2; i<=m; i++) if(t[i]>=l) { l=i; ans++; } printf("%d\n",ans); return 0; }
/* 考虑这样一个问题:平面上n个点,分成尽量少的点编号连续的点集,使得点集内任意两点的距离不超过一个指定值L。 因为能选尽量选,所以可以考二分下一个断开的位置,但极限数据可以卡掉。 那么这个题我们可以考虑把这个二分变形。 考虑一开始是Start,想找一个start+delta,操作次数尽量小。 有一个办法是delta开始是100,再变成200,300......然后就可以减少二分次数。 最好做法是:delta,1,2,4,8倍增思想。当2^p联通时,2^(p-1)<=delta<=^p。在这个区间内再去做二分。 复杂度sum(O(delta*log))=O(m*log)。 也可以增量法 还是那个模型,但delta->delta+1 vis[i]表示1到i是否可达。多了一条边时,从x->y本来vis[x]=0就不管他,vis[y]=1就不管他。当vis[y]=0 && vis[x]=1才去bfs。 每条边都最多访问一次,总时间复杂度O(m)。 */

#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> #include<cmath> #include<vector> using namespace std; const int N=500010; typedef long long ll; int n, m; int vis[N], u[N], v[N]; vector<int> vec[N]; bool dfs(int u) { if (vis[u]) return false; if (u == n) return true; vis[u] = 1; bool ret = false; for (int i = 0; i < vec[u].size(); i++) { ret = dfs(vec[u][i]); if (ret) return true; } return false; } int read() { char ch = getchar(); int x = 0; while (!isdigit(ch)) ch = getchar(); while (isdigit(ch)) {x = x*10+(ch-'0');ch=getchar();} return x; } bool check(int sta, int las) { for (int i = sta; i <= las; i++) vec[u[i]].push_back(v[i]); bool ret = dfs(1); for (int i = sta; i <= las; i++) { vis[u[i]] = vis[v[i]] = 0; vec[u[i]].clear(); } vis[1] = 0; return ret; } int main() { freopen("road.in","r",stdin); freopen("road.out","w",stdout); n = read(), m = read(); for (int i = 0; i < m; i++) { //scanf("%d%d", &u[i], &v[i]); u[i] = read(); v[i] = read(); } int now = 0, ans = 0; while (now < m) { int i; for (i = 1; i + now <= m; i <<= 1) if (check(now, now + i - 1)) break; i >>= 1; int nowtmp = now + i; for (; i > 0; i >>= 1) if (nowtmp + i <= m && !check(now, nowtmp + i - 1)) nowtmp += i; ans++; now = nowtmp; } cout << ans << endl; }

#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> #include<cmath> #include<vector> using namespace std; const int N=500010; typedef long long ll; int n, m; int vis[N], u[N], v[N]; vector<int> vec[N]; bool dfs(int u) { if (vis[u]) return false; if (u == n) return true; vis[u] = 1; bool ret = false; for (int i = 0; i < vec[u].size(); i++) { ret = dfs(vec[u][i]); if (ret) return true; } return false; } bool check(int sta, int las) { for (int i = sta; i <= las; i++) vec[u[i]].push_back(v[i]); bool ret = dfs(1); for (int i = sta; i <= las; i++) { vis[u[i]] = vis[v[i]] = 0; vec[u[i]].clear(); } vis[1] = 0; return ret; } int main() { freopen("road.in","r",stdin); freopen("road.out","w",stdout); scanf("%d%d", &n, &m); for (int i = 0; i < m; i++) scanf("%d%d", &u[i], &v[i]); int now = 0, ans = 0; while (now < m) { int i; for (i = 1; i + now <= m; i <<= 1) if (check(now, now + i - 1)) break; i >>= 1; int nowtmp = now + i; for (; i > 0; i >>= 1) if (nowtmp + i <= m && !check(now, nowtmp + i - 1)) nowtmp += i; ans++; now = nowtmp; } cout << ans << endl; }


/* 十分贪心 觉得一定是找序列中最小的奇数把它减一最优,如果最小的是偶数,就不管他。 出题人说卡贪心,于是只有十分emmm */ #include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 1007 #define inf 0x3f3f3f3f using namespace std; int n,m,ans,cnt; int a[N]; inline int read() { int x=0,f=1;char c=getchar(); while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int main() { int T;T=read(); while(T--) { n=read();m=n;ans=0; for(int i=1;i<=n;i++) a[i]=read();cnt=0; while(m) { cnt++;sort(a+1,a+n+1); if(cnt&1) { if(a[1]==1)a[1]=inf,ans++,m--; else if(a[1]&1) a[1]--; else continue; } else { for(int i=1;i<=n;i++) { a[i]--; if(a[i]==0) m--,a[i]=inf; } } } printf("%d\n",ans); } }
/* 最理想的情况是1,2,3,4......。可以强行攻击把血量变成这种情况。 但对于有些相同的,就要特殊考虑 比如5,5,5,5,5, 看做1,2,3,4,5 代价就是4,3,2,1,0。 考虑dp。设f[i][j]:考虑到血量为i的兵前面操作中省下了j刀的最大答案。c[i]表示代价。f[i][j[=max(f[i-1][j-1],f[i-1][j+c[i]]+1)。据说是背包dp模型。 对于c的处理可以计数排序。 但有一个问题,2,4,5,5时 5->1而不是3。用栈维护。 */ #include <iostream> #include <cstdio> #include <cstdlib> #include <algorithm> #include <cmath> #include <cstring> using namespace std; const int MAXN = 1000 + 10; int a[MAXN]; int cnt[MAXN], sta[MAXN], c[MAXN]; int f[MAXN][MAXN]; int main() { freopen("cs.in", "r", stdin); freopen("cs.out", "w", stdout); int T; scanf("%d", &T); for (int num = 1; num <= T; ++num) { int N, maxn = 0; scanf("%d", &N); memset(cnt, 0, sizeof(cnt)); memset(c, 0, sizeof(c)); memset(f, 0, sizeof(f)); for (int i = 1; i <= N; ++i) { scanf("%d", &a[i]); ++cnt[a[i]]; maxn = max(maxn, a[i]); } int top = 0; for (int i = 1; i <= maxn; ++i) if (cnt[i] == 0) sta[++top] = i; else { while (cnt[i] > 1 && top > 0) {c[sta[top--]] = i; --cnt[i];} c[i] = i; } int ans = 0; for (int i = 1; i <= maxn; ++i) for (int j = 0; j <= i; ++j) { if (j > 0) f[i][j] = f[i - 1][j - 1]; if (c[i] != 0 && j + c[i] - i < i) f[i][j] = max(f[i][j], f[i - 1][j + c[i] - i] + 1); ans = max(ans, f[i][j]); } printf("%d\n", ans); } return 0; }
折花枝,恨花枝,准拟花开人共卮,开时人去时。
怕相思,已相思,轮到相思没处辞,眉间露一丝。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号