湖南集训day8

 

难度:☆☆☆☆☆☆☆

 

 

 

 

/*
可以先考虑一维，可知 模k意义下相同的前缀和任意两个相减都是k的倍数
问题等价于统计前缀何种模k相同的数的对数。
多维的时候二维前缀和,压行或者压列，n^3可以解决。 
*/
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define K 1000007
#define N 400

using namespace std;
typedef long long LL;
int f[K],s[N][N];

int main()
{
    freopen("rally.in", "r", stdin);
    freopen("rally.out", "w", stdout);
    int n,m,k;
    scanf("%d%d%d",&n,&m,&k);
    for (int i=1;i<=n;i++)
        for (int j=1;j<=m;j++)
        {
            scanf("%d",s[i]+j);
            s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
            if (s[i][j]<0) s[i][j]+=k;
            if (s[i][j]>0) s[i][j]%=k;
        }
    LL ans=0;
    f[0]=1;
    for (int l=1;l<=m;l++)
        for (int r=l;r<=m;r++)
        {
            for (int i=1;i<= n;i++)
            {
                int sum=s[i][r]-s[i][l-1];
                if (sum<0) sum+=k;
                ans+=f[sum];f[sum]++;
            }
            for (int i=1;i<=n;i++)
            {
                int sum=s[i][r]-s[i][l-1];
                if (sum<0) sum+=k;f[sum]--;
            }
        }
    printf("%lld\n",ans);
    return 0;
}

 

 

/*
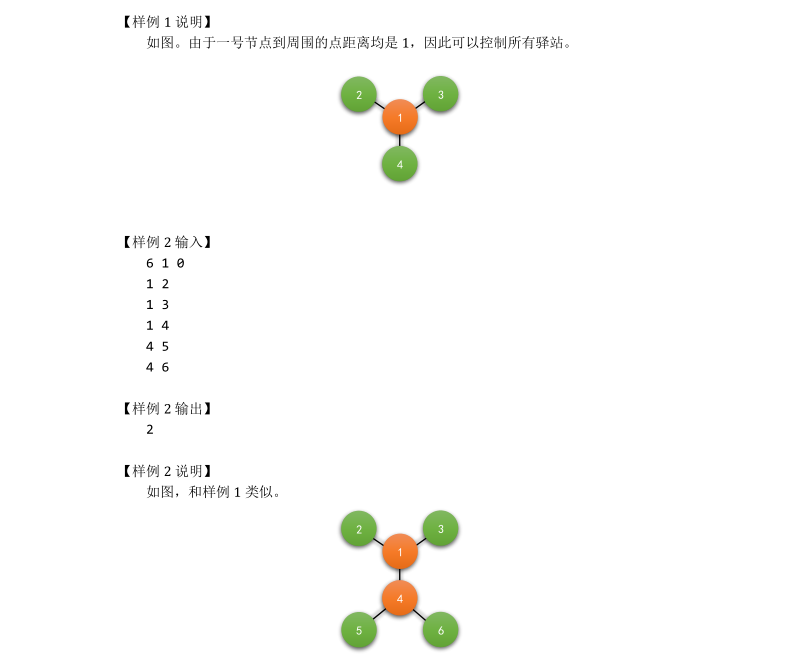
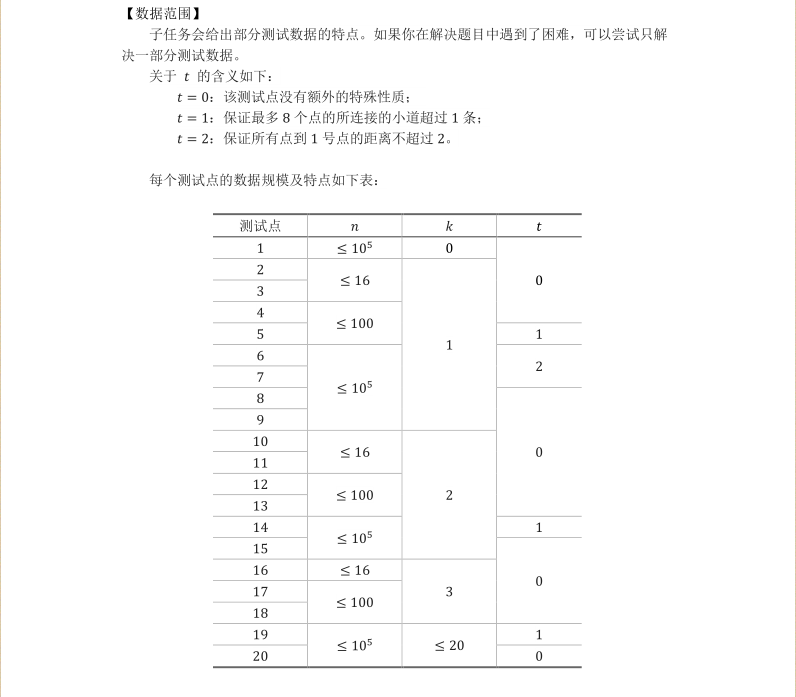
树形dp可做，好难好难的样子
考虑贪心 暗点的深度排序，每次拿出未被更新的最深的点把他的k级父亲标记 
然后用这个点向外扩展更新每个点距离标记点的距离 
正确性显然 
*/
#include<iostream>
#include<cstdio>
#include<cstring>

#define N 100007

using namespace std;
int head[N],q[N],f[N],fa[N];
int n,m,ans,cnt,K,t;
struct edge{
    int u,v,net;
}e[N<<1];

inline int read()
{
    int x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

inline void add(int u,int v)
{
    e[++cnt].v=v;e[cnt].net=head[u];head[u]=cnt;
}

void bfs()
{
    int he=1,ta=1;
    q[ta++]=1;fa[1]=1;
    while(he<=ta)
    {
        int u=q[he++];;
        for(int i=head[u];i;i=e[i].net)
        {
            int v=e[i].v;
            if(!fa[v])
            {
                fa[v]=u;q[ta++]=v;
            } 
        }
    }
}

void update(int u)
{
    if(!f[u]) return;
    for(int i=head[u];i;i=e[i].net)
    {
        int v=e[i].v;
        if(f[v]<f[u]-1)
          f[v]=f[u]-1,update(v);
    }
}

int main()
{
    freopen("general.in", "r", stdin);
    freopen("general.out", "w", stdout);
    int x,y;
    n=read();K=read();t=read();
    for(int i=1;i<n;i++)
    {
        x=read();y=read();
        add(x,y);add(y,x);
    }
    bfs();
    memset(f,-1,sizeof f);
    for(int i=n;i;i--)
    {
        if(f[q[i]]==-1)
        {
            int j=q[i];
            for(int k=K;k;k--) j=fa[j];
            ans++;f[j]=K;
            update(j);
        }
    }
    printf("%d\n",ans);
    return 0;
}

 

 

 

这道题简直了，妙不可言！！！！！！！！！！！！！！

前方高能题解

 

 

 

可是...那个“比较简单的状压dp”怎么写啊......

gg

 

std

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> pii;
#define fir first
#define sec second
#define INF 0x3f3f3f3f
#define MAXN 40005
#define TOP 18

int n, K, m, cnt = 0;
bool a[MAXN];
int dis[18][MAXN], b[70];
pii p[18];

queue <int> q;

void bfs(pii st)
{
	for (int i = 0; i < MAXN; i++) dis[st.fir][i] = INF;
	q.push(st.sec);
	dis[st.fir][st.sec] = 0;
	while (!q.empty())
	{
		int x = q.front();
		q.pop();
		for (int i = 1; i <= m; i++)
		{
			if (x - b[i] >= 0 && dis[st.fir][x - b[i]] > dis[st.fir][x] + 1)
			{
				dis[st.fir][x - b[i]] = dis[st.fir][x] + 1;
				q.push(x - b[i]);
			}
			if (x + b[i] <= n && dis[st.fir][x + b[i]] > dis[st.fir][x] + 1)
			{
				dis[st.fir][x + b[i]] = dis[st.fir][x] + 1;
				q.push(x + b[i]);
			}
		}
	}
}

int dp[1 << 18];

int solve(int mask)
{
	if (dp[mask] != -1) return dp[mask];
	if (mask == 0) return 0;
	int &ret = dp[mask];
	ret = INF;
	int x = 0;
	while (!(mask & (1 << x))) x++;
	for (int i = x + 1; i < 2 * K; i++)
		if (mask & (1 << i)) ret = min(ret, solve(mask ^ (1 << x) ^ (1 << i)) + dis[x][p[i].sec]);
	return ret;
}

int main()
{
	freopen("starlit.in", "r", stdin);
	freopen("starlit.out", "w", stdout);
	scanf("%d %d %d", &n, &K, &m);
	for (int i = 1, x; i <= K; i++) scanf("%d", &x), a[x] = true;
	for (int i = 1; i <= m; i++) scanf("%d", &b[i]);
	for (int i = 0; i <= n; i++) if (a[i] != a[i + 1]) p[cnt] = pii(cnt, i), cnt++;
	for (int i = 0; i < cnt; i++) bfs(p[i]);
	memset(dp, -1, sizeof dp);
	int ans = solve((1 << cnt) - 1);
	assert(ans != INF);
	printf("%d\n", ans);
	return 0;
}