洛谷P1731生日蛋糕(dfs+剪枝)

 P1731 生日蛋糕

题目背景

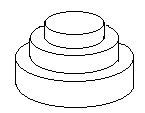
7月17日是Mr.W的生日，ACM-THU为此要制作一个体积为Nπ的M层

生日蛋糕，每层都是一个圆柱体。

设从下往上数第i(1<=i<=M)层蛋糕是半径为Ri, 高度为Hi的圆柱。当i<M时，要求Ri>Ri+1且Hi>Hi+1。

由于要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积Q最小。

令Q= Sπ

请编程对给出的N和M，找出蛋糕的制作方案（适当的Ri和Hi的值），使S最小。

（除Q外，以上所有数据皆为正整数）

题目描述

输入输出格式

输入格式：

 

有两行，第一行为N（N<=20000），表示待制作的蛋糕的体积为Nπ；第二行为M(M<=15)，表示蛋糕的层数为M。

 

输出格式：

 

仅一行，是一个正整数S（若无解则S=0）。

 

输入输出样例

输入样例#1：

100
2

输出样例#1：

68

/*
①要是剩下体积除以最大(虽然取不到)半径所得到的表面积+累计表面积大于答案退出
② 要是剩下来的体积已经小于该层最小体积了就退出
③ 还有 为了剪枝,我们要起先预处理某一层的最大不可的表面积和体积
*/
#include<cstdio>
#include<cmath>
#include<algorithm>

#define maxn 17

using namespace std;
int NN,M,N,ans;
int ss[maxn],sv[maxn];

void dfs(int t,int S,int V,int lR,int lH)//层数，已用总面积，已用总体积，上一层半径 ，上一层高度
{
    if (t==0)
    {
        if (V==N) ans=min(ans,S);
        return ;
    }
    if (V+sv[t]>N) return;
    if (S+ss[t]>ans) return;
    if (S+2*(N-V)/lR>ans) return;
    for (int r=lR-1;r>=t;r--)
    {
        if (t==M) S=r*r;
        int maxh=min((N-V-sv[t-1])/(r*r),lH-1);
        for (int h=maxh;h>=t;h--)
          dfs(t-1,S+2*r*h,V+r*r*h,r,h);
    }
}

int main()
{
    scanf("%d%d",&N,&M);
    for (int i=1;i<=M;i++)
    {
        ss[i]=2*i*i;ss[i]+=ss[i-1];
        sv[i]=i*i*i;sv[i]+=sv[i-1];
    }ans=0x3f3f3f3f;
    dfs(M,0,0,sqrt(N),N);
    if (ans==0x3f3f3f3f) printf("0");
    else printf("%d\n",ans);
    return 0;
}