9.11NOIP模拟题
NOIP模拟赛
by thmyl
|
题目名称 |
superman |
market |
Lemon_Soda |
|
可执行文件名 |
superman |
market |
Lemon_Soda |
|
输入文件 |
superman.in |
market.in |
Lemon_Soda.in |
|
输出文件 |
superman.out |
market.out |
Lemon_Soda.out |
|
时间限制 |
1s |
1s |
1s |
|
是否有部分分 |
无 |
无 |
无 |
|
满分 |
100 |
100 |
100 |
|
空间限制 |
250M |
128M |
128M |
|
测试点数量 |
5 |
10 |
10 |
Problem 1. superman
【题目描述】
小可乐是要登上世界顶峰的男人!为了向他的妹子证明自己的能力,他决定去撒哈拉沙漠找到依米花送给他的妹子。
假设途中经过N个地区,编号为1~N,小可乐一开始在编号为1的地区,编号为N的地区代表撒哈拉沙漠,地区之间由于地形差别悬殊,并不是都可以直连的。同时由于不同经度存在时差,小可乐看了当地的地方时会以为出现了时间静止甚至倒流,所以我们假设两地区之间的穿行时间可以是负数或0,另外,由地区i到地区j的时间和由地区j到地区i的时间不一定是相同的。
小可乐在非洲的网友DDL被他感动了,决定去城市n迎接小可乐的到来,小可乐可以自己调整行动速度,为了不让DDL等得太着急,他想调整自己行动的速度,使得在每一条路上花费的时间都加或减一个整数,你的任务是调整小可乐的行动速度,找出一条用最短时间到达地区N的路径,并且保证这个最短时间的值大于或等于0。
【输入格式】
输入文件包含多组数据,第1个数为T,表示数据的数量。
对于每一组数据,输入第1行为两个正整数N,E,为地区的个数和地区间的路线数。然后E行,每行三个整数i,j和t(1≤i,j≤N,i≠j),表示由地区i到地区j穿行的时间为t。由i到j最多只会有一条穿行线路。
【输出格式】
输出文件共T行,每组数据输出一行;
如果可以通过调节速度到达地区N,则输出一个非负整数,表示由地区1到地区N的最短时间。
如果不能由地区1到达地区N,则输出-1。
【输入样例】
1
4 5
1 2 1
1 3 1
2 3 -3
3 1 1
3 4 1
【输出样例】
2
【样例说明】
输入样例如图所示,其中节点标号表示相应地区,节点间数字表示所需时间。
如果设置控制速度的值为0,则有如下路径:1→2→3→1→2→……→3→4,使得投递的时间为负无穷大,显然是不符合要求的,所以应该把控制速度的值设为1,相当于每个时间值加1,得到的最短路径为1→2→3→4,所需时间为2+(-2)+2=2。
/* 因为与n不连通的负环对答案无影响 所以先floyd预处理连通性 二分每条边上增加的数量,然后spfa判断 判断的时候必须edge[i].to能连到n才可以进队列 入队列n次说明有负环,当前答案不可行。 */ #include<iostream> #include<cstdio> #include<cstring> #include<queue> #define N 101 using namespace std; int head[N],vis[N],d[N],p[N]; int can[N][N]; int n,m,ans,cnt,num; queue<int>q; struct node { int u,v,net,dis; }e[N<<1]; inline int read() { int x=0,f=1;char c=getchar(); while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } void init() { memset(head,0,sizeof head); memset(p,0,sizeof p); memset(vis,0,sizeof vis); memset(can,0,sizeof can); for(int i=1;i<=n;i++) can[i][i]=1; cnt=0;while(!q.empty()) q.pop(); } inline void add(int u,int v,int dis) { e[++cnt].v=v;e[cnt].net=head[u];e[cnt].dis=dis;head[u]=cnt; } void dfs(int now) { vis[now]=1; for(int i=head[now];i;i=e[i].net) { int v=e[i].v; if(vis[v])continue; vis[v]=1; dfs(v); }return; } void floyd() { for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(can[i][k] && can[k][j]) can[i][j]=1; } bool spfa(int now) { memset(d,127,sizeof d); memset(vis,0,sizeof vis); memset(p,0,sizeof p); d[now]=0;vis[now]=1;q.push(now); while(!q.empty()) { int u=q.front();q.pop();vis[u]=0; for(int i=head[u];i;i=e[i].net) { int v=e[i].v; if(d[v]>d[u]+e[i].dis && can[v][n]) { d[v]=d[u]+e[i].dis; if(!vis[v]) { vis[v]=1; q.push(v); if(++p[v]>n) return false; } } } } if(d[n]<0) return false; return true; } bool AD(int k) { for(int i=1;i<=m;i++) e[i].dis+=k; bool res=spfa(1); for(int i=1;i<=m;i++) e[i].dis-=k; return res; } int main() { int x,y,T,z; T=read(); while(T--) { n=read();m=read();init(); for(int i=1;i<=m;i++) { x=read();y=read();z=read(); can[x][y]=1; add(x,y,z); } dfs(1); if(!vis[n]) printf("-1\n"); else { floyd(); int l=-200000,r=200000; while(l<=r) { int mid=(l+r)>>1; if(AD(mid)) r=mid-1,ans=mid; else l=mid+1; }AD(ans); printf("%d\n",d[n]); } } return 0; }
Problem 2. market
【题目描述】
小可乐的妹子不在家,他只好自己去逛超市,小可乐最喜欢喝汽水,买到汽水会使小可乐开心起来,但是他也不愿意看到手里的毛毛变少,所以每买一瓶汽水也会有点难过,很显然他又遇到了很多麻烦。
现在小可乐面前有n瓶汽水,编号分别为1,2,3,……,n。他可以在这当中任意选择任意多瓶。其中第i瓶汽水有两个属性Wi和Ri,当他选择了第i瓶汽水后,就可以获得Wi的开心值;但是,他选择该汽水以后选择的所有汽水的开心值都会减少Ri。现在请你求出,该选择哪些汽水,并且该以什么样的顺序选取这些汽水,才能使得小可乐获得的开心值最大。
注意,开心值的减少是会叠加的。比如,选择了第i瓶汽水,那么就会获得Wi的开心值;然后又选择第j瓶汽水,又会获得了Wj-Ri开心值;之后又选择第k瓶汽水,又会获得Wk-Ri-Rj的开心值;那么他获得的开心值总和为Wi+(Wj-Ri)+(Wk-Ri-Rj)。
【输入格式】
第一行一个正整数n,表示汽水的瓶数。
接下来第2行到第n+1行,每行两个正整数Wi和Ri,含义如题目所述。
【输出格式】
输出仅一行,表示最大的开心值。
【输入样例】
2
5 2
3 5
【输出样例】
6
【说明】
20%的数据满足:n<=5,0<=Wi,Ri<=1000。
50%的数据满足:n<=15,0<=Wi,Ri<=1000。
100%的数据满足:n<=3000,0<=Wi,Ri<=200000。
样例解释:我们可以选择第1瓶汽水,获得了5点开心值;之后我们再选择第2瓶汽水,获得3-2=1点开心值。最后总的开心值为5+1=6。
/* 首先仍然是要按照Ri从大到小排个序。然后设F[i][j]表示前i个物品中选j个可以获得的收益最大值。 状态转移方程:F[i][j]=max{F[i-1][j],F[i-1][j-1]+W[i]-R[i]*(j-1)} 边界条件:F[1][1]=W[1] 最后的答案=max{F[n][i]} */ #include<iostream> #include<cstdio> #include<algorithm> #define N 3010 using namespace std; int ans,n,dp[N][N]; struct node { int w,r; }a[N]; int cmp(node x,node y){return x.r>y.r;} int main() { scanf("%d",&n); for(int i=1;i<=n;i++)scanf("%d%d",&a[i].w,&a[i].r); sort(a+1,a+n+1,cmp); dp[1][1]=a[1].w; for(int i=2;i<=n;i++) for(int j=1;j<=i;j++) dp[i][j]=max(dp[i][j],max(dp[i-1][j],dp[i-1][j-1]+a[i].w-a[i].r*(j-1))); for(int i=1;i<=n;i++) ans=max(ans,dp[n][i]); printf("%d",ans); fclose(stdin);fclose(stdout); return 0; }
Problem 3. Lemon_Soda
【题目描述】
小可乐惊喜的发现一瓶汽水中了再来一瓶,他去商店换汽水的时候,店主Lemon和Soda打算耍耍他,出了一个难题,而且做不出来就不给汽水喝
这题说的是:
使得 达到或超过 n 位数字的最小正整数 x 是多少?
小可乐见了两位妹子紧张的不敢说话,快请你帮帮他解决这个难题吧
【输入格式】
一个正整数 n
【输出格式】
使得 达到 n 位数字的最小正整数 x
【输入样例】
11
【输出样例】
10
【说明】
n<=2000000000
换底公式
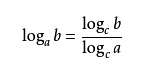
/* 看到如此之大的数据范围,显然强行计算x^x的位数是不现实的,不仅需要高精度,而且效率极低。 题目的核心在于如何计算x^x的位数,可以利用对数的方法,log10(x)就是x的位数。 也就是 log10(x^x)>=n-1 如此判定方法就是简单了,代码形式就是 x * log(x) / log(10)(换底公式) >= n - 1 求最小,很明显是二分搜索,二分套一个判断函数就完成了此题。 */ #include<iostream> #include<cstdio> #include<cstring> #include<cstdlib> #include<cmath> #define N 1000000000 using namespace std; bool judge(long long x, int n) { return x*(log(x)/log(10))>=n-1; } void BC(int l, int r, int n) { int ans; while(l<=r) { int mid=(l + r)>>1; bool cur=judge(1ll*mid,n); if(cur)r=mid-1,ans=mid; else l=mid+1; } printf("%d\n",ans); return; } int main() { int n; scanf("%d", &n); BC(0,N,n); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号