扩展欧几里得

 

1.poj1601 http://poj.org/problem?id=1061

                                                                                                                  青蛙的约会
 
Time Limit: 1000MS   Memory Limit: 10000K
Total Submissions: 113835   Accepted: 23262

Description

两只青蛙在网上相识了，它们聊得很开心，于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上，于是它们约定各自朝西跳，直到碰面为止。可是它们出发之前忘记了一件很重要的事情，既没有问清楚对方的特征，也没有约定见面的具体位置。不过青蛙们都是很乐观的，它们觉得只要一直朝着某个方向跳下去，总能碰到对方的。但是除非这两只青蛙在同一时间跳到同一点上，不然是永远都不可能碰面的。为了帮助这两只乐观的青蛙，你被要求写一个程序来判断这两只青蛙是否能够碰面，会在什么时候碰面。 
我们把这两只青蛙分别叫做青蛙A和青蛙B，并且规定纬度线上东经0度处为原点，由东往西为正方向，单位长度1米，这样我们就得到了一条首尾相接的数轴。设青蛙A的出发点坐标是x，青蛙B的出发点坐标是y。青蛙A一次能跳m米，青蛙B一次能跳n米，两只青蛙跳一次所花费的时间相同。纬度线总长L米。现在要你求出它们跳了几次以后才会碰面。 

Input

输入只包括一行5个整数x，y，m，n，L，其中x≠y < 2000000000，0 < m、n < 2000000000，0 < L < 2100000000。

Output

输出碰面所需要的跳跃次数，如果永远不可能碰面则输出一行"Impossible"

Sample Input

1 2 3 4 5

Sample Output

4

/*
扩展欧几里得应用
(x+m*t)-(y+n*t)=p*L (t是跳的次数，p是a,b的圈数差)
等价于:(n-m)*t+L*p=y-x;
令a=n-m;b=L;c=y-x;
等价于:a*t+b*p=c;
求t的最小整数解。

用扩展欧几里得求出其中一组解t0,p0,令g=gcd(a,b);
因为不定方程有解,所以a*t/g  b*t/g  d/g 为整数
方程两边都乘(c/g) 得到 a*t0*(c/g)+b*p0*(c/g)=c*(c/g);
所以 t0*(c/g)是最小解.但有可能是负数
因为 a*(t0*(c/g)+b*k)+b*(p0*(c/g)-a*k)=c*(c/g);其中k是自然数 
所以解为 (t0*(c/g)%b+b)%b;
*/


#include<iostream>
#include<cstdio>
#include<cmath>

using namespace std;
long long a,b,c,m,n,l,x,y,g;

void ex_gcd(long long a,long long b)//求出一组解t0,p0 
{
    if(b==0)
    {
        x=1;y=0;g=a;
        return;
    }
    ex_gcd(b,a%b);
    long long tmp=x;x=y;y=tmp-a/b*y;
}

int main()
{
    scanf("%lld%lld%lld%lld%lld",&x,&y,&m,&n,&l);
    a=m-n;b=l;c=y-x;
    if(a<0){a=-a;c=-c;}
    ex_gcd(a,b);
    if(c%g){printf("Impossible\n");return 0;}//无解 
    else//有解 
    {
        x=x*c/g;l=l/g;
        x=(x%l+l)%l;//处理x可能为负 
        printf("%d\n",x);
    }
    return 0;
}

 2.hdu 1576 http://acm.hdu.edu.cn/showproblem.php?pid=1576

A/B

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 5595    Accepted Submission(s): 4369


Problem Description
要求(A/B)%9973，但由于A很大，我们只给出n(n=A%9973)(我们给定的A必能被B整除，且gcd(B,9973) = 1)。
 

 

Input
数据的第一行是一个T，表示有T组数据。
每组数据有两个数n(0 <= n < 9973)和B(1 <= B <= 10^9)。
 

 

Output
对应每组数据输出(A/B)%9973。
 

 

Sample Input
2 1000 53 87 123456789
 

 

Sample Output
7922 6060
 
/*
给出了n=A%9973 和B
考虑用ex_gcd
n=A%9973,则n=A-A/9973*9973。
又A/B=x,则A=Bx。所以Bx-A/9973*9973=n。即Bx-9973y=n.
到这里我们可以发现:只要求出x的值,就可算出x%9973,也就是(A/B)%9973了.
用扩展欧几里德算法可求出gcd(B,9973)=Bx1+9973y1=1的x1。
等式两边同乘以n，得B(nx1)-9973(-ny1)=n。
可知nx1就是Bx-9973y=n的解了,即x=nx1。x可能是负数，处理一下。 
*/ 
#include<iostream>
#include<cstdio>
#include<cstring>
#define mod 9973

using namespace std;
int n,A,B,g,x,y;

void exgcd(int a,int b)
{
    if(b==0)
    {
        x=1;y=0;g=a;
        return;
    }
    exgcd(b,a%b);
    int tmp=x;x=y;y=tmp-a/b*y;
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&B);
        exgcd(B,mod);
        x=(x%mod+mod)%mod;
        printf("%d\n",(x*n)%mod);        
    }
    return 0;
}

 3.poj2142 http://poj.org/problem?id=2142

The Balance
Time Limit: 5000MS   Memory Limit: 65536K
Total Submissions: 6620   Accepted: 2912

Description

Ms. Iyo Kiffa-Australis has a balance and only two kinds of weights to measure a dose of medicine. For example, to measure 200mg of aspirin using 300mg weights and 700mg weights, she can put one 700mg weight on the side of the medicine and three 300mg weights on the opposite side (Figure 1). Although she could put four 300mg weights on the medicine side and two 700mg weights on the other (Figure 2), she would not choose this solution because it is less convenient to use more weights. 
You are asked to help her by calculating how many weights are required. 

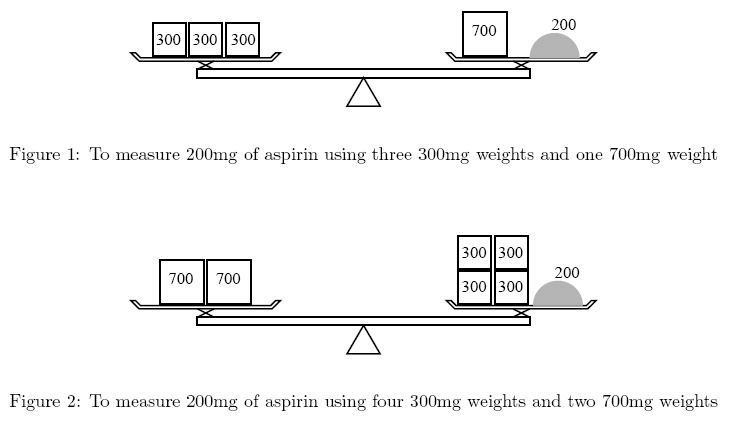
Input

The input is a sequence of datasets. A dataset is a line containing three positive integers a, b, and d separated by a space. The following relations hold: a != b, a <= 10000, b <= 10000, and d <= 50000. You may assume that it is possible to measure d mg using a combination of a mg and b mg weights. In other words, you need not consider "no solution" cases. 
The end of the input is indicated by a line containing three zeros separated by a space. It is not a dataset.

Output

The output should be composed of lines, each corresponding to an input dataset (a, b, d). An output line should contain two nonnegative integers x and y separated by a space. They should satisfy the following three conditions. 
  • You can measure dmg using x many amg weights and y many bmg weights. 
  • The total number of weights (x + y) is the smallest among those pairs of nonnegative integers satisfying the previous condition. 
  • The total mass of weights (ax + by) is the smallest among those pairs of nonnegative integers satisfying the previous two conditions.

No extra characters (e.g. extra spaces) should appear in the output.

Sample Input

700 300 200
500 200 300
500 200 500
275 110 330
275 110 385
648 375 4002
3 1 10000
0 0 0

Sample Output

1 3
1 1
1 0
0 3
1 1
49 74
3333 1
/*
题意：一个家伙有一种天平，这种天平只有两种重量的砝码a和b，
现在要称出重量为c的物品，问你至少需要多少a和b，答案需要满足a的数量加上b的数量和最小，
并且他们的重量和也要最小。（两个盘都可以放砝码）
输入 物品 a b 
输出 a b 个数 

好题！ 
应该满足ax+by==c。x,y为正时表示放在和c物品的另一边，为负时表示放在c物品的同一边。
根据通解:|x|+|y|==|x0+b/d*t|+|y0-a/d*t| 规定a>b
可以看出|x0+b/d*t|是单调递增的，|y0-a/d*t|是单调递减的 
而由于我们规定了a>b，那么减的斜率边要大于增的斜率，于是整个函数减少的要比增加的快
但是由于绝对值的符号的作用，最终函数还是递增的。
很显然是y0-a/d*t==0的时候最小 于是我们的最小值|x|+|y|也一定是在t=y0*d/a附近了
我枚举了10个数。 
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdio>

using namespace std;
int a,b,c,g,x,y;

int wokao(int a)//abs 不过编！！！wokao！！！！ 
{
    if(a<0)return -a;
    else return a;
}

int exgcd(int a,int b)
{
    if(b==0)
    {
        x=1;y=0;
        return a;
    }
    g=exgcd(b,a%b);
    int tmp=x;x=y;y=tmp-a/b*y;
    return g;
}

int main()
{
    int x1,x2,y1,y2;
    while((scanf("%d%d%d",&a,&b,&c))==3)
    {
        if(!a&& !b&& !c) break;
        int flag=0;
        if(a<b) swap(a,b),flag=1;
        g=exgcd(a,b);
        x=x*c/g;y=y*c/g;//这个地方原来不是很明白
        //ax+by=c  exgcd中 x,y是求得关于gca(a,b)的解，应该是求关于c的解，所以要变回去 
        int t=y*g/a,ans=0x3f3f3f3f;//y=y0-(a/g)*t  y==0 —> t=y0*g/a; 
//        while(y-a*t<0) t--;
        for(int i=t-5;i<=t+5;i++)
        {
            x2=x+(b/g)*i;
            y2=y-(a/g)*i;
            if(wokao(x2)+wokao(y2)<ans)
            {
                ans=wokao(x2)+wokao(y2);
                x1=x2;
                y1=y2;
            }
        }
        if(!flag) printf("%d %d\n",wokao(x1),wokao(y1));
        else printf("%d %d\n",wokao(y1),wokao(x1));
    }
    return 0;
}

 

COGS2057 殉国  http://cogs.pro/cogs/problem/problem.php?pid=2057

2057. [ZLXOI2015]殉国

★☆   输入文件：BlackHawk.in   输出文件：BlackHawk.out   评测插件
时间限制：0.05 s   内存限制：256 MB

【题目描述】

 


正义的萌军瞄准了位于南极洲的心灵控制器，为此我们打算用空袭摧毁心灵控制器，然而心灵控制器是如此强大，甚至能缓慢控制飞行员。一群勇敢的士（feng）兵（zi）决定投弹后自杀来避免心灵控制。然而自杀非常痛苦，所以萌军指挥官决定到达目的地后让飞机没油而坠落(也避免逃兵)。军官提供两种油：石油和中国输送来的地沟油,刚开始飞机没有油，飞机可以加几桶石油和几桶地沟油(假设石油和地沟油都有无限桶)，飞机落地时必须把油耗尽，已知一桶石油和一桶地沟油所能支撑的飞行距离分别为a,b,驾驶员们必须飞往一个目的地，总距离为c.

1.最少，最多需要加几桶油，若只有一种方案，最少和最多的是相同的.

2.总共有多少种不同的加油配方(死法)能到达目的地。

【输入格式】

只有一行，三个正整数a,b,c

【输出格式】

两行，第一行为最少加几次油和最多加几次油，

第二行为加油方法总数。

若不存在任何方法，第一行输出-1 -1

第二行输出0

【样例输入】

样例1：
2 3 10
样例2：
6 8 10

【样例输出】

样例1：
4 5
2
样例2：
-1 -1
0

【提示】

样例解释：

样例一：飞机加两次石油，两次地沟油，总次数为4，2*2+3*3=10

飞机加五次石油，不加地沟油，总次数为5,2*5+3*0=10

总共两种

样例二：飞机无法到达目的地

数据范围：

对于10%的数据,a<=103,b<=103,c<=103

对于20%的数据,a<=104,b<=104,c<=106

对于50%的数据，a<=109，b<=109,c<=109

对于100%数据，a<=3⋅1018，b<=3⋅1018,c<=3⋅1018

三个答案分值权重分别为20%,30%,50%

 

/*
题目大意：Ax+By=C,x>=0,y>=0,求x+y最大值，x+y最小值
x,y的解得个数
暴力算法1：枚举x,y更新O(N^2)20分
暴力算法2：枚举x，测试y是否符合情况，O(N) 40分-100分（原谅我数据太水）
很明显的扩展欧几里得
令gcd(A,B)=D;
Ax+By=C满足有解的必要条件是C mod D = 0
我们先解方程Ax+By=gcd(A,B),得到该方程一组解(p',q’)乘以C/D
即为原方程的一组解(p0,q0)
则任何(p,q)满足
p = p0 +B/D *t
q = q0–A/D *t(其中t为任意整数)都为原方程的解
我们解不等式p>=0&&q>=0得到关于t的一个区间[l,r]
(注意不等式的向下取整和向上取整)
则通解个数显然为r-l+1
最小最大解一定分别在l,r处取得（因为是线性方程）
时间复杂度O(logN)
*/

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>

#define LL long long 

using namespace std;
LL a,b,c,x,y;

LL gcd(LL a,LL b)
{
    if(b==0)return a;
    else return gcd(b,a%b);
}
LL exgcd(LL a,LL b,LL &x ,LL & y)
{
    if(b==0)
    {x=1;y=0;return a;}
    LL r=exgcd(b,a%b,x,y);
    LL tmp=x;x=y;y=tmp-(a/b)*y;
    return r;
}
int main()
{
    //freopen("BlackHawk.in","r",stdin);
    //freopen("BlackHawk.out","w",stdout);
    cin>>a>>b>>c;
    LL p=gcd(a,b);
    if(c%p!=0)
    {
        printf("-1 -1\n0");
        return 0;
    }
    exgcd(a,b,x,y);
    LL xx=ceil((long double)-x/b*c);
    LL yy=floor((long double)y/a*c);
    LL ans=yy-xx+1;
    LL ans1=x*c/p+y*c/p+(b-a)/p*yy;
    LL ans2=x*c/p+y*c/p+(b-a)/p*xx;
    if(ans<=0) printf("-1 -1\n0");
    else cout<<min(ans1,ans2)<<" "<<max(ans1,ans2)<<endl<<ans;
    return 0;
}

 

posted @ 2017-04-22 17:37  安月冷  阅读(241)  评论(0)  编辑  收藏  举报