洛谷P2668斗地主（搜索）noip2015

题目描述

牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中，牌的大小关系根据牌的数码表示如下：3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。

现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。

需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。

具体规则如下：

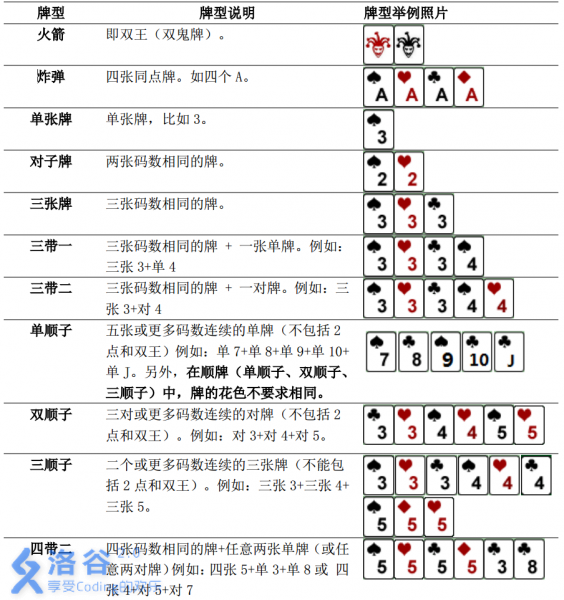
输入输出格式

输入格式：

 

第一行包含用空格隔开的2个正整数T和n，表示手牌的组数以及每组手牌的张数。

接下来T组数据，每组数据n行，每行一个非负整数对aibi表示一张牌，其中ai示牌的数码，bi表示牌的花色，中间用空格隔开。特别的，我们用1来表示数码A，11表示数码J，12表示数码Q，13表示数码K；黑桃、红心、梅花、方片分别用1-4来表示；小王的表示方法为01，大王的表示方法为02。

 

输出格式：

 

共T行，每行一个整数，表示打光第i手牌的最少次数。

 

输入输出样例

输入样例#1：

1 8
7 4
8 4
9 1
10 4
11 1
5 1
1 4
1 1

输出样例#1：

3

输入样例#2：

1 17
12 3
4 3
2 3
5 4
10 2
3 3
12 2
0 1
1 3
10 1
6 2
12 1
11 3
5 2
12 4
2 2
7 2

输出样例#2：

6

说明

样例1说明

共有1组手牌，包含8张牌：方片7，方片8，黑桃9，方片10，黑桃J，黑桃5，方片A以及黑桃A。可以通过打单顺子（方片7，方片8，黑桃9，方片10，黑桃J），单张牌（黑桃5）以及对子牌（黑桃A以及方片A）在3次内打光。

对于不同的测试点， 我们约定手牌组数T与张数n的规模如下：

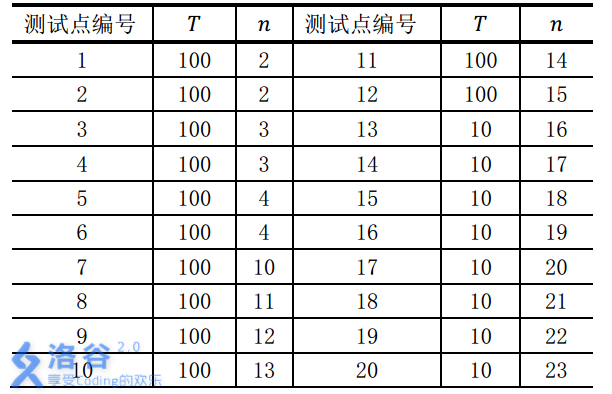
数据保证：所有的手牌都是随机生成的。

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;
int x[10],y[10],z[10],k[10],num[200];
int T,cnt,flag,n;

bool cmp(int a,int b)
{
    return a>b;
}

int main()
{
    scanf("%d%d",&T,&n);
    while(T--)
    {
        flag=0,cnt=0;
        memset(z,0,sizeof z);
        memset(x,0,sizeof x);
        memset(num,0,sizeof num);
        if(n>4) return 0;
        for(int i=1;i<=n;i++)
        {
            scanf("%d%d",&x[i],&y[i]);
            num[x[i]]++;
        }
        for(int i=0;i<=25;i++)
        {
            if(num[i]!=0)
              z[++cnt]=num[i];
        }
        sort(z+1,z+n+1,cmp);
        if(z[1]==1)
        {
            cout<<n<<endl;
            continue;
        }
        if(z[1]==n)
        {
            cout<<"1"<<endl;
            continue;
        }
        if(z[1]==3)
        {
            cout<<"1"<<endl;
            continue;
        }
        if((z[1]==2&&z[2]==2))
        {
            cout<<"2"<<endl;
            continue;
        }
        if((z[1]==2&&z[2]==1&&z[3]==1))
        {
            cout<<"3"<<endl;
            continue;
        }
        if(n==3&&z[1]==2)
        {
            cout<<"2"<<endl;
            continue;
        }
    }
    return 0;
}

 

dfs+贪心

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
int T,n,num[20],ans,p[5];//num代表第i种牌有几个，p代表剩下i张的牌有几种

void rest(int x,int u)
{
    int temp=u;
    bool flag=false;
    if (num[14]&&num[15]) flag=true;//是否有王炸
    memset(p,0,sizeof(p));
    for (int i=1; i<=15; i++) p[num[i]]++;
    if (p[4]!=0)   //四牌特判
    {
        temp+=p[4];
        if (p[2]>=p[4]*2) p[2]-=p[4]*2;//对子够用,四带二 
        else   //对子不够，单张上，四帯一 
        {
            p[4]-=p[2]/2;
            p[2]=p[2]%2;
            if (p[1]>=p[4]*2) p[1]-=p[4]*2;
            else p[1]=p[1]%2;
        }
    }
    if (p[3]!=0)   //同炸弹
    {
        temp+=p[3];
        if (p[2]>=p[3]) p[2]-=p[3];
        else
        {
            p[3]-=p[2];
            p[2]=0;
            if (p[1]>=p[3]) p[1]-=p[3];
            else p[1]=0;
        }
    }
    if (p[2]!=0) temp+=p[2];
    if (p[1]>=2&&flag) temp+=p[1]-1;
    else temp+=p[1];//如果单张剩余2张以上，又存在王炸，那么就把两张单张当成王炸出掉。
    ans=min(ans,temp);
    return;
}
void dfs(int x,int u)//剩余x张牌,已经用了u步 
{
    if (u>=ans) return;//剪枝 
    if (x==0)
    {
        ans=min(u,ans);
        return;
    }
    int start=0,end=0;
    //------单顺-------------
    if (x>=5)
    {
        //每个搜顺子开头都有的小剪枝
        for (int i=1; i<=12; i++)   //注意只能搜到A
        {
            if (num[i-1]==0) start=i;//上一张不够牌，所以这张开始做顺头
            if (num[i]!=0) end=i;//这张是够的，所以顺尾后移
            if (end-start+1>=5)   //如果牌够了
            {
                for (int k=5; k<=end-start+1; k++)
                {
                    //要记得start也可以后移，不然一直只能以start开始顺子，直到start改变
                    start+=k-5;//我就是这里写错调了好久。。。
                    for (int j=start; j<=end; j++) num[j]--;
                    dfs(x-(end-start+1),u+1);
                    for (int j=start; j<=end; j++) num[j]++;
                    start-=k-5;
                }
            }
        }
    }
    start=0;
    end=0;
    //------双顺-------------
    if (x>=6)   //全部同单顺
    {
        for (int i=1; i<=12; i++)
        {
            if (num[i-1]<=1) start=i;
            if (num[i]>1) end=i;
            if (end-start+1>=3)
            {
                for (int k=3; k<=end-start+1; k++)
                {
                    start+=k-3;
                    for (int j=start; j<=end; j++) num[j]-=2;
                    dfs(x-(end-start+1)*2,u+1);
                    for (int j=start; j<=end; j++) num[j]+=2;
                    start-=k-3;
                }
            }
        }
    }
    start=0;
    end=0;
    //------san shun-------------
    if (x>=6)
    {
        for (int i=1; i<=12; i++)
        {
            if (num[i-1]<=2) start=i;
            if (num[i]>2) end=i;
            if (end-start+1>=2)
            {
                for (int k=2; k<=end-start+1; k++)
                {
                    start+=k-2;
                    for (int j=start; j<=end; j++) num[j]-=3;
                    dfs(x-(end-start+1)*3,u+1);
                    for (int j=start; j<=end; j++) num[j]+=3;
                    start-=k-2;
                }
            }
        }
    }
    rest(x,u);//贪心
    return;
}
int main()
{
    scanf("%d%d",&T,&n);
    for (int qwe=1; qwe<=T; qwe++)
    {
        memset(num,0,sizeof(num));
        ans=0x3f3f3f3f;//重要的初始化
        for (int i=1; i<=n; i++)
        {
            int a,b;
            scanf("%d%d",&a,&b);//花色没用，仅仅在大小王上有用
            if (a==0)
            {
                if (b==1) num[14]++;    //大小王视为单张。。。
                if (b==2) num[15]++;
            }
            else
            {
                if (a==1) num[12]++;
                else if (a==2) num[13]++;
                else num[a-2]++;//3->1 4->2 ..... K->11 A->12 2->13 这里是方便搜顺子
            }
        }
        dfs(n,0);
        printf("%d\n",ans);
    }
    return 0;
}

 

//我真的好笨...... 就不想写dfs，就是不对! 唉......
#include<iostream>
#include<cstdio>
#include<cstring>

#define maxn 50

using namespace std;
int poker_cnt[maxn],poker_now[maxn];
int x,y,t,n,ans,cnt,num,pos,start,flag,flag_2,c;

inline int init()
{
    int x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

void work1()
{
    for(int i=1;i<=14;i++)
    {
        if(poker_cnt[i+1]&&poker_cnt[i])
        {
            cnt=0;start=i;pos=i;
            while(poker_cnt[pos]&&pos<=12){cnt++;pos++;}
            if(cnt>=5)
            {
                for(int j=start;j<=start+cnt-1;j++)poker_cnt[j]--;
                n-=cnt;ans++;
            }
        }
    }
}

void work2()
{
    flag=0;
    for(int i=1;i<=14;i++)
    {
        flag_2=0;int pd1=0,pd2=0,pos2=0;
        if(poker_cnt[i]==4)
        {
          for(int j=1;j<=14;j++) for(int k=1;k<=14;k++)
          {
               if(poker_cnt[j]>=1&&poker_cnt[k]>=1&&k!=j&&!flag_2)
               {
                   flag=1;
                   if(poker_cnt[j]==2) pd1=k;if(poker_cnt[k]==2) pd1=j; 
                   for(int l=1;l<=14;l++) 
                  if(poker_cnt[l]==1&&l!=pd1) pd2=1,pos2=l; 
                  if(!pd2)poker_cnt[k]--,poker_cnt[j]--,poker_cnt[i]-=4;
                  else poker_cnt[pd1]--,poker_cnt[pos2]--,poker_cnt[i]-=4;
                  n-=6;ans++;flag_2=1;
               }
               if(poker_cnt[j]==2&&poker_cnt[k]==2&&k!=j&&!flag_2)
               {
                     flag=1;
                  poker_cnt[k]-=2;poker_cnt[j]-=2;poker_cnt[i]-=4;
                  n-=8;ans++;flag_2=1;
               }
          }
          if(!flag) poker_cnt[i]-=4,n-=4,ans++;
        }  
    }
}

void work3()
{
    for(int i=1;i<=14;i++)
    {
        if(poker_cnt[i]==3&&poker_cnt[i+1]==3)
        {
            start=i;pos=i;cnt=0;
            while(poker_cnt[pos]==3){cnt++;pos++;}
            if(cnt>=3)
            {
                n-=cnt*3;ans++;
                for(int i=start;i<=cnt+start-1;i++) poker_cnt[i]-=3;
            }
        }
        if(poker_cnt[i]==2&&poker_cnt[i+1]==2)
        {
            start=i;pos=i;cnt=0;
            while(poker_cnt[pos]==2){cnt++;pos++;}
            if(cnt>=3)
            {
                n-=cnt*2;ans++;
                for(int i=start;i<=cnt+start-1;i++) poker_cnt[i]-=2;
            }
        }
    }
}

void work4()
{
    flag=0;
    for(int i=1;i<=14;i++)
    {
        flag_2=0;
        if(poker_cnt[i]==3)
        {
            for(int j=1;j<=14;j++)
            {
                if(poker_cnt[j]==1&&!flag_2)
                {
                    flag=1;
                    poker_cnt[j]--;poker_cnt[i]-=3;
                    n-=4;ans++;flag_2=1;
                }
            }
            if(!flag) poker_cnt[i]-=3,n-=3,ans++;
        }
    }
}

inline void work5()
{
    for(int i=1;i<=14;i++)
    {
       if(poker_cnt[i])
       {
            n-=poker_cnt[i];ans++;
          poker_cnt[i]=0;
       }
    }
}

int main()
{
    freopen("landlords8.in","r",stdin);
//    freopen("landlords.out","w",stdout);
    t=init();n=init();c=n;int d=n;
    while(t--)
    {
        c=d;n=d;
        flag=0;ans=0;memset(poker_cnt,0,sizeof poker_cnt);
        pos=0;start=0;memset(poker_now,0,sizeof poker_now);
        while(c--){x=init();y=init();poker_cnt[x]++;}
        poker_cnt[14]=poker_cnt[1];poker_cnt[15]=poker_cnt[2];poker_cnt[16]=poker_cnt[0];
        for(int i=3;i<=16;i++) poker_cnt[i-2]=poker_cnt[i];poker_cnt[0]=0;
        poker_cnt[15]=0;poker_cnt[16]=0; 
        if(n>=5) work1();//顺子
        if(n>=4) work2();//四张牌与四带二 
        if(n>=6) work3();//连对，三连对 
        if(n>=4) work4();//三带一  
        if(n) work5();//单 对牌 
        if(n==0) printf("%d\n",ans);
    }
}