树与二叉树知识梳理
树与二叉树知识梳理
树
树的定义
元素有一个前驱和多个后缀
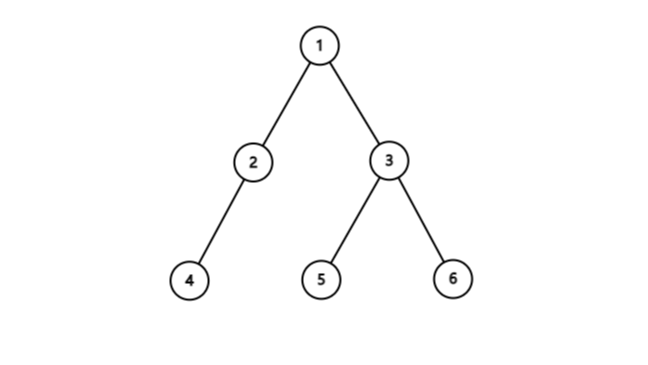
树的常用名词
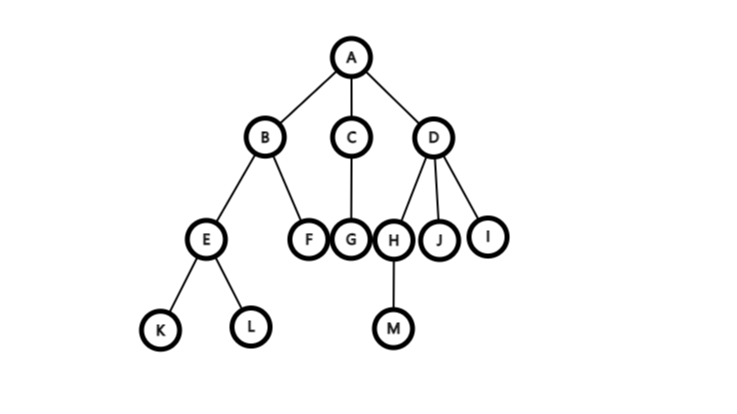
1.节点的度与树的度：一个结点的孩子数目等于这个结点的度，树中各节点的度的最大值称为树的度。
例如：图中E的度是2，树的度是3
2.分支结点与叶子结点：度不为0且不是根结点的结点叫分支结点。度为零的结点叫叶子结点。在分支结点中，每个节点的分支数就是该结点的度。
例如：图中C为分支结点，其度为1，G为叶子结点
3.孩子结点（子女结点）、双亲结点（父结点）、兄弟结点：在一棵树中，每一个结点的后继被称作该结点的孩子结点（子女结点）。相应的，该结点被称作孩子结点的双亲节点（父结点），具有同一个双亲的孩子结点互为兄弟结点。
例如：图中F是B的孩子结点，D是H的父结点，B和D互为兄弟结点
4.节点的层次和树的高度（深度）：树中的每个结点都处在一定的层次上，界点的层次从树根开始定义，根结点为第0层，他的孩子结点为第1层，以此类推。一个结点所在的层次为其双亲结点所在层次加一。树中结点的最大层次成为树的高度（深度）。
例如：图中H为第2层次，树的高度为3
注：在有些资料中，深度是从1开始计算的，也就是说图中H为第3层次，树的高度为4
5.子树：树的一个分支。
例如：图中DHIJM就组成了一个以D为根的子树
6.森林：n（n>=0）个互不相交的树的集合称为森林。
例如：图中子树BEFKL、子树CG、子树DHIJM构成森林
有序树和无序树
有序树和无序树：若树中各节点的子树是按照一定的次序从左向右安排的，且相对次序是不能随意变换的，则称为有序树，否则称之为无序树。
例如：3个相同的结点，组成有序树5种形态
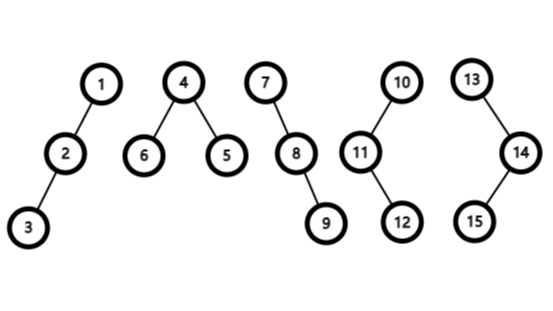
而无序树就只有2种形态
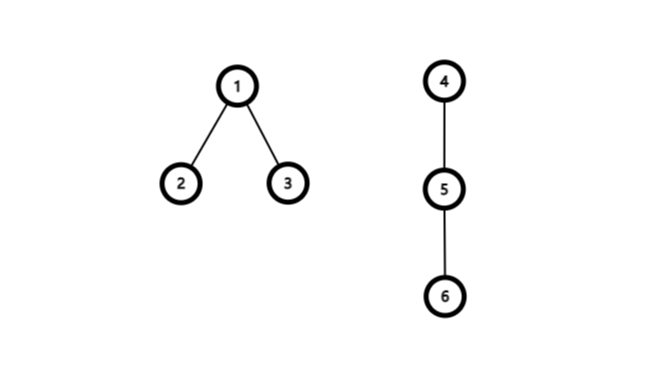
注：有序树和无序树中相同的树，在有序树中它只能为二叉树，在无序树中每个结点可以有多个孩子结点
树的存储
树有两种常见的存储方法——父亲表达发，孩子兄弟表达法
父亲表达法
思路
由于每个结点有多个孩子或兄弟结点，但只要一个父亲结点，所以只要记住自己的父亲是谁就可以建出整棵树了就像母系社会一样
将根结点的父亲设为本身
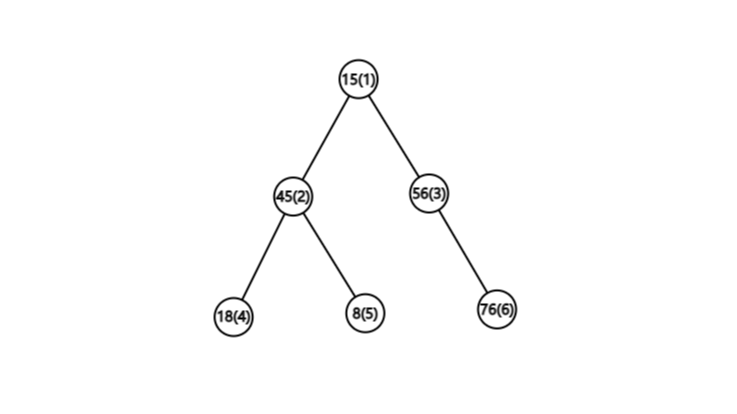
注：括号里的为编号
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 父亲结点下标 | 1 | 1 | 1 | 2 | 2 | 3 |
| 数值 | 15 | 45 | 56 | 18 | 8 | 76 |
代码
void bulid(int i,int x,int y) {//x为y的父亲,i表示第i个结点
parent[i] = x;
data[i] = y;
}
孩子兄弟表达法
思路
虽然每个结点有多个孩子或兄弟结点，但把二者都记录下来同时满足的就只有一种情况，所以这样记录也是可以建出整棵树
注意：储存左边第一个兄弟结点和左孩子，如果没有则为-1
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 孩子结点下标 | 2 | 4 | 6 | -1 | -1 | -1 |
| 兄弟结点下标 | -1 | 3 | -1 | 5 | -1 | -1 |
代码
void build(int i,int x,int y) {//第i个数的孩子为x,父亲为y
child[i] = x;
nex[i] = y;
}
树的遍历
树的遍历指的是访问每一个结点，它分为先根遍历，后根遍历和层次遍历
先根遍历
先根遍历是先访问根结点再访问子树
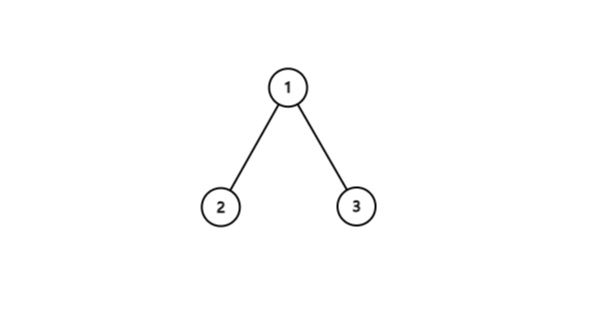
图中数字为遍历顺序
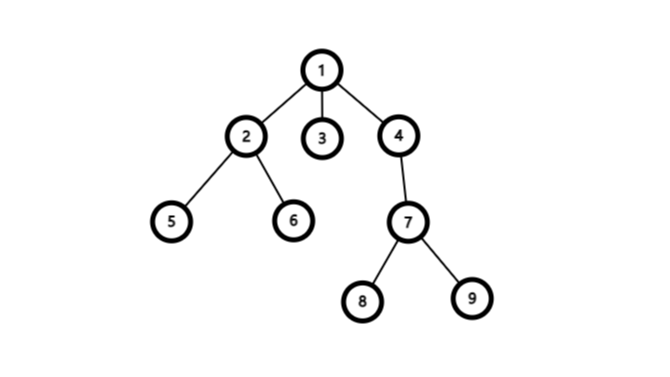
上图中先根遍历的顺序为1->2->5->6->3->4->7->8->9
后根遍历
后根遍历指的是先访问子树再访问根节点
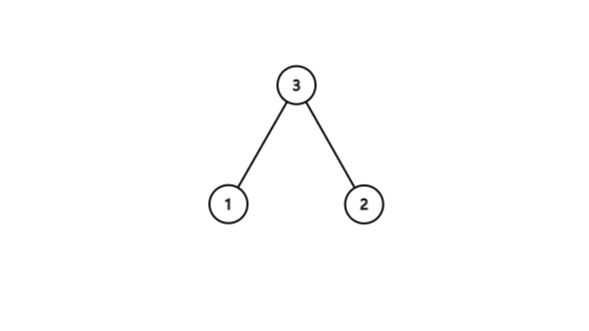
图中数字为遍历顺序
上图中后根遍历的顺序为5->6->2->3->8->9->7->4->1
层次遍历
层次遍历指的是先访问子树再访问根节点
图中数字为遍历顺序
上图中后根遍历的顺序为5->6->2->3->8->9->7->4->1
二叉树
二叉树的定义
1.空树是一棵二叉树
2.二叉树由一个根结点和两棵互不相交的子树构成
3.所有二叉树都是有序树
4.每个结点最多有2个子树，因此其树的度小于等于2
二叉树的性质
1.在二叉树的第i层，最多具有2的i次方个结点（i从0开始）
2.一棵深度为k的二叉树中最多具有2的k+1次方减1个结点
3.对于任意一棵二叉树，如果其叶子结点数为n0,度为2的结点数为n2,则n0=n2+1
4.n个结点的二叉树，深度至少是[log2 n]
满二叉树
满二叉树的定义
满二叉树是二叉树中每层的结点数都达到最大
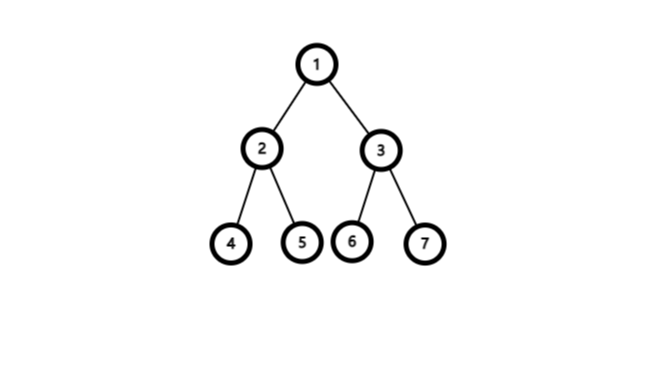
完全二叉树
完全二叉树的定义
完全二叉树是二叉树中除最后一层外其余个层都是满的，最后一层或者是满的。或者是右边缺少连续若干个结点
所以满二叉树是一种特殊的完全二叉树就像长方形和正方形的关系
完全二叉树
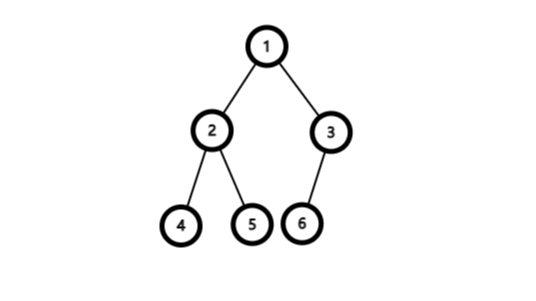
非完全二叉树
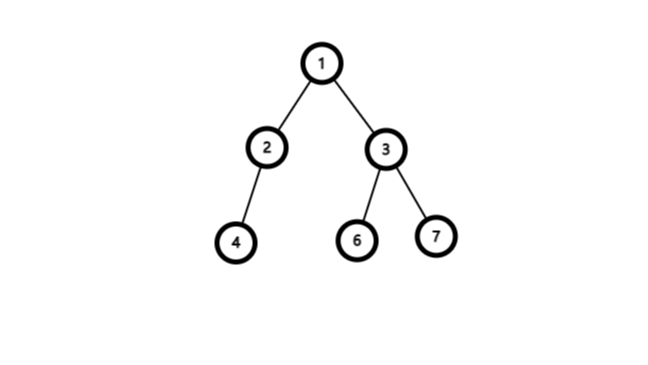
二叉树的存储
二叉树的存储分为4种，父亲表示法，孩子表示法，孩子父亲表示法和完全化
父亲表示法
父亲表示法与基础的树的方法相同
孩子表示法
思路
因为二叉树中每个结点最多有两个孩子，所以我们可以直接记录下它的孩子
如果没有则记为-1
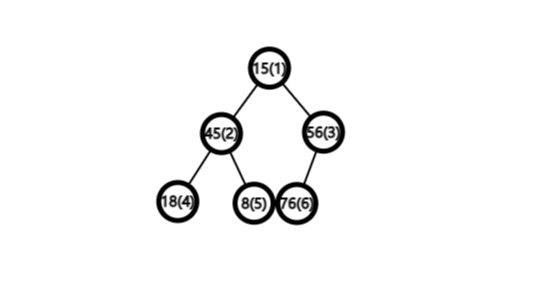
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 左孩子下标 | 2 | 4 | 6 | -1 | -1 | -1 |
| 右孩子下标 | 3 | 5 | -1 | -1 | -1 | -1 |
| 当前数值 | 15 | 45 | 56 | 18 | 8 | 76 |
代码
void build (int i,int x,int y,int z) {//第i个数的数值为x，它的左孩子下标为y，它的右孩子下标为z
data[i] = x;
left_child[i] = y;
right_child[i] = z;
}
孩子父亲表示法
孩子父亲表示法,看字面意思就是记录孩子和父亲的，也就是结合上面两种方法，这种方法会给操作带来一定便捷，但注意这不是所有情况都适用
完全化
完全化是一种很特殊的储存方法，适用于完全二叉树，使用一维数组就可以存储完成
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 数值 | 1 | 2 | 3 | 4 | 5 | 6 |
我们来观察图中的完全二叉树和表格，会发现假设一个数的下标为n，那么它的左儿子的下表为2n，右儿子的下标为2n+1
那么凭借这个规律我们就可以存下整棵完全二叉树
那么我们又有了一个问题，如果它不是一棵完全二叉树呢？
当然，某位大佬早已为我们想好
随然不是，但我们可以把它缺的给补上构造，把空的几位-1
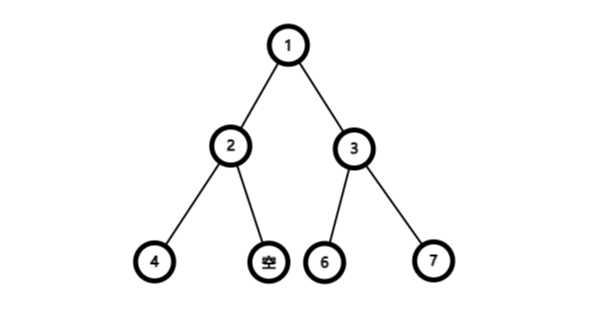
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 数值 | 1 | 2 | 3 | 4 | -1 | 6 | 7 |
代码
void bulid(int i,int x) {//第i个结点的数值为x,传入x判断如果为空，那么传入-1
data[i] = x;
}
二叉树的遍历
二叉树的遍历分为3种先序遍历，中序遍历和后序遍历
先序遍历
思路
先序遍历是先遍历根节点，再遍历左子树，最后遍历右子树
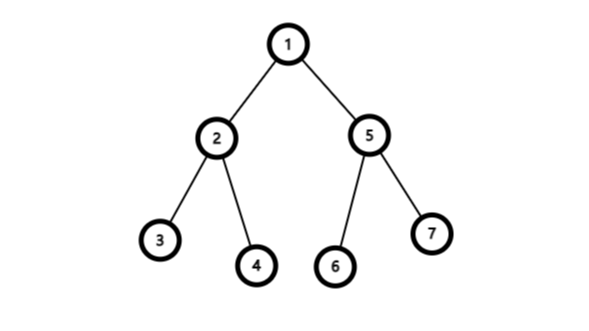
图中数字为遍历顺序
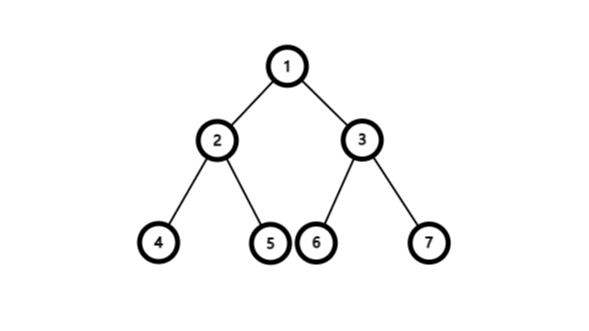
上图中先序遍历的顺序为1->2->3->5->3->6->7
代码
void pre_order(int u) { //u为根节点下标
if(u != -1) {
visit(u);
pre_order(left_child[u]);
pre_order(rihgt_child[u]);
}
return ;
}
中序遍历
思路
中序遍历是先遍历左子树，再遍历根节点，最后遍历右子树
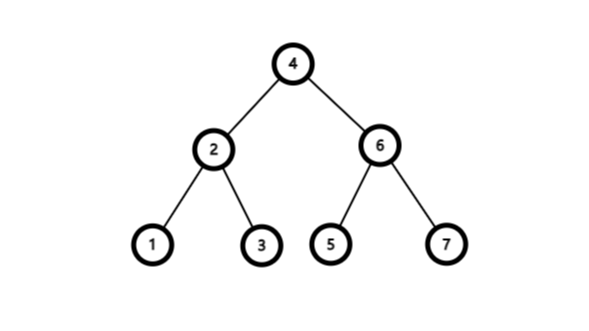
图中数字为遍历顺序
上图中中序遍历的顺序为4->2->5->1->6->3->7
代码
void mid_order(int u) { //u为根节点下标
if(u != -1) {
pre_order(left_child[u]);
visit(u);
pre_order(rihgt_child[u]);
}
return ;
}
后序遍历
思路
后序遍历是先遍历左子树，再遍历右子树，最后遍历根节点
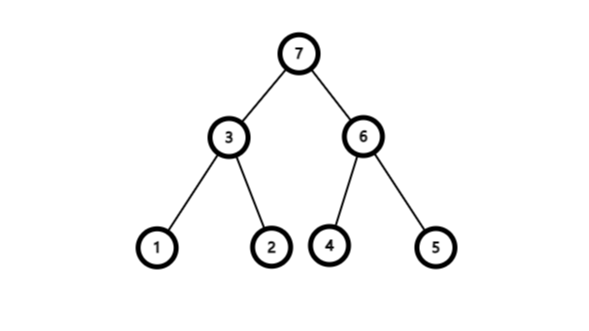
图中数字为遍历顺序
上图中后序遍历的顺序为4->5->2->6->7->3->1
代码
void post_order(int u) { //u为根节点下标
if(u != -1) {
pre_order(left_child[u]);
pre_order(rihgt_child[u]);
visit(u);
}
return ;
}
读者注意：树是一个很重要的数据结构，没读懂可以再读一遍，后面很多知识点要用到
完结撒花
欢迎大家留言
小编蒟蒻一个，有什么问题请大佬不惜赐教Orz
