![在这里插入图片描述]()
这一篇要探讨的是“杨辉三角形的实现以及如何人工走循环”。涉及的知识点和内容很少,主要是想说明如何看懂循环,如何跟着循环走。属于C语言基础篇。
学习编程的人,在学习的初期,几乎都会接触杨辉三角形。但与其说用代码实现输出杨辉三角形是一道编程题,倒不如说它是一道IQ题。因为在杨辉三角形的代码实现过程中,所涉及语法知识和编程概念其实很少。
类似于杨辉三角形这类的编程题还有很多,它们在真正的实际开发中,用的很少,几乎可以说是除了在初学编程阶段以及在面试过程中会接触到之外,你就再也不会遇到了。
这类问题真正难的地方在于它逻辑上面的复杂,很多时候,即便拿到了实现代码,看的也云里雾里的。特别是那些涉及双重循环、三重循环、递归调用、二叉树、双向循环内核链表等等等等的,更烦的是这些东西之间还互相交叉重叠,绕来绕去的简直不要太恶心了。
虽然大多数情况下,我们都不用真正独立写出这些逻辑算法,只要套用前人已有算法的就行了。但是看的懂还是必要的。
所以这篇就简单的分析一下杨辉三角形实现过程中代码运行的流程。跟着流程从头到尾的走一遍程序。虽然对于一些大工程来说,跟着流程走这个过程往往是交由机器来帮我们完成的,像是GDB之类的调试工具。
但是提高自身的阅读代码能力还是很有必要的,否则你跟着GDB一步一步走,程序走错了,你也看不出来,那就毫无意义了。GDB只能说是作为辅助工具,能否调试好代码,还是得看你的代码阅读能力。
好了,先来看一下杨辉三角的实现代码,这篇代码引用自百度百科词条“杨辉三角”(https://baike.baidu.com/item/杨辉三角/215098?fr=aladdin),这里我就不用自己的代码了,以后有机会我想办法会把它再优化一下更新上来的。
#include <stdio.h>
int main()
{
int s = 1, h; // 数值和高度
int i, j; // 循环的计数变量
scanf("%d", &h); // 用户输入层数
printf("1\n"); // 输出第一行 1
for (i = 2; i <= h; s = 1, i++) // 行数 i 从 2 到层高
{
printf("1 "); // 输出该行的第一个 1
for (j = 1; j <= i - 2; j++)//列位置 j 绕过第一个直接开始循环
printf("%d ", (s = (i - j) * s / j));
printf("1\n"); // 输出最后一个 1,换行
}
getchar(); // 暂停等待
return 0;
}
运行结果:
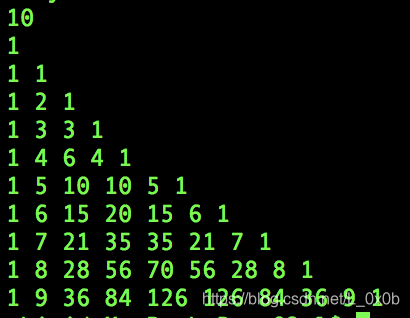
下面我们开始一步一步的跟着程序走下去(建议在电脑上面看的时候把代码复制到编辑器上面,编辑器和浏览器左右分屏对照着看,虽然我每一步都会配图片)。
第一步:程序先是创建了两个变量,一个“s”一个“h”,其中“s”用来临时储存算法运算出来的结果(也就是当前应该输出的值),“h”则是杨辉三角形的高度(也就是需要输出的行数)。

第二步:接收用户的输入,由用户决定杨辉三角形的高度

第三步:输出一个“1”同时换行,也就是手动把第一行给输出完成了。

第四步:然后就是进入了代码的关键算法了(为了方便说明,下面我以用户输入数字“6”为例进行分析,用“-”代替空格方便显示)。
当用户输入“6”的时候,最外层循环的判断条件为“i =2; i<= 6”循环会执行5次。

最外层循环有一个不太常见的用法需要说明一下,在外层循环的末尾循环体中,同时有两个表达式,多出来的“s = 1”的作用是在于控制“s”在每次外层循环开始之前初始化为1。
其实程序中的这一段也可以改为下面这个样子:
外层第一次循环
输出第二行的时候(此时“i = 2, s = 1”):
首先输出“1-”(此时缓冲区里面有“1-”)。
内层循环(“j = 1, j <= 0”)不进入循环(此时缓冲区里面有”1-”)。
结尾输出“1\n”,把缓冲区里面的数据输出到用户的控制面板(此时缓冲区里面有“1-1”)。
外层第二次循环
输出第三行的时候(此时“i = 3, s = 1”):
首先输出“1-”(此时缓冲区里面有“1-”)。
内层循环(“j = 1, j <= 1”)进入一次循环(此时缓冲区里面有”1-”)。
内层第一次循环(“i = 3, j = 1, s = 1”):
s = (3 - 1)*1/1 = 2 输出“2-”(此时缓冲区里面有“1-2-”)。
退出内层循环。
结尾输出“1\n”,把缓冲区里面的数据输出到用户的控制面板(此时缓冲区里面有“1-2-1”)。
外层第三次循环
输出第四行的时候(此时“i = 4, s = 1”):
首先输出“1-”(此时缓冲区里面有“1-”)。
内层循环(“j = 1, j <= 2”)执行两次循环(此时缓冲区里面有”1-”)。
内层第一次循环(“i = 4, j = 1, s = 1”):
s = (4 - 1)*1/1 = 3 输出“3-”(此时缓冲区里面有“1-3-”)。
内层第二次循环(“i = 4, j = 2, s = 3”):
s = (4 - 2)*3/2 = 3 输出“3-”(此时缓冲区里面有“1-3-3-”)。
退出内层循环。
结尾输出“1\n”,把缓冲区里面的数据输出到用户的控制面板(此时缓冲区里面有“1-3-3-1”)。
外层第四次循环
输出第五行的时候(此时“i = 5, s = 1”):
首先输出“1-”(此时缓冲区里面有“1-”)。
内层循环(“j = 1, j <= 3”)执行三次循环(此时缓冲区里面有”1-”)。
内层第一次循环(“i = 5, j = 1, s = 1”):
s = (5 - 1)*1/1 = 4 输出“4-”(此时缓冲区里面有“1-4-”)。
内层第二次循环(“i = 5, j = 2, s = 4”):
s = (5 - 2)*4/2 = 6 输出“6-”(此时缓冲区里面有“1-4-6-”)。
内层第三次循环(“i = 5, j = 3, s = 6”):
s = (5 - 3)*6/3 = 4 输出“4-”(此时缓冲区里面有“1-4-6-4-”)。
退出内层循环。
结尾输出“1\n”,把缓冲区里面的数据输出到用户的控制面板(此时缓冲区里面有“1-4-6-4-1”)。
外层第五次循环
输出第六行的时候(此时“i = 6, s = 1”):
首先输出“1-”(此时缓冲区里面有“1-”)。
内层循环(“j = 1, j <= 4”)执行四次循环(此时缓冲区里面有”1-”)。
内层第一次循环(“i = 6, j = 1, s = 1”):
s = (6 - 1)*1/1 = 5 输出“5-”(此时缓冲区里面有“1-5-”)。
内层第二次循环(“i = 6, j = 2, s = 4”):
s = (6 - 2)*5/2 = 10 输出“10-”(此时缓冲区里面有“1-5-10-”)。
内层第三次循环(“i = 6, j = 3, s = 6”):
s = (6 - 3)*10/3 = 10 输出“10-”(此时缓冲区里面有“1-5–10-10-”)。
内层第四次循环(“i = 6, j = 4, s = 10”):
s = (6 - 4)*10/4 = 5 输出“5-”(此时缓冲区里面有“1-5-10-10-5-”)
退出内层循环。
结尾输出“1\n”,把缓冲区里面的数据输出到用户的控制面板(此时缓冲区里面有“1-5–10-10-5-1”)。
第五步暂停等待程序退出。
![在这里插入图片描述]()
好了,至此杨辉三角的实现过程就算分析完了。
下面这个例子的功能是画一个由字母按照特定顺序排列组成的三角形,感兴趣的也可以看一下。
先看代码
#include <stdio.h>
int main()
{
int i,j;
char ch, n;
scanf("%c",&ch);//C
n = ch-'A'+1; //n=3 //第一次进入 第二次进入 第三次进入
//最外层循环
//一次循环代表输出一行
for(i=1; i<=n; i++) //(i=1;i<=3) (i=2;i<=3) (i=3;i<=3)
{
//内层第一个循环
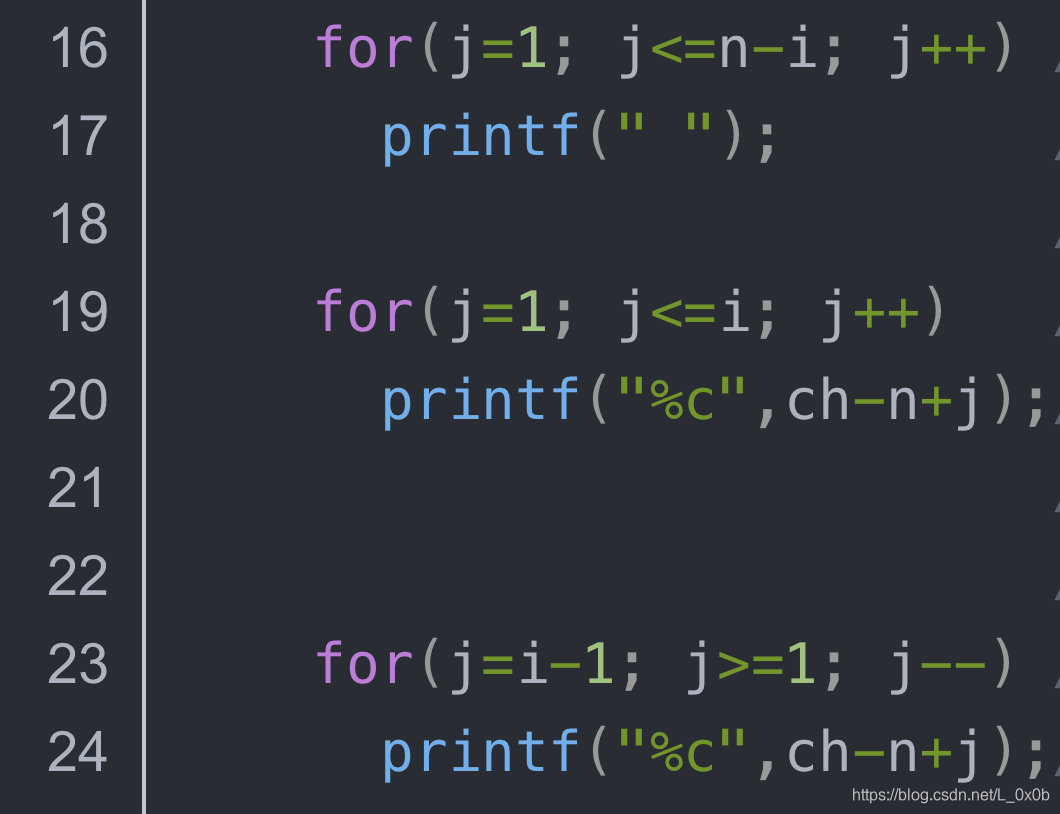
for(j=1; j<=n-i; j++) //(j=1;j<=2) (j=1;j<=1) (j=1;j<=0)
printf(" "); //打了2个空格 打了1个空格 打了0个空格
//内层第二个循环
for(j=1; j<=i; j++) //(j=1;j<=1) (j=1;j<=2) (j=1;j<=3)
printf("%c",ch-n+j);//C-3+1=A C-3+1=A,C-3+2=B C-3+2=B,C-3+3=C
//打了个A 打了A和B 打了B和C
//内层第三个循环
for(j=i-1; j>=1; j--) //(j=0;j>=1) (j=1;j>=1) (j=2;j>=1)
printf("%c",ch-n+j);//不进入循环 C-3+1=A C-3+2=B,C-3+1=A
//什么也没打 打了个A 打了个B和A
printf("\n"); //||A |ABA ABCBA
}
return 0; // ||A
// |ABA
// ABCBA
}
运行结果。

其实过程分析在代码中已经写明白了,不过在这里,我还想逐条逐句再分析一遍,我尽量写的通俗易懂一些。在这个例子里面,分析起来应该还没有太大问题。以后有机会我可能还会分享另外一篇类似这种的人工走循环的逻辑分析文章,在那篇文章中的例子涉及到一个很复杂(至少在我当时是这么觉得的)的三层循环,那个分析起来可能就很费劲了。说实话那篇文章的话,我也不太有信心能把里面的逻辑关系说的很清楚明白。有些东西,你知道是那么一回事,但是却不一定能说的明白,你觉得你自己说明白了,别人却又不一定能听的懂。
在这个例子里面用的是printf()输出,由于printf()有缓冲区的存在,所以输出的数据不会立即出现在用户面板上,只有当遇到要输出“/n”的时候,缓冲区里面的内容才会被推出来。虽然在这个程序里面看不出区别,不过还是要意识到这个缓冲区的存在。
如果不想要
缓冲区的存在这里可以用putchar()来代替printf()作为输出函数,理论上你应该是可以看到用putchar()输出比用printf()输出顺畅不少的,但实际上由于在这个程序里面的输出之间的间隔时间太短,你的肉眼是察觉不到区别的。但是速度快的同时也不是没有牺牲的,这样子做会造成程序对于CPU的占用率提高,降低整体的效率,综合考虑下还是用printf()会比较好。
在开始之前,先说一下这篇代码的整体思路架构。
最外层的for循环用于控制输出的行数。n等于要输出的行数。
内层第一个for循环用于控制输出该行“第一个字母前面的空格”个数。
内层第二个for循环用于控制输出该行“第一个字母到该行中间的最大字母”。
内层第三个for循环用于控制输出该行“中间的最大字母到该行的最后一个字母。
下面我们开始一步一步的跟着程序走下去(建议在电脑上面看的时候把代码复制到编辑器上面,编辑器和浏览器左右分屏对照着看,虽然我每一步都会配图片)。
首先,程序运行到scanf()函数的时候,要求输入(这里其实应该检测一下输入是否合法的,为了方便讲解,就不弄那么麻烦了),这里我们以输入“C”为例进行分析。

当我们输入“C”的时候程序中的n就等于3了。n的作用就在于确定该三角形的层数(既输出的行数),同时也用于计算应该输出的字母。这个代码中用的是分而治之的方法。整体从上到下一行一行的输出。先是控制输出每一行前面的空格,再控制输出从第一个字母开始到该行中间的最大那个字母,然后输出剩下的字母。

题外话:在这里突然想起了一个挺有意思的阅读技巧。有时候看别人的分析解释说明的时候,如果不怎么看的懂,可以试着在脑海中把某些字眼改为自己易于理解的东西。比如把上面那段话中的”输出“两个字改成”画“字,再试着看一遍。
当n = 3的时候,最外层循环一共循环3遍,也就是输出三行。

为了便于说明用“|”代替空格。
输出第一行的时候(i = 1):
内层第
一个for循环的时候(此时缓冲区里面什么都没有:“”):
初始化是“j = 1”判断条件是“j <= 2”所以会循环2次,每一遍输出1个空格,输出2个空格。
内存第二个for循环的时候(此时缓冲区里面有两个空格:“||”):
初始化是“j = 1”判断条件是“j <= 1”所以会循环1次,输出一个A。
内存第三个for循环的时候(此时缓冲区里面有两个空格和一个A:“||A”):
初始化是“j = 0”判断条件是“j >= 1”所以不会进入循环,什么也不输出。
把缓冲区里面的内容输出(此时缓冲区里面有两个空格和一个A:“||A”)。
输出第二行的时候(i = 2):
内层第
一个for循环的时候(此时缓冲区里面什么都没有:“”):
初始化是“j = 1”判断条件是“j <= 1”所以会循环1次,每一遍输出1个空格,输出1个空格。
内层第二个for循环的时候(此时缓冲区里面有一个空格:“|”):
初始化是“j = 1”判断条件是“j <= 2”所以会循环2次,输出一个A和一个B。
内层第三个for循环的时候(此时缓冲区里面有一个空格一个A一个B:“|AB”):
初始化是“j = 1”判断条件是“j >= 1”所以会循环1次,输出一个A。
把缓冲区里面的内容输出(此时缓冲区里面有一个空格一个A一个B一个A:“|ABA”)。
输出第三行的时候(i = 3):
内层第
一个for循环的时候(此时缓冲区里面什么都没有:“”):
初始化是“j = 1”判断条件是“j <= 0”所以不会进入循环,什么也不输出。
内层第二个for循环的时候(此时缓冲区里面什么都没有:“”):
初始化是“j = 1”判断条件是“j <= 3”所以会循环3次,输出一个A和一个B一个C。
内层第三个for循环的时候(此时缓冲区里面有一个空格一个A一个B一个C:“ABC”):
初始化是“j = 2”判断条件是“j >= 1”所以会循环2次, 输出一个B一个A。
把缓冲区里面的内容输出(此时缓冲区里面有一个空格一个A一个B一个C一个B一个A:“ABCBA”)。
最后退出循环结束程序。
好了,说到这里整个程序就算分析完了。初学者阅读一些比较复杂的代码的时候,可以先尝试像代码中那样用注释跟着程序走上一遍。接触多了之后,慢慢的就可以做到把这些步骤都在脑海中走完而不需要写出来了。
附上这个例子的精简版代码:
#include <stdio.h>
int main()
{
int i,j;
char ch;
scanf("%c",&ch);
for(i=0; i<ch-'A'+1; i++)
{
for(j=0; j<=ch-'A'-i; j++)
putchar(' ');
for(j=0; j<=i; j++)
putchar('A'+j);
for(j=i-1; j>=0; j--)
putchar('A'+j);
putchar('\n');
}
return 0;
}
以及数字版的三角形实现代码(这个代码目前只能实现10层以下的三角形,以后有机会再优化):
#include <stdio.h>
int main()
{
int i,j,n;
scanf("%d",&n);
for(i=0; i<n; i++)
{
for(j=0; j<=n-i-1; j++)
putchar(' ');
for(j=0; j<=i; j++)
putchar(j+'1');
for(j=i-1; j>=0; j--)
putchar(j+'1');
putchar('\n');
}
return 0;
}
还有星号符版三角形实现代码(单位为“*”):
#include <stdio.h>
int main()
{
int i,j,n;
scanf("%d",&n);
for(i=0; i<n; i++)
{
for(j=0; j<=n-i-1; j++)
putchar(' ');
for(j=0; j< 2*i+1; j++)
putchar('*');
putchar('\n');
}
return 0;
}
题外话(纯属瞎扯,感兴趣的可以看下)
其实阅读程序不是什么太难的事情,难的还是自己想出来这么一个算法,这个我还真没法说明白是怎么想的出来这些算法的。很多人可以看的懂别人写的算法,知道别人算法的巧妙性,但是要是自己去写的话,却怎么也写不出来,没这个思路,不知道该怎么去写。
感觉嘛,写算法这件事情还是挺需要一点灵性和一点运气的,先是要有个大概的思路,但有时候同一个需求你会想到有很多种不同的实现思路,而且每一个思路都是那种感觉可能行,又有可能不行的样子。在你没有着手去实现这思路之前,你都不知道它的真正可行性。
这就好像你面前同时有好几条路可以走,但是在你没有跟着走下去之前,你又不知道到底那条路是可以走到终点的,有可能是A思路,有可能是B思路,也有可能是AB思路都可以, 更有可能是ABC思路都不可以,走到最后你还是要回到原点去寻找D思路。又或者,可能ABC思路都是可以的,只是你走到了半路以为自己走错路了,走不下去了,没耐心了,看不到希望了,你半路回头去寻找渺茫的D思路去了而已。这些都有可能。
或者,你运气还算好,一开始就选对了路,一路坚持走到了终点。但是,你有没有想过,除了你选的A思路是可行的以外,C思路也是可行的。而且如果你一开始顺着C思路走,整个代码实现的流程将会更加简洁,逻辑结构将会更加清晰,同时程序运行的效率也会更加高效呢?而这所有的所有,如果你不先尝试性的走出第一步,你永远都不会知道。
我的方法是,觉得这个思路可行,就尝试性的去实现它,不撞南墙不回头,撞了再回头。很多时候,你一开始只有一个思路,但是在你实现这个思路的过程中,你慢慢的又会突然之间灵光一闪,又想到了另外一个思路。有时候人脑就是这么一个神奇的东西。你不断的去接触一个问题,接触的多了,灵感就这么突然来了。
实现一个算法是一件很有成就感又很惊喜的事情。就好像第二篇代码中的那个变量n,它本身即可以用来控制输出的行数,又可以参与到内层循环中通过运算实现别的功能。这种感觉就好像是自己一开始定义n这个变量仅仅只是为了用来控制输出行数的,但是你写代码的过程中却突然发现这么一个自己随手写的变量,在你想实现别的功能的时候,竟然很巧合的可以用来干一些别的事情。你突然就会很惊喜自己怎么这么聪明啊,竟然写出了这么巧妙的代码(虽然你一开始真没这么想过),然后你就会把你的代码拿给你的同学看,然后自豪的说你在写这篇代码的时候,一开始就想好了这个算法了,巧妙的利用了这个地方的重合,减少了代码重复性的同时又节约了内存,满满的成就感油然而生(此处应该有掌声)。哈哈哈,开个玩笑(虽然我经常就是这么干的)。
但是写算法的过程中确实经常会遇到这种情况的,有时候一个变量同时有好几种用途,这种情况我也不知道该怎么解释,感觉冥冥中总有某些东西连接着整个算法,使得某些算法可以做到很巧妙,很完美,很无可挑剔。
这说的有点玄,就像是你为了一个大需求下面的某个小需求创建了一个变量,那么这个变量就很有可能会和大需求下面的其他小需求产生一些直接或者间接的关系,然后这个变量就很有可能会有多种用途。可能是由于事物不同属性之间总会或多或少有着某种联系的原因吧。
就好像你的需求是计算一个长方体,你在计算它的面积的时候创建了长宽的变量,然后你在计算它的体积的时候突然发现你前面的长宽变量也可以用来二次使用。虽然这种关系在平时编程开发面对具体需求的时候可能表现不是那么明显,虽然我没法证明,但我觉得这种东西是真的存在的。
否则为什么有些代码的算法就是可以做到那么巧妙,那么完美,那么无可挑剔呢?或者也仅仅是巧合,是由于人类的主观能动性,使得我们更倾向于去寻找程序算法中的各种巧合然后加以利用吧!不过我感觉嘛,应该是要先存在着那层巧妙的联系,而后我们才能把这层巧妙的联系寻找出来加以利用的。
其实有时候我真觉得这个世界真是奇妙,明明你在写一个算法的时候没有想过太多,就这么用最笨的办法一路跌跌撞撞的走到了终点,但是当你回过头来看一下你原来走过的路,你又总能找到一些捷径,就好像这些捷径是必然存在一样。说的有点玄对吧?我其实就是在说算法优化啦。
写在后面
一开始我在翻找我以前写的代码寻找素材的时候,找到了一个画三角形的代码,而且乍一看还挺像杨辉三角形的,于是这篇文章我的创作初衷就是为了详细分析一下杨辉三角形的实现流程的。但在分析的过程中越写越觉得不对劲,因为杨辉三角形的概念我大概还是有点印象的。
最后不放心才再去查了一下杨辉三角形的结构,才发现我找到的代码不是画杨辉三角形的,但是我整篇文章都快要定稿了都。然后我看着文章发呆了很久,在想怎么去改。最终的决定方案是——我同时再把杨辉三角形也给分析完算了。
当时22点(原本计划是十二点之前完成这篇文章然后美美的睡一觉的,结果熬到了现在),然后我就先去洗了个澡,洗完衣服再晾起来之后就已经23点多了。从23点半到1点半这段时间,我都是在想办法用自己的算法去实现画杨辉三角形的功能,但是很惭愧的说,一直到2点我都没想到很好的办法。
这期间我也不是没想过用数组来储存然后再输出,网上的代码也大多数是用这个方法的,但用数组的方法就和这篇文章要讨论循环算法内容不太对的上,就放弃了。我甚至想过用链表来创建队列,利用队列或栈的存储特点来实现,还想过用二叉树来实现。但都不是我想要的,我真正想要的实现过程就是像这篇文章中的第一个例子那样,单纯的用循环和算法来实现画杨辉三角形。
只有用这种方式的代码才是最高效的。所以我才引用了文章中那个例子的代码来分析,感谢原作者。大概3点的时候我才开始动手写分析,现在刚好5点完稿,还要上传加排版,希望6点前能睡觉吧!
原博客始发于CSDN,在如今博客界的转载抄袭泛滥的环境下,原创不易,点个赞再走呗。以下是博客首页的链接。







 浙公网安备 33010602011771号
浙公网安备 33010602011771号