做题记录
懒得弄链接了,好烦
口胡的会标注出来(但应该会把代码补上)
都是 lxm 几年前就切掉的题
发现每个题都是在 lxm 的嘲讽下完成的
发现我做的题竟然大部分都是去年集训队作业,可我是找了某知名博主博客看的啊今年的集训队作业都没怎么补啊
之后可能会加进去一些最近考的 2600 以上的 CF 题
追随 lxm 的脚步开始补 AGC
AGC023D
sb 想法是直接往自己家走,被 lxm 无情叉了:

如果往自己家的方向投,那就是 车 \(\rightarrow 2 \rightarrow 6 \rightarrow 5\) ,对 \(5\) 来说不优,所以 \(5\) 应该往相反方向投。
摸一下发现只需要管最左边和最右边的,看到底决定往哪边走,然后把最先到的点到达,剩下的就是子问题了。
code
#include<bits/stdc++.h>
#define it register int
#define ct const int
#define il inline
const int N=1000005;
int n,m,x[N];
long long ans,p[N];
int main(){
scanf("%d%d",&n,&m);it i;
for(i=1;i<=n;++i) scanf("%d%lld",&x[i],&p[i]);
it l=1,r=n,dir=2;
while(l<r&&x[l]<m&&x[r]>m){
if(p[l]<p[r]) p[r]+=p[l],dir!=0?ans+=std::abs(x[r]-x[l]),dir=0:0,++l;
else p[l]+=p[r],dir!=1?ans+=std::abs(x[r]-x[l]),dir=1:0,--r;
}
x[l]>m?ans+=x[r]-m:ans+=m-x[l],printf("%lld",ans);
return 0;
}
AGC030C
随手摸了一下感觉自己很牛逼,然后 lxm 说 \(K \leq 1000\) ,我的构造只能满足 \(K \leq 500\)。(\(K=2n\) 指的是 \(K\) 是偶数)
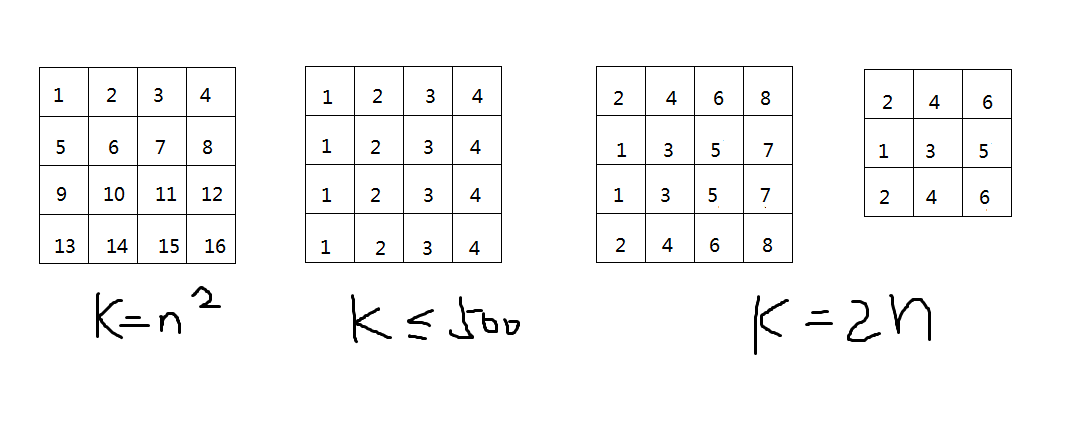
然后又摸了一个多小时终于摸了个像话的东西:
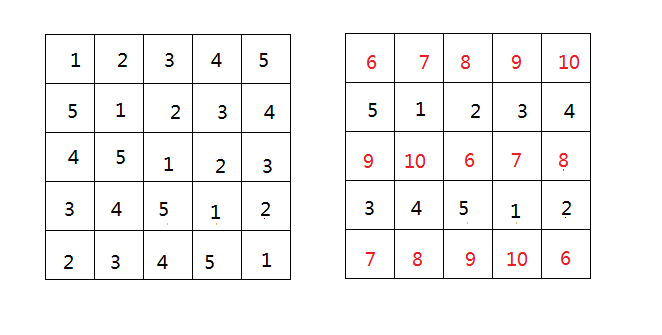
相当于斜着填,每多一种颜色就拿一个颜色出来隔花填 (斜着看!)
code
#include<bits/stdc++.h>
#define it register int
#define ct const int
#define il inline
const int N=505;
int K,n,a[N][N];
int main(){
scanf("%d",&K),n=(K<500?K:500),printf("%d\n",n);
for(it i=1;i<=n;++i){
it t=0;
for(it j=i;j<=n;++j)
a[i][j]=++t;
for(it j=1;j<i;++j)
a[i][j]=++t;
}
K-=n;
for(it i=1;i<=n;++i)
if(i&1){
it t=0;
for(it j=i;j<=n&&t<K;++j)
a[i][j]+=n,++t;
for(it j=1;j<i&&t<K;++j)
a[i][j]+=n,++t;
}
for(it i=1;i<=n;++i,puts(""))
for(it j=1;j<=n;++j) printf("%d ",a[i][j]);
return 0;
}
ARC101E (口胡)
lxm 一分钟就会了,太强了。
考虑每条边都覆盖很麻烦,于是容斥掉不合法的情况。
设 \(F_{i,j}=i\) 为根的子树内, \(i\) 所在的连通块大小为 \(j\) 的方案数。
发现一些没有被覆盖的边把树分成了一堆连通块,而每个连通块的贡献 \(W(k)=(siz_i-1)(siz_i-3)...\times 5 \times 3 \times 1 \ \ (2|siz_i)\) , 就考虑一开始选一个点,剩下 \(n-1\) 个都可以和他配,然后把他俩删掉,剩下的依此类推。
于是可以枚举每个孩子所在的连通块大小。考虑每次如果是扣掉一个孩子,直接 \(g_j -= f_{i,j} \times f_{v,k} \times W(k)\) ;如果是加上,那么它的 \(siz\) 会变大,所以 \(g_{j+k} += f_{i,j} \times f_{v,k}\) 。
最后的答案应该是 \(\sum_{2|i} f_{1,i} \times W(i)\)。
code
#include<bits/stdc++.h>
#define it register int
#define ct const int
#define il inline
using namespace std;
#define P 1000000007
const int N=100005;
int n,u,v,t,w[N],ans,f[5005][5005],g[N],h[N],nxt[N],adj[N],sz[N],fa[N];
il void add(){nxt[++t]=h[u],h[u]=t,adj[t]=v,nxt[++t]=h[v],h[v]=t,adj[t]=u;}
il void dfs(ct x){
f[x][1]=sz[x]=1;
for(it i=h[x],v;i;i=nxt[i])
if((v=adj[i])^fa[x]){
fa[v]=x,dfs(v);
for(it j=1;j<=sz[x];++j)
for(it k=1;k<=sz[v];++k)
g[j+k]=(g[j+k]+(0ll+f[x][j])*f[v][k])%P,g[j]=(g[j]-(0ll+f[x][j])*f[v][k]%P*w[k])%P;
sz[x]+=sz[v];
for(it j=0;j<=sz[x];++j) f[x][j]=g[j],g[j]=0;
}
}
int main(){
scanf("%d",&n);it i;
for(i=1;i<n;++i) scanf("%d%d",&u,&v),add();
for(i=2,w[0]=1;i<=n;++i) w[i]=(0ll+w[i-2])*(i-1ll)%P;
dfs(1);
for(i=2;i<=n;i+=2) ans=(ans+(0ll+w[i])*f[1][i])%P;
printf("%d",ans<0?ans+P:ans);
return 0;
}
CF521D
看懂题意之后就是 sb 题 。 —— by lxm
发现每个数独立;乘法不管怎么选最后对答案的贡献都是固定的,所以一定会选一堆最大的;赋值只会在开头来一次或者不来;加法也是从大到小选,把每个人的加法操作从大到小排个序,发现它只会选一个前缀操作,于是就相当于乘法了。确实不难。
code
#include<bits/stdc++.h>
#define it register int
#define ct const int
#define il inline
using namespace std;
typedef long long ll;
const int N=1000005;
int n,m,K,a[N],op[N];
vector<int> ans;
vector<pair<int,int> > g[N][2];
vector<pair<double,int> > mul;
int main(){
scanf("%d%d%d",&n,&m,&K);it i,j;
for(i=1;i<=n;++i) scanf("%d",&a[i]);
for(i=1;i<=m;++i){
it u,v;
scanf("%d%d%d",&op[i],&u,&v),--op[i];
if((!op[i])&&v<=a[u]) continue;
if(op[i]==2){mul.push_back(make_pair(v,i));continue;}
g[u][op[i]].push_back(make_pair(v,i));
}
for(i=1;i<=n;++i){
if(!g[i][0].empty()) std::sort(g[i][0].begin(),g[i][0].end()),std::reverse(g[i][0].begin(),g[i][0].end()),g[i][1].push_back(make_pair(g[i][0][0].first-a[i],g[i][0][0].second));
std::sort(g[i][1].begin(),g[i][1].end()),std::reverse(g[i][1].begin(),g[i][1].end());
double x=a[i];
for(const auto&p : g[i][1]) mul.push_back(make_pair((x+p.first)/x,p.second)),x+=p.first;
}
vector<int> ans;
std::sort(mul.begin(),mul.end()),std::reverse(mul.begin(),mul.end());
for(it i=0;i<K&&i<mul.size();++i) ans.push_back(mul[i].second);
std::stable_sort(ans.begin(),ans.end(),[&](ct p,ct q){return op[p]<op[q];});
printf("%d\n",ans.size());
for(const int &p : ans) printf("%d ",p);
return 0;
}
ARC093E
这是 ygp 在我们初三的时候给我们考的题 。 —— by lxm
钦定某条边必须选为最小生成树的边,算出现在的 \(MST = w\) ,整个图的 \(MST = mn\) 。
-
\(w<mn\) 这条边只能和他所在的生成树染成一个颜色,染色方案为 \(2\)
-
\(w>mn\) 这条边以及其所在的生成树怎么染答案都没有影响,假设这样的边有 \(t\) 条,染色方案为 \(2^t\)
-
\(w=mn\) 这些边的颜色不能全和前面的一样,假设有 \(k\) 条,染色方案为 \(2^{k}-1\)
然后就做完了。
code
#include<bits/stdc++.h>
using namespace std;
const int md=1e9+7;
const int N=2145;
#define ll long long
struct ask{int x,y,z;}a[N];
int n,m,ct,f[N];
bool cmp(ask a,ask b){return a.z<b.z;}
ll x,mn,as=1,tt=1;
int find(int x){return f[x]?f[x]=find(f[x]):x;}
int main(){
scanf("%d%d%lld",&n,&m,&x),mn=x;
for(int i=1;i<=m;i++)scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
sort(a+1,a+m+1,cmp);
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++)f[j]=0;
ll r=a[i].z;f[a[i].x]=a[i].y;
for(int j=1;j<=m;j++){
int x=find(a[j].x),y=find(a[j].y);
if(x==y)continue;
f[x]=y,r+=a[j].z;
}
mn=min(mn,r);
if(r>x) as=as*2%md;
if(r==x)++ct;
}if(mn==x)ct--;
for(int i=1;i<=ct;i++)tt=tt*2%md;
tt=(tt-1+md)%md;
if(!ct&&mn!=x) puts("0");
else printf("%lld\n",as*tt%md*2%md);
return 0;
}
AGC035E (口胡)
人傻了,根本想不到。(lxm : 这题还行)
考虑这样一个操作:假如我先删了 \(x-2\) ,又删了 \(x\) ,这时候我多出来一个 \(x-2\) ,那我又可以删除 \(x-2\) ,这样的操作是没有必要的,那么我们一定要让操作没有成环的情况。
那么我们把 \(x\) 向 \(x-2\) 和 \(x+K\) 连有向边,如果成环就会挂。
首先我们把 \(K\) 奇偶分类,都不能出现长度为 \(\frac{k}{2}+1\) 连续删的。
考虑什么情况是环: (直接用的hyw小姐姐博客的图,谢谢小姐姐 OwO)
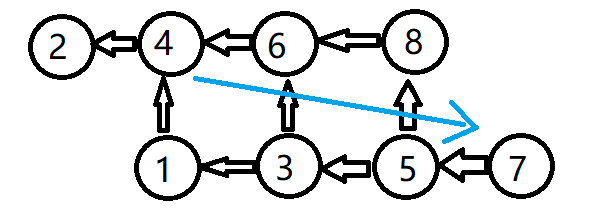
就是向左 \(\rightarrow\) 向上 \(\rightarrow\) 向左
直接 dp ,设 \(f[i][j][k]\) 表示前 \(i\) 层路径上一共 \(j\) 个点,奇数连续选了 \(k\) 个的方案数,转移的时候注意没有环,逐层做即可。
CF605E
发现正着做不太好做,考虑倒着做。
设 \(E_i\) 表示 \(i\) 到 \(n\) 的答案。考虑对于 \(i\) 上一个走的 \(j\):
就是如果 \(E_k < E_j\) ,那么除非 \(k\) 比 \(j\) 后出现,不然会去选 \(k\) 。然后还要除掉走不通的情况。
直接 dp ,枚举没更新的最小值更新就好了。
code
#include<bits/stdc++.h>
#define it register int
#define ct const int
#define il inline
using namespace std;
typedef long long ll;
typedef double db;
const int N=1005;
int n;
bool vs[N];
db p[N][N],prod[N],E[N];
int main(){
scanf("%d",&n);it i,j,k;
if(n==1) return puts("0.0000000000"),0;
for(i=1;i<=n;++i)
for(j=1;j<=n;++j)
scanf("%d",&k),p[i][j]=k*0.01;
vs[n]=1;
for(i=1;i<n;++i) E[i]=1,prod[i]=1-p[i][n];
for(i=1;i<=n;++i){
db mn=1e18;k=0;
for(j=1;j<=n;++j) if((!vs[j])&&E[j]/(1-prod[j])<mn) mn=E[j]/(1-prod[j]),k=j;
if(k==1) return printf("%.12lf",E[1]/(1-prod[1])),0;
for(j=vs[k]=1;j<=n;++j) E[j]+=E[k]/(1-prod[k])*p[j][k]*prod[j],prod[j]*=(1-p[j][k]);
}
return 0;
}
CF521E (口胡)
wd 姐姐教我做题!
发现如果两点之间有三条以上的不相交路径一定有两个以上边相交的环。然后发现如果我们把原图的生成树弄出来,那么两点之间一定有一条路径,于是只要两点之间的树边都被非树边覆盖了两次就一定可以满足。这个可以用树上差分来解决。
AGC027D
啊,摸出来了 \(\mathtt{lcm} + 1\) ,可惜压根没往质数上面想。lxm 直接把我叉爆了。
考虑对图黑白染色,然后依次按质数拉斜线,黑点就是交线两质数的乘积,白点就是周围四个点的 \(\mathtt{lcm}+1\) 。
要注意质数的顺序,不然会超过限制。
(用一下粉兔博客里面的图,谢谢兔队)
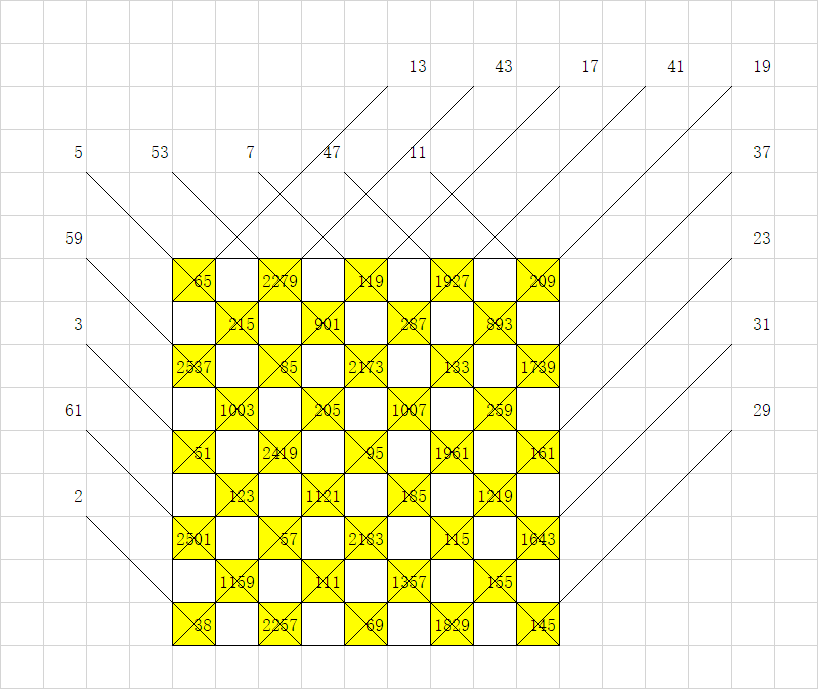
code
#include<bits/stdc++.h>
#define it register int
#define ct const int
#define il inline
using namespace std;
const int N=1000005;
int n,p[N],cnt;
bool isp[N];
long long a[505][505];
il void Pre(ct n){
for(it i=2,j,x;i<=n;++i){
if(!isp[i]) p[++cnt]=i;
for(j=1;(x=i*p[j])<=n;++j){
isp[x]=1;
if(!(i%p[j])) break;
}
}
}
template<class I>
il I lcm(I a,I b){return a&&b?(a/__gcd(a,b)*b):(a|b);}
int main(){
scanf("%d",&n);
if(n==2) return puts("4 7"),puts("23 10"),0;
Pre(n<<4);
for(it i=1;i<=n;++i)
for(it j=((i&1)^1)+1;j<=n;j+=2)
a[i][j]=(0ll+p[i+j>>1])*p[n+(i-j>>1)+(n+1>>1)];
for(it i=1;i<=n;++i)
for(it j=(i&1)+1;j<=n;j+=2)
a[i][j]=lcm(lcm(a[i-1][j],a[i+1][j]),lcm(a[i][j-1],a[i][j+1]))+1;
for(it i=1;i<=n;++i,puts(""))
for(it j=1;j<=n;++j)
printf("%lld ",a[i][j]);
return 0;
}
AGC027F (已做,占坑)
占坑
CF611H
什么神仙题,摸吐了都没摸出来(
最初的思路就是,每次把 \(10^i\) 作为这个位数的 “联络员”,就是不管啥都往它身上连,但是判断环什么的比较麻烦,弄不出来。
去膜了题解,发现可以这样:
一棵树相当于每条边和点之间的完美匹配。
把每个点的位置看成它的颜色,那么最多只有 \(5\) 种颜色。
把颜色相同的放一起考虑,颜色不同的拿出来看能不能连边。
发现这是二分图,考虑 Hall 定理:
- 如果二分图 \((X,Y)\) 存在完美匹配且 \(|X| \leq |Y|\) , 那么对于 \(X\) 的每个子集 \(S\) , 它向另一边连的点数都要 \(\geq |S|\)
由于这题范围小,可以直接暴力枚举子集做。
code
#include<bits/stdc++.h>
#define it register int
#define ct const int
#define il inline
using namespace std;
const int N=15;
int n,m,lim,pw[N],cn[N][N],num[N],u,v;
bool vs[N];
string s1,s2;
il bool ck(){
for(it s=1,i,j;s<lim;++s){
it cna=0,cnb=0;
for(i=1;i<=m;++i) if(s>>(i-1)&1) cna+=num[i];
for(i=1;i<=m;++i) for(j=i;j<=m;++j) if((s>>(i-1)&1)|(s>>(j-1)&1)) cnb+=cn[i][j];
if(cna>cnb) return 0;
}
return 1;
}
int main(){
ios::sync_with_stdio(false);
cin>>n;it i;
for(i=pw[1]=1;pw[i]<=n;++i) pw[i+1]=pw[i]*10;m=i-1,lim=(1<<m)-1;
for(i=1;i<m;++i) num[i]=pw[i+1]-pw[i];num[m]=n-pw[m]+1;
for(i=1;i<n;++i) cin>>s1>>s2,u=s1.length(),v=s2.length(),++cn[u][v],u^v?++cn[v][u]:0;
if(!ck()) return puts("-1"),0; vs[1]=1,++pw[1],--num[1];
for(it s=1;s<n;)
for(i=1;i<=m;++i)
if(vs[i])
for(it j=1;j<=m;++j)
if(cn[i][j]&&num[j])
--cn[i][j],--num[j],i^j?--cn[j][i]:0,ck()?printf("%d %d\n",pw[i]-1,pw[j]),++pw[j],vs[j]=1,++s:(++cn[i][j],++num[j],i^j?++cn[j][i]:0);
return 0;
}
CF578E
考虑一个简单的贪心:每次把在 \(i\) 后面的最靠前的合法位置拿出来放到 \(i\) 后面,如果不存在那就只能往回走到第一个合法位置,代价为 \(1\)。这个可以简单用 \(set\) 维护一下。
但这个贪心会挂,反例:现在我们在一个 \(L\) 上,他后面的合法位置都是 \(R\) , 并且第一个合法位置也是 \(R\), 那我们应该花 \(1\) 的代价走到第一个合法位置。反之则亦然。
code
#include<bits/stdc++.h>
#define it register int
#define ct const int
#define il inline
using namespace std;
const int N=1000005,inf=2e9;
int n,ans;
char s[N];
set<int> S[2];
vector<int> o;
int main(){
scanf("%s",s+1),n=strlen(s+1);it i;
for(i=1;i<=n;++i) S[s[i]=='L'].insert(i);
S[0].insert(inf),S[1].insert(inf);
if(S[1].size()<S[0].size()||(S[1].size()==S[0].size()&&*S[1].begin()>*S[0].begin())) std::swap(S[1],S[0]);
for(it i=1,j=1,x=*S[1].begin();i<=n;++i,j^=1){
if(x==inf||(*S[j^1].lower_bound(x)==inf&&*S[j].begin()!=x&&*S[j].begin()<*S[j^1].begin())) ++ans,x=*S[j].begin();
S[j].erase(x),o.push_back(x),x=*S[j^1].lower_bound(x);
}
printf("%d\n",ans);
for(const int &x : o) printf("%d ",x);puts("");
return 0;
}
CF1539F
不知道算不算自己摸的,毕竟细节还稍微瞄了一下题解。
考虑这个最大距离的定义,假设现在的数为 \(x\) ,记 \(<x\) 的数有 \(l\) 个,\(>x\) 的数有 \(r\) 个,\(=x\) 的数有 \(s\) 个。
现在只需要对这种形式的式子取 \(\max\) ,易发现我们每次要最大化或最小化 \(mid\) ,可以线段树,然后倒着来一遍。
code
#include<bits/stdc++.h>
#define it register int
#define ct const int
#define il inline
using namespace std;
const int N=1000005;
struct ky{
int s,l,r;
}s[N];
il int Max(ct p,ct q){return p>q?p:q;}
il void ckMax(it&p,ct q){p=(p>q?p:q);}
il ky operator + (const ky&a,const ky&b){return (ky){a.s+b.s,Max(a.l,a.s+b.l),Max(b.r,b.s+a.r)};}
int n,a[N],p[N],ans[N];
il void B(ct rt,ct l,ct r){
if(l==r) return s[rt]=(ky){-1,-1,-1},void();
ct mid=l+r>>1,ls=rt<<1,rs=ls|1;
B(ls,l,mid),B(rs,mid+1,r),s[rt]=s[ls]+s[rs];
}
il void upd(ct rt,ct l,ct r,ct pos){
if(l==r) return s[rt]=(ky){1,1,1},void();
ct mid=l+r>>1,ls=rt<<1,rs=ls|1;
pos<=mid?upd(ls,l,mid,pos):upd(rs,mid+1,r,pos),s[rt]=s[ls]+s[rs];
}
il ky que(ct rt,ct l,ct r,ct u,ct v){
if(l>=u&&r<=v) return s[rt];
ct mid=l+r>>1,ls=rt<<1,rs=ls|1;
if(v<=mid) return que(ls,l,mid,u,v);
if(u>mid) return que(rs,mid+1,r,u,v);
return que(ls,l,mid,u,mid)+que(rs,mid+1,r,mid+1,v);
}
int main(){
scanf("%d",&n);it i;
for(i=1;i<=n;++i) scanf("%d",&a[i]),p[i]=i;
std::sort(p+1,p+1+n,[&](ct p,ct q){return a[p]<a[q];});
B(1,1,n);
for(it i=1,j=1;i<=n;i=j){
while(j<=n&&a[p[j]]==a[p[i]])
upd(1,1,n,p[j]),++j;
for(it k=i;k<j;++k)
ckMax(ans[p[k]],(que(1,1,n,1,p[k]).r+que(1,1,n,p[k],n).l>>1)-1);
}
B(1,1,n);
for(it i=n,j=n;i;i=j){
while(j&&a[p[j]]==a[p[i]])
upd(1,1,n,p[j]),--j;
for(it k=i;k>j;--k)
ckMax(ans[p[k]],que(1,1,n,1,p[k]).r+que(1,1,n,p[k],n).l-1>>1);
}
for(i=1;i<=n;++i) printf("%d ",ans[i]);
return 0;
}
CF1526F (口胡,占坑)
挺神仙的。首先观察到 \(p_1<p_2\) 且 询问次数为 \(2n+420\) ,这是一个提示。
CF1535F (口胡)
首先考虑只有两个串 \(S_1,S_2\),怎么求 \(f(S_1,S_2)\) ?
我们发现 \(f(S_1,S_2) \leq 2\):因为可以找任意一个串的子串排序,最多只需要各排序一次。
所以 \(F=0\) 就是两串相等,\(F=1337\) 就是两串的字母种类和个数不一样,\(F=1\) 就是除去两串的 \(lcp\) 和 \(lcs\) 剩下某串是升序的。
那么现在的问题就是怎么快速求。(摸晕了只会数据分治做法,而且还难写,还是看题解去)
考虑把所有字符串排序,那么 \(a_i\) 与 \(a_{i+1},a_{i+2},\cdots,a_n\) 的 \(lcp\) 长度是单调不增的,那么我们根据不同的 \(lcp\) 进行划分,每次二分最长的上升序列位置即可。
统计数量可以利用 \(Trie\) 树,把反串插到 \(Trie\) 树里面,每次在上面跑即可。
CF1523F
摸了半天细节还是有点不清楚。看范围发现可以直接状压。首先对于每个点 \(x\) ,先预处理每个传送门 \(i\) 到它所需要最少的时间 \(t_{i,x}\),然后状压 dp,设 \(f_{i,s}\) 表示已经去过的传送门集合为 \(s\) ,得了 \(i\) 分的最小时间;\(g_{i,s}\) 表示已经去过的传送门集合为 \(s\) ,走到 \(i\) 这个地点可以获得的最大得分。
考虑如何转移:
-
从某点直接走到下一个点
-
从某点走到一个没去过的传送门
-
从某点瞬移到一个去过的传送门
-
从某传送门走到某点
-
从某传送门走到另一没去过的传送门
(只有第三个的贡献不是曼哈顿距离而是 \(1\) )
两个数组互相之间转移即可。有亿点细节。
code
#include<bits/stdc++.h>
#define it register int
#define ct const int
#define il inline
using namespace std;
const int N=1<<14,inf=1061109567;
struct ky{
int x,y,t;
}a[N];
int n,m,x[N],y[N],f[N][120],g[N][120],dis[N][120],ds[120][120];
il int A(ct x){return x<0?-x:x;}
il void ckMin(it &p,ct q){p=(p<q?p:q);}
il void ckMax(it &p,ct q){p=(p>q?p:q);}
int main(){
scanf("%d%d",&n,&m);it i,j,s;
for(i=0;i<n;++i) scanf("%d%d",&a[m+i].x,&a[m+i].y);
for(i=0;i<m;++i) scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].t);
std::sort(a,a+m,[&](const ky&p,const ky&q){return p.t<q.t;});
for(i=0;i<m;++i)
for(j=0;j<n+m;++j)
ds[i][j]=A(a[i].x-a[j].x)+A(a[i].y-a[j].y);
ct lim=1<<n;
for(s=0;s<lim;++s)
for(i=0;i<m+n;++i)
for(dis[s][i]=inf,j=0;j<n;++j)
if(s>>j&1) ckMin(dis[s][i],A(a[m+j].x-a[i].x)+A(a[m+j].y-a[i].y));
memset(f,63,sizeof(f)),memset(g,192,sizeof(g));
for(i=0;i<n;++i) f[1<<i][0]=0;
for(i=0;i<m;++i) g[0][i]=1;
for(s=0;s<lim;++s){
for(i=0;i<m;++i){
for(j=i;~j;--j)
if(f[s][j]+dis[s][i]<=a[i].t){ckMax(g[s][i],j+1);break;}
for(j=0;j<i;++j)
if(a[j].t+ds[j][i]<=a[i].t)
ckMax(g[s][i],g[s][j]+1);
if(g[s][i]<0) continue;
ckMin(f[s][g[s][i]],a[i].t);
for(j=0;j<n;++j)
if(!(s>>j&1))
ckMin(f[s|(1<<j)][g[s][i]],a[i].t+ds[i][m+j]);
}
for(i=0;i<=m;++i)
for(j=0;j<n;++j)
if(!(s>>j&1))
ckMin(f[s|(1<<j)][i],f[s][i]+dis[s][m+j]);
}
for(i=m;~i;--i)
for(s=0;s<lim;++s)
if(f[s][i]<inf)
return printf("%d",i),0;
return 0;
}
CF1523G (口胡,占坑)
发现 \(n\leq 5\times 10^4\) ,考虑一些数据结构。
我们发现 \(r_i-l_i+1=x\) 。
CF1517F (口胡)
不明白为什么 lxm 考场上没切这题。
感觉就是一个树形 dp ,可能有点麻烦,因为要分子树延伸和其他延伸。
设 \(f_{i,j}=i\) 子树内最深覆盖为 \(j\) , \(g_{i,j}=i\) 子树内还需要添加长度为 \(j\) 的链覆盖。做一个背包,两个数组之间互相转移即可。
CF1517G (口胡,占坑)
不明白为什么 lxm 考场上没切这题。
看到这种一堆限制的可以想网络流,拆点连边什么的。
JSOI2019 精准预测
鸽子竟然会更博!

