P1282 多米诺骨牌 (差值DP+背包)

题目描述

多米诺骨牌有上下2个方块组成，每个方块中有1~6个点。现有排成行的

上方块中点数之和记为S1，下方块中点数之和记为S2，它们的差为|S1-S2|。例如在图8-1中，S1=6+1+1+1=9，S2=1+5+3+2=11，|S1-S2|=2。每个多米诺骨牌可以旋转180°，使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。

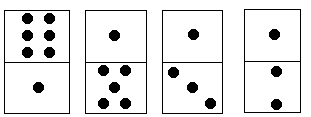
对于图中的例子，只要将最后一个多米诺骨牌旋转180°，可使上下2行点数之差为0。

输入输出格式

输入格式：

 

输入文件的第一行是一个正整数n(1≤n≤1000)，表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数a和b，且1≤a，b≤6。

 

输出格式：

 

输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

 

输入输出样例

输入样例#1：

4
6 1
1 5
1 3
1 2

输出样例#1:

1

Solution

此题是一道双向背包.

这道题一看,就觉得应该和背包有点关系.然后要想到背包的本质是什么.

背包的本质就是通过当前状态的前驱, 进行更新.

然后就是状态定义:

f[ i ][ j ] 表示 前 i 个组合里面 上面那个数组的和. 

同时因为无论怎么变化 两个数列的总和始终是不变的.

所以之后的状态转移方程和 背包非常相似.

可以试着自己想一想.

 

Ps: 注意 f[1][ ] 的初始化.

 

代码(内有一部分注释) :

#include<bits/stdc++.h>
using namespace std;
const int maxn=1008;
const int inf=1231654;
 int n,a[maxn],b[maxn];
 int w[maxn],sum;
 int f[maxn][6*maxn];
 //状态表示 前 i 个里面上一列的值是多少.
 //同时因为交换不会改变两列数的总和,所以可以很方便地求出另外一列的值
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&a[i],&b[i]);
        sum+=(a[i]+b[i]);
    }
    //表示 初始状态. 若第一个换就是 0 否则为1;
    for(int i=1;i<=n;i++)
    for(int j=0;j<=n*6+10;j++) f[i][j]=inf;
    f[1][a[1]]=0; f[1][b[1]]=1;
    for(int i=2;i<=n;i++)
    　　　// 注意从 2 开始
    for(int j=0;j<=n*6;j++)
    {
        if(j-a[i]>=0)
        f[i][j]=min(f[i][j], f[i-1][j-a[i]]);
        //若仍然为a 则不需要去加;
        if(j-b[i]>=0)
        f[i][j]=min(f[i][j], f[i-1][j-b[i]]+1);
    }
    int minc=inf,mint=inf;
    for(int i=1;i<=sum;i++)
    {
        if(f[n][i]!=inf)
        if(abs(i-(sum-i))<minc)
        minc=abs(i-(sum-i)),mint=f[n][i];else
        if(abs(i-(sum-i))==minc) mint=min(f[n][i],mint);
    }
    cout<<mint<<endl;
    return 0;
}