数据结构--堆
前言
在实际很多的应用场景中,我们对数据进行处理的时候,比如插入数据和删除数据时,我们常常需要快速的知道数据中最大值和最小值。而处理这种问题的方法之一,就是使用一个已经排序好的数据集合。通过这种方式,数据的最大值或最小值总是在数据集合的头部或者尾部(这取决于使用时升序排列还是降序排列)。然而,将数据集合继续有序排序需要代价是非常高的。并且在许多情况下,我们并不是相对数据集合所有的元素进行排序,可能我能只是希望可以快速的找数据集合中的最大值或者最小值而已,只需要让元素排序在原本的储存位置就行。堆和优先队列这种结构便是可以处理这种问题的有效方法。
堆的描述
堆的本质是一颗二叉树,通常其子结点存储的值比父结点存储的值小。所以,根结点是树中最大的结点。同样,我们也可以让堆有另外一种形式,即子结点储存值都比父结点存储的值来的大。这样根结点就是树种最小的值。这样的规则,让二叉树在局部是有序的,任何一个结点和其兄弟结点之间没有必然的大小关系,但是和它的父结点有必然的大小关系。如果子结点比父结点值小,我们称这种结构为最大堆,反之子结点比父结点大为最小堆。
堆的本质是二叉树,随着结点的增加,树会逐级从左向右增长。因此对于堆而言,一个比较好的表示左平衡树的方式,将结点通过水平遍历的方式放置在一个数组中。这样对于一个数组中处于位置\(i\)的结点,其父结点位于\(|i-1|/2\)的位置,计算的时候要忽略\(|i-1|/2\)的小数点部分。其左结点和右结点分别位于\(2i+1\)和\(2i+2\)的位置。这样的结构对于堆是十分重要的,因为可以快速的定位堆的最后一个结点位置。最后一个结点就表示位于树的最深处的最右边的结点。这个在实现堆的某些操作的时候是很重要的。为了方便理解,我这里画了一幅图来进行说明。
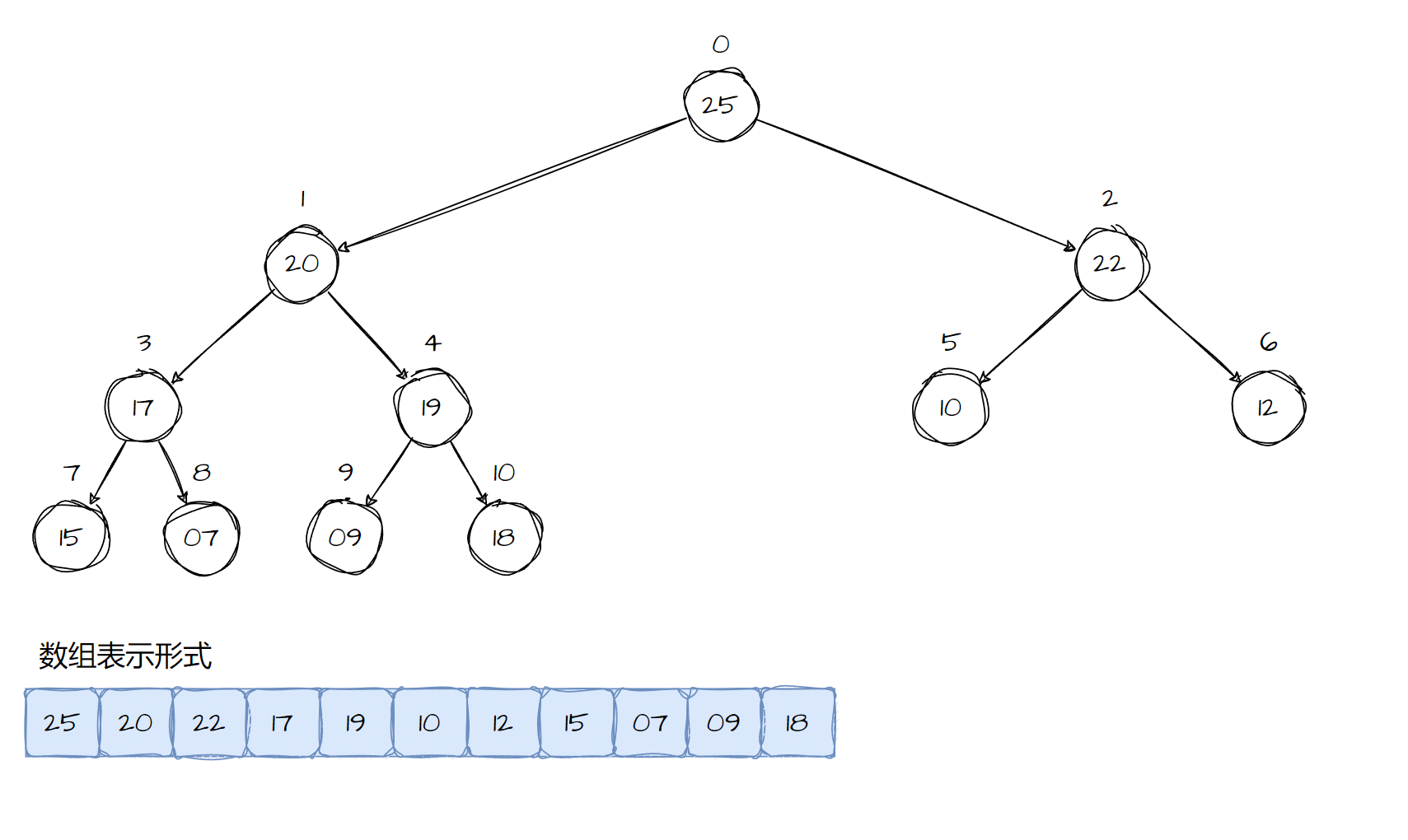
堆的接口定义
heap_init
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
函数原型:void heap_init(Heap* heap, int);
返回值: 无
函数说明: 初始化堆heap。在对堆进行其他的操作前必须先调用当前函数对堆进行初始化。在堆进行初始化的过程中主要做这几个行为。
- 将heap的成员size设置为0
- 将heap的成员函数destroy指向你给予的摧毁函数
- 将heap的tree指针设置为NULL
时间复杂度:heap_init的时间复杂度为\(O(1)\) 因为初始化堆的几个步骤在固定的几个时间完成。
heap_destroy
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
函数原型:void heap_destroy(heap_t *heap);
返回值: 无
函数说明: 摧毁堆heap,该函数的主要作用是移除堆中的所有的结点。当heap结构中的指针不为NULL时,destroy将使用指向的函数对堆的结点进行移除。
时间复杂度:heap_destroy函数的时间复杂度为\(O(N)\),这是由于必须遍历所有堆中的所有的结点。当然如果堆的destroy函数为NULL。时间复杂度为\(O(1)\)
heap_Insert
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
函数原型:int heap_insert(heap_t *heap, const void *data);
返回值: 如果函数插入成功返回0,否则返回-1
函数说明: 将heap中插入一个结点。新的结点包含一个指向data的指针,只要结点存在于堆中,这个指针便一直存在。和data相关的内存空间给函数的使用进行调用。
时间复杂度:时间复杂度为\(O(lgN)\),其中N为堆的结点
heap_extract
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
函数原型:int heap_extract(heap_t *heap, void **data);
返回值: 如果函数释放成功返回0,否则返回-1
函数说明: 从堆heap中释放顶点的结点
时间复杂度:时间复杂度为\(O(lgN)\),其中N为堆的结点
以上为我们声明堆的结点,现在要分析堆的实现方案,只有知道堆的实现方案,我们才可以开始进行堆的C语言代码的实现。
堆的接口实现原理
堆的插入heap_Insert
堆使用heap_insert函数进行结点的插入。函数将新结点加入到用户指定的堆中,首先我们需要对新的结点进行内存的分配,保证树可以容纳这个结点。将新插入的结点放在数组的末尾。这个时候插入数据会破坏堆的排序规则,所以我们必须调节树的结构,对结点进行重新排序.
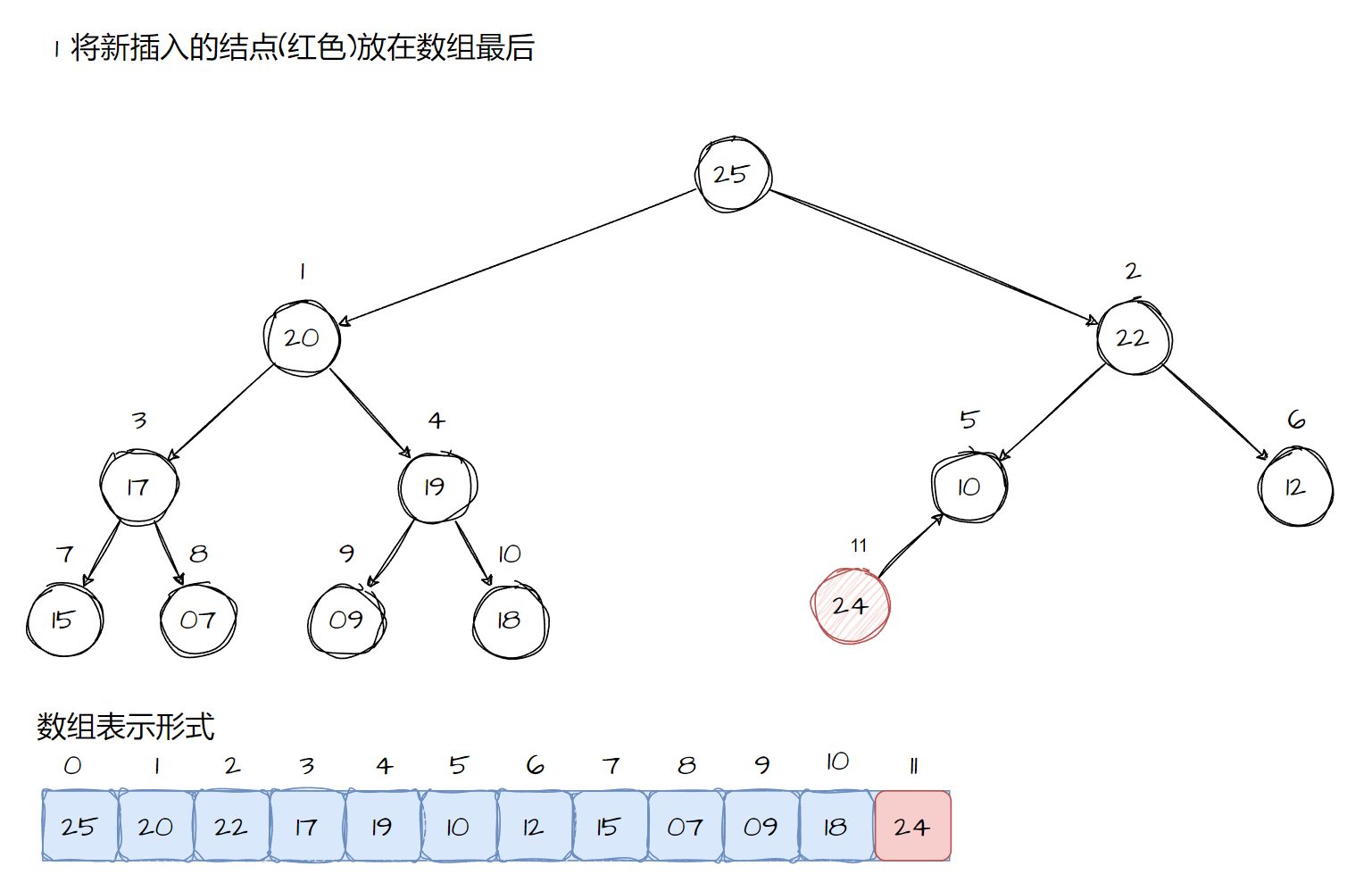
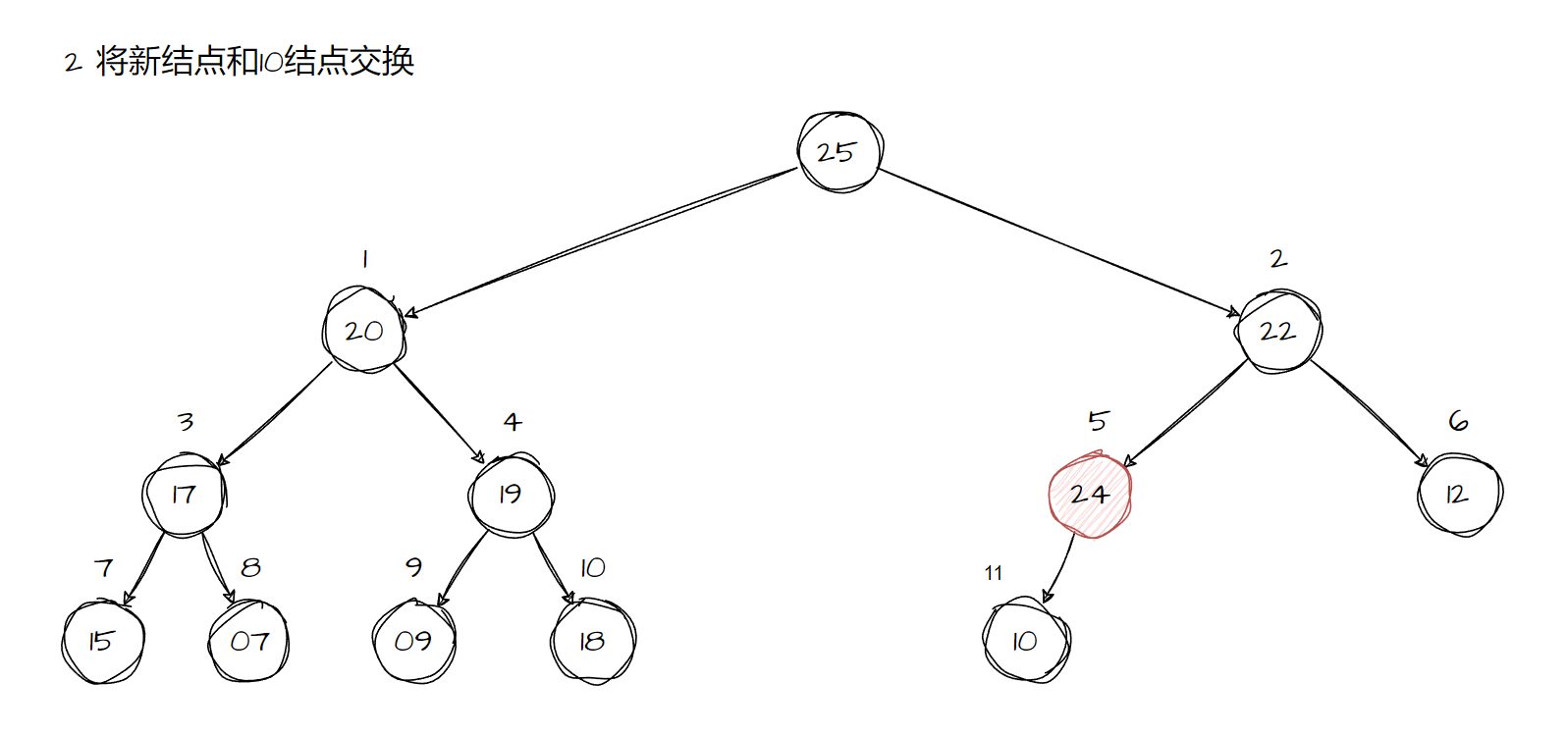
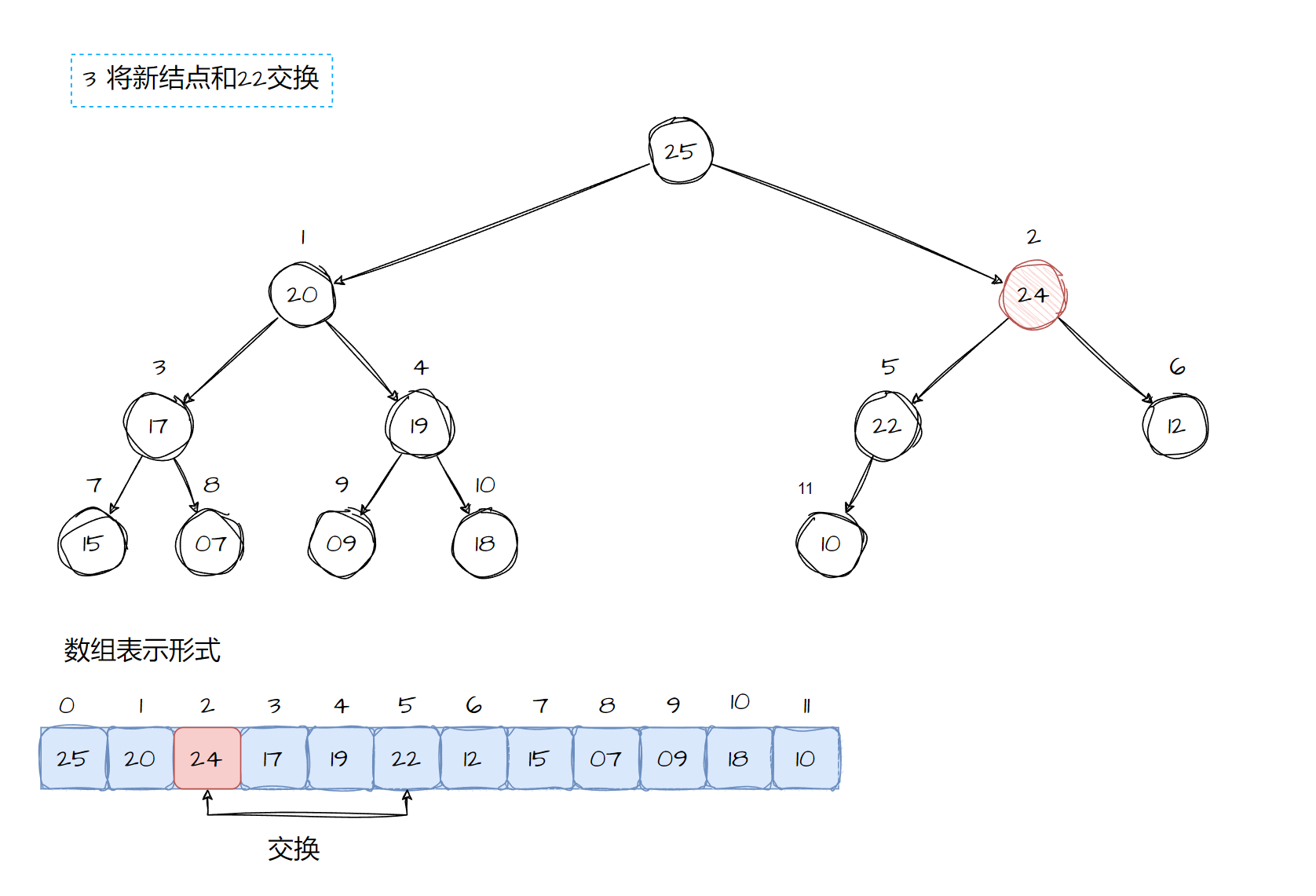
在插入结点时,为了重新的排序一颗树,只需要考虑新的结点插入的是那个分支,因为这是形成堆的局部的开始分支。从新结点开始,将结点向树的上方层层移动,比较每个子结点和它的父结点。在每一层上,如果父结点和子结点的位置不正确,就交换两个结点的内容。这个交换的结果会不断的进行直到某一层满足了堆的规则为止。最后要堆的size进行更新。
堆的插入过程的时间复杂度为\(O(lgN)\),这是因为在最糟糕的情况下,需要将新的结点中的内容从树的最底层移动到树的顶层,这个是一个\(lgN\)级别的遍历过程。
堆的顶部释放heap_extract
堆有heap_extracy函数来对堆的顶部元素进行释放,首先,将data指向要释放的结点的数据进行释放。接下去,保存最后一个结点的内容,并且将二叉树的大小减去一,将树的大小减去1,为树分配较小的内存空间。完成以上工作后,我们将最后一个结点的内容拷到根结点中。显然,这个过程会破坏堆的固有大小规则,所以我们必须重新的调节堆的结构。
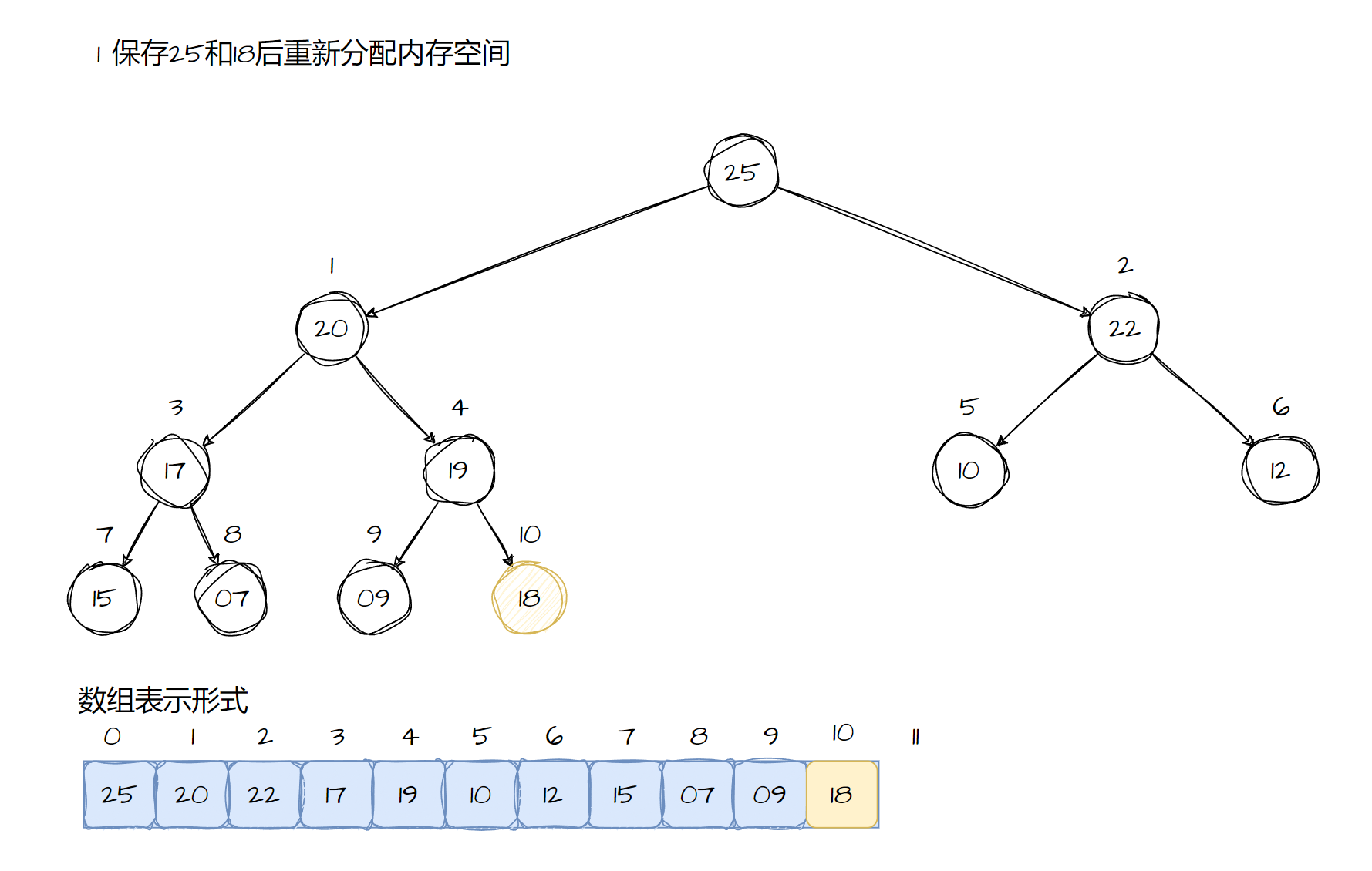
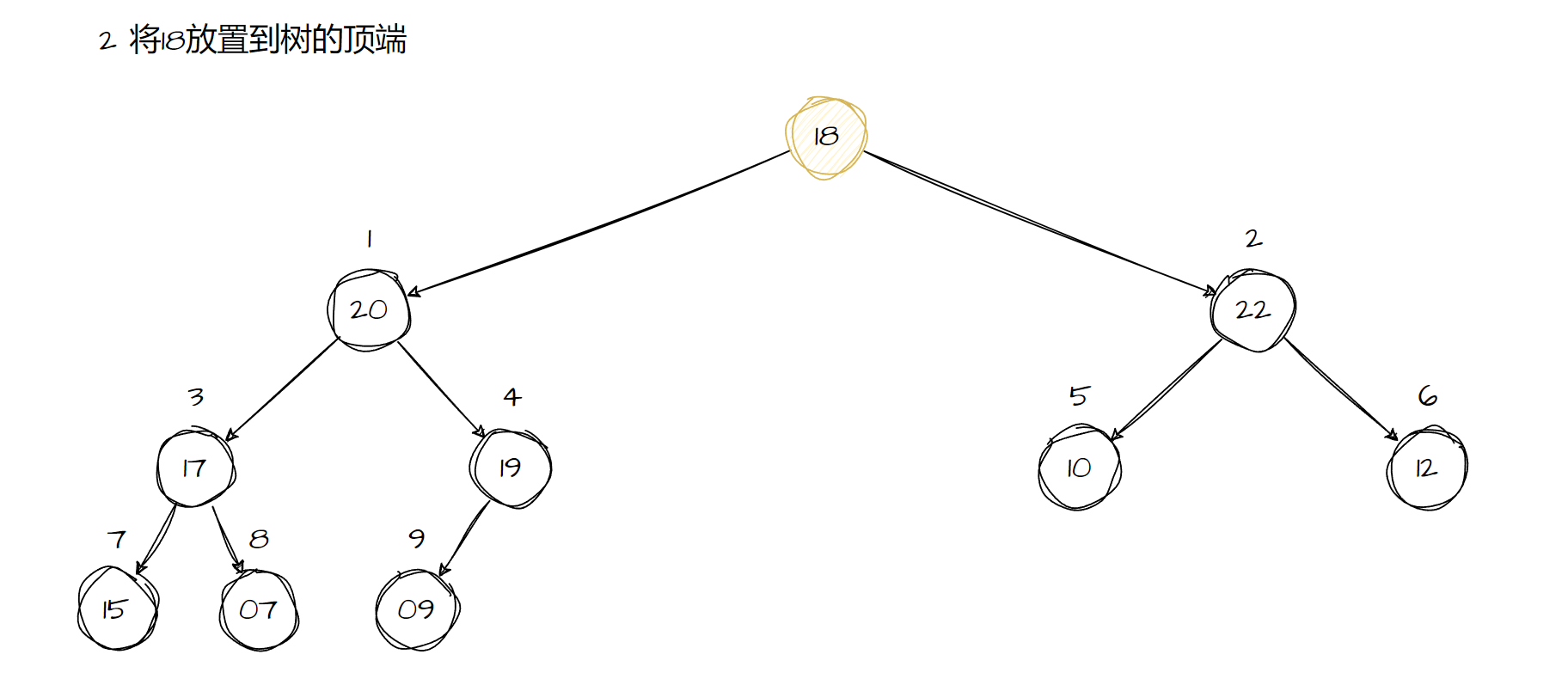
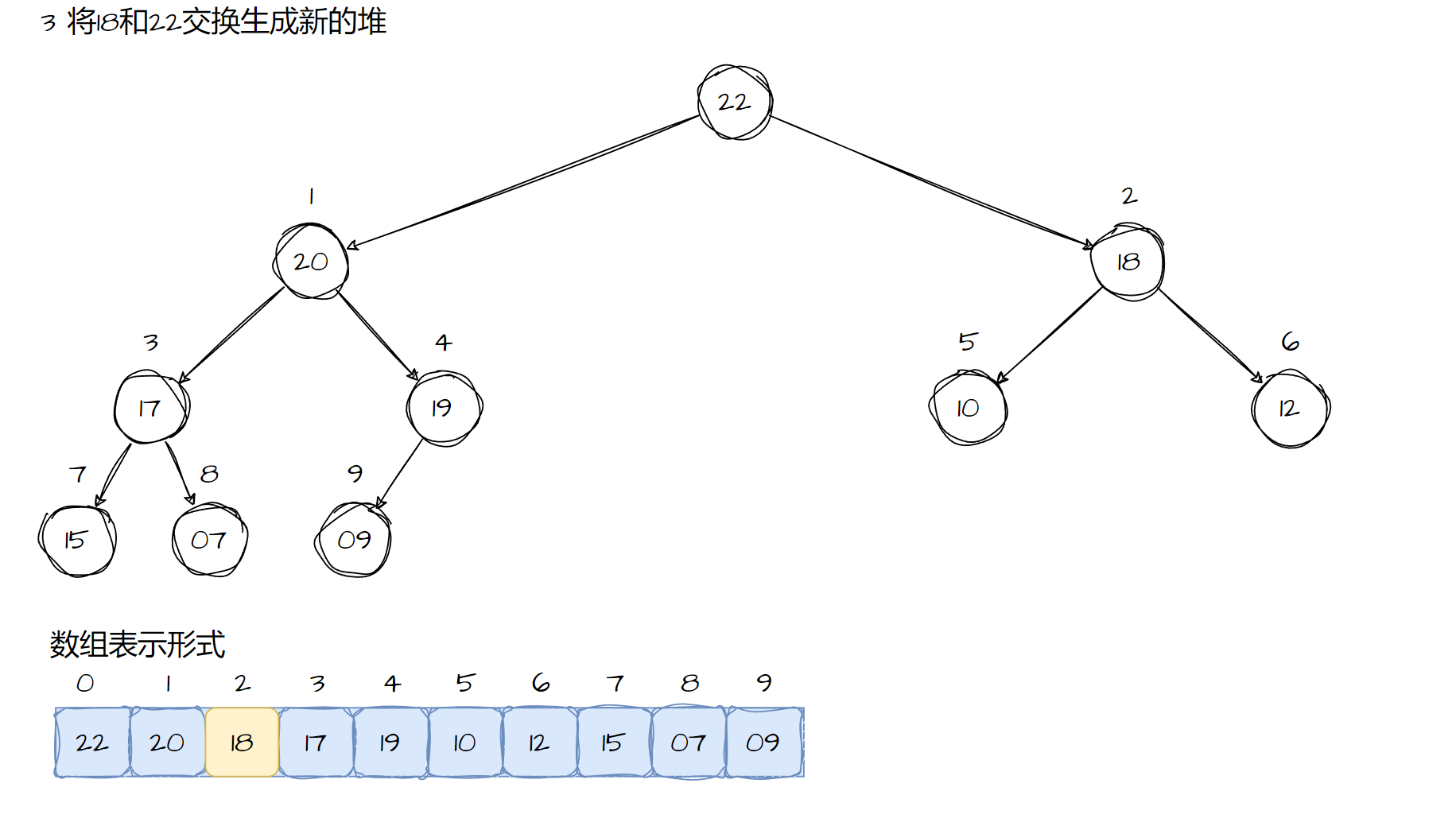
实现代码
实现的代码以上为原理进行C语言编写
#ifndef __HEAP_H__
#define __HEAP_H__
/***************************************************************************************
* 定义堆的结构体
***************************************************************************************/
typedef struct __heap
{
int size;
int (*compare)(const void *key1, const void *key2);
void (*destroy)(void *data);
void **tree;
}heap_t;
/***************************************************************************************
* 堆的公共接口
***************************************************************************************/
void heap_init(heap_t *heap, int (*compare)(const void *key1, const void *key2), void (*destroy)(void *data));
void heap_destroy(heap_t *heap);
int heap_insert(heap_t *heap, const void *data);
int heap_extract(heap_t *heap, void **data);
#define HEAD_SIZE(__heap) ((__heap)->size)
#endif /* heap.h */
#include <stdlib.h>
#include <string.h>
#include "heap.h"
#define HEAP_PARENT(__npos) ((int)(((__npos)-1)) / 2)
#define HEAP_LEFT(__npos) ((int)(((__npos)*2)) + 1)
#define HEAP_RIGHT(__npos) ((int)(((__npos)*2)) + 2)
void heap_init(heap_t *heap, int (*compare)(const void *key1, const void *key2), void (*destroy)(void *data))
{
/* 初始化堆 */
heap->size = 0;
heap->compare = compare;
heap->destroy = destroy;
heap->tree = NULL;
return;
}
void heap_destroy(heap_t *heap)
{
/* 从堆中将所有的结点移除 */
if(heap->tree != NULL)
{
for(int i = 0; i < HEAD_SIZE(heap); ++i)
{
heap->destroy(heap->tree[i]);
}
}
/* 释放堆的分配内存 */
free(heap->tree);
memset(heap, 0, sizeof(heap_t));
return;
}
int heap_insert(heap_t *heap, const void *data)
{
void *temp;
int ipos;
int ppos;
if((temp = (void**)realloc(heap->tree, (HEAD_SIZE(heap)+1)*sizeof(void*))) == NULL)
{
return -1;
}
else
{
heap->tree = temp;
}
/* 在后结点插入结点 */
heap->tree[HEAD_SIZE(heap)] = (void*)data;
ipos = HEAD_SIZE(heap);
ppos = HEAP_PARENT(ipos);
while (ipos > 0 && heap->compare(heap->tree[ppos], heap->tree[ipos]) < 0)
{
temp = heap->tree[ppos];
heap->tree[ppos] = heap->tree[ipos];
heap->tree[ipos] = temp;
ipos = ppos;
ppos = HEAP_PARENT(ipos);
}
heap->size++;
return 0;
}
int heap_extract(heap_t *heap, void **data)
{
void *save;
void *temp;
int ipos;
int lpos;
int rpos;
int mpos;
if(HEAD_SIZE(heap) == 0)
return -1;
*data = heap->tree[0];
save = heap->tree[HEAD_SIZE(heap) - 1];
if((HEAD_SIZE(heap) - 1) > 0)
{
if((temp == (void**)realloc(heap->tree, (HEAD_SIZE(heap) - 1) * sizeof(void*))) == NULL)
return -1;
else
heap->tree = temp;
heap->size--;
}
else
{
free(heap->tree);
heap->tree = NULL;
heap->size = 0;
return 0;
}
heap->tree[0] = save;
ipos = 0;
lpos = HEAP_LEFT(ipos);
rpos = HEAP_RIGHT(ipos);
while (1)
{
lpos = HEAP_LEFT(ipos);
rpos = HEAP_RIGHT(ipos);
if(lpos < HEAD_SIZE(heap) && heap->compare(heap->tree[lpos], heap->tree[ipos]) > 0)
mpos = lpos;
else
mpos = ipos;
if(rpos < HEAD_SIZE(heap) && heap->compare(heap->tree[rpos], heap->tree[mpos]) > 0)
mpos = rpos;
if(mpos == ipos)
break;
else
{
temp = heap->tree[mpos];
heap->tree[mpos] = heap->tree[ipos];
heap->tree[ipos] = temp;
ipos = mpos;
}
}
return 0;
}


