数据结构--树
前言
树其实这个数据结构在生活种比比皆是,比如家族的族谱,比赛的对战顺序或者自然界当中的看的见的花草树木的根茎。在计算机中,树由称为结点的元素按照层次结构的方式组织而成,层次最顶端称之为根,与根直连接称之为根的子节点,通常子结点的本身也有属于它们自己的子节点,除了根结点外,这个体系结构每一个结点都有唯一的父结点,也就是说只有唯一的与之相连接的上级结点,一个结点拥有多少个子节点取决树的类型,这个量值我们称树的分支因子,它决定了当插入结点时树的分支的扩展的速度。
本文章讨论二叉树,这是一种简单且功能强大的树,树的分支因子值为2。并且在讨论二叉树本文章也会讨论二叉搜索树,这一种专门用于查找操作的二叉树。
二叉树的介绍
二叉树是一种将结点按照树型的层次结构组织起来的数据结构,每一个结点最多只有两个与它相连接的子节点。直接连接在结点下方的结点我们称之为子结点,而直接连接的上级结点我们称之为父结点。结点也可以拥有兄弟,祖先和子孙。类似我们族谱的关系,一个结点的兄弟结点时其父结点的其他子节点,一个结点的子孙结点是其下级的所有结点。而祖先结点是其和根结点路径上的所有结点。为了方便理解我们可以使用下图进行理解。
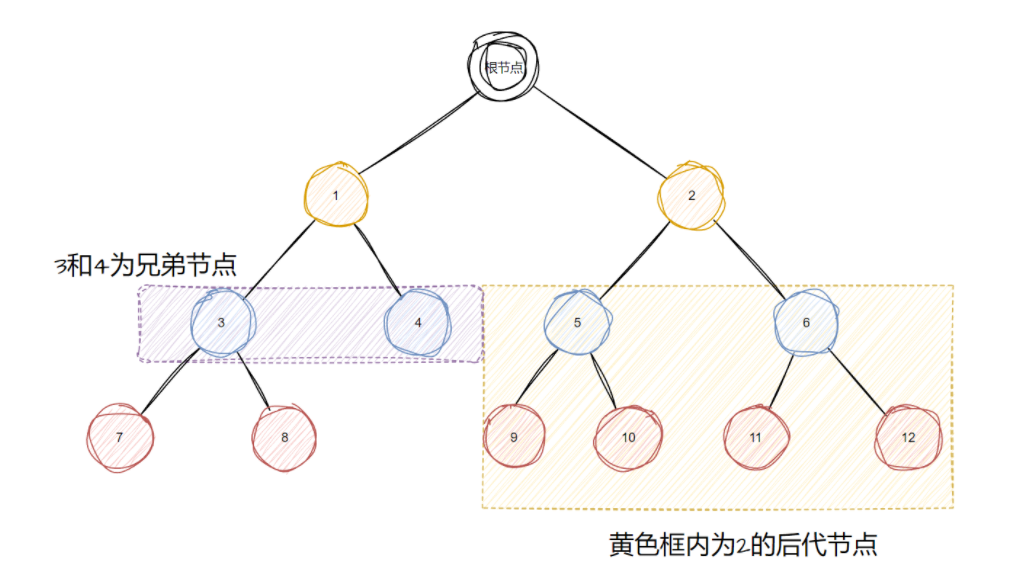
从上图我们可以总结出一个结点的特征,每个结点都用三个部分组成,一个数据成员和两个左右指针。通过这三个成员的结构体,将每一个结点的左右指针分别指向该结点的子节点,通过这种方式便可以构建一颗二叉树,如果某个结点没有子结点,就将相应的指针设置为NULL。这就可以表示当前结点为叶接点是一个分支的结束、叶子结点是一棵树的边缘,且没有子节点。当有时候我们一次要处理多颗树时,把这些树组成的集合称之为森林。我们把上图树的模型转变为C语言的树模型如下图所示。
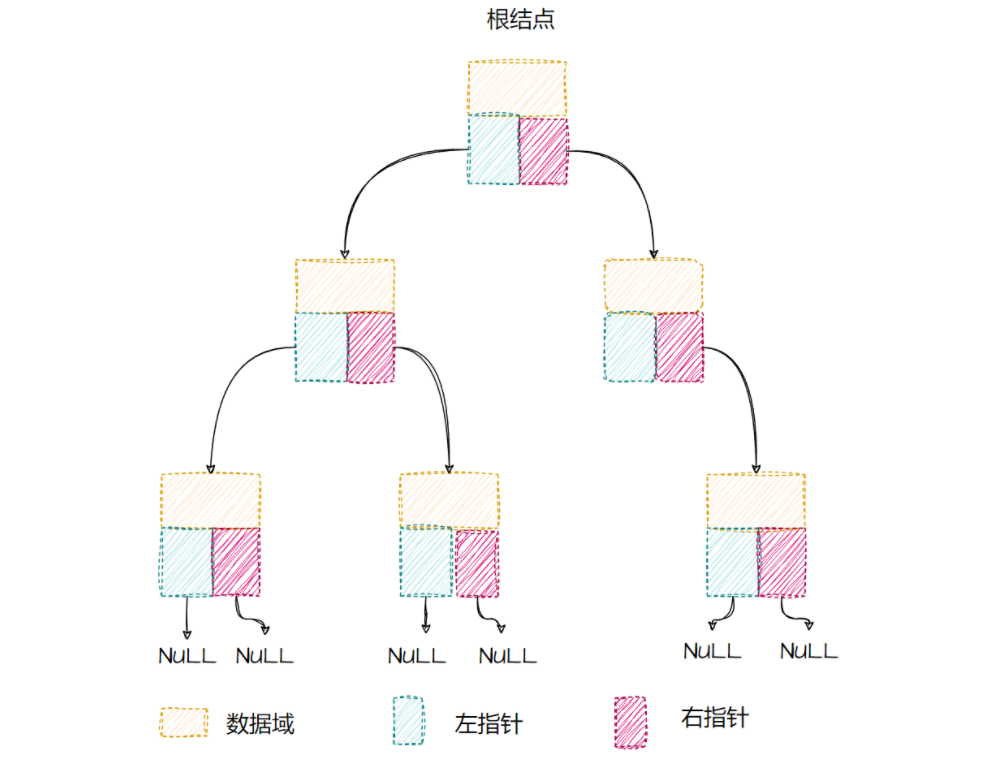
树的周游算法
周游一颗二叉树表示按照某种规定的是顺序来依次访问树的每一个结点。同其他链式的数据结构相比较(比如链表),如何遍历一颗二叉树的结点的方式可能不是很明显,事实上,我们可以采用多种方式来进行树的周游。一般而言,我们会采用四种树的周游算法:先序遍历、中序遍历、后序遍历以及层级遍历。
如果我们引入递归的思维,将一颗树想象为许多更小的树的子集合,那么遍历一颗树就变得相当的简单。
先序遍历
对于一颗树,按照先序遍历的方式,我们首先先访问它的根结点、然后是左子节点,最后是右子节点。由于先序遍历是从左到右遍历各个子树,因此以相同的方式将左子节点和右子节点当做新的子树的根节点就可以通过递归的思维完成先序遍历。
中序遍历
对于一颗树,按照中序遍历的方式,首先先访问左子节点,然后是根结点,最后才是右子节点,由于按照是顺序是从左到右的方式来遍历各个子树,因此以相同的方式将左子节点和右子节点当做新的子树的根。
后序遍历
对于一颗树,按照后序遍历的方式,首先先访问左子节点然后是右子节点,最后才是根结点,由于按照是顺序是从左到右的方式来遍历各个子树,因此以相同的方式将左子节点和右子节点当做新的子树的根。
层级遍历
采用层级遍历的方式来周游一棵树,首先访问树的根,然后向下层处理,按照从左到右的顺序访问每层的结点。层级遍历运用广度优先的策略。后续会开一个章节专门说明广度优先和深度优先的思维。
假设存在一颗树的结构如下:

那么对与这棵树使用不同周游算法访问的顺序是不一样,如下图所示
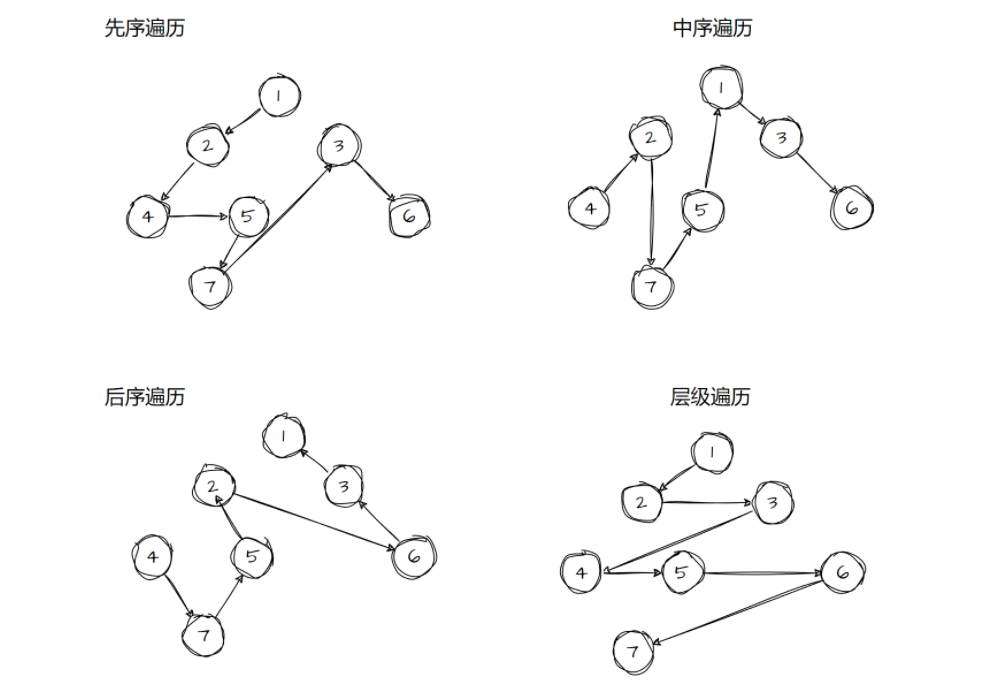
树的平衡
树的平衡,树的平衡是指在给定结点的数量时,要保证树的高度尽可能的短。这就意味了结点在加入下一层之前必须保证本层的结点是足够满的。换句话说就是树的叶子结点都是在同一层或者叶子结点在最后两层,且倒数第二层是满的。那么可以称这颗树是平衡的。对与平衡树的应用,在后续我会开一章节来进行说明,目前只要知道平衡树这个概念。
例如以下就是一个平衡树
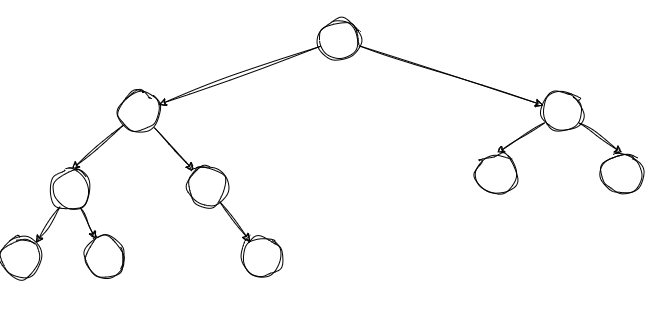
二叉树的接口定义
#ifndef __BITREE_H__
#define __BITREE_H__
#include <stdio.h>
/*************************************************************
* 二叉树结点结构体
*************************************************************/
typedef struct __bitree_node
{
void *data;
struct __bitree_node *left;
struct __bitree_node *right;
}bitree_node_t;
/*************************************************************
* 二叉树结构体
*************************************************************/
typedef struct __bitree
{
int size;
int (*compare)(const void *key1, const void *key2);
void (*destroy)(void *data);
bitree_node_t *root;
}bitree_t;
/*************************************************************
* 二叉树函数接口
*************************************************************/
/* 二叉树初始化 */
void bitree_init(bitree_t* tree, void (*destroy)(void *data));
/* 二叉树析构 */
void bitree_destroy(bitree_t* tree);
/* 二叉树左插 */
int bitree_ins_left(bitree_t* tree, bitree_node_t* node, const void *data);
/* 二叉树右插 */
int bitree_ins_right(bitree_t* tree, bitree_node_t* node, const void *data);
/* 二叉树左结点去除 */
void bitree_rem_left(bitree_t* tree, bitree_node_t* node);
/* 二叉树右结点去除 */
void bitree_rem_right(bitree_t* tree, bitree_node_t* node);
/* 二叉树合并 */
int bitree_rem_merge(bitree_t* merge, bitree_t* left, bitree_t *right, const void *data);
/*************************************************************
* 宏定义
*************************************************************/
#define BITREE_SIZE(__tree) ((__tree->size))
#define BITREE_ROOT(__tree) ((__tree->root))
#define BITREE_IS_ENB(__node) ((__node == NULL))
#define BITREE_IS_LEAF(__node) ((__node->left == NULL) && (__node->right == NULL))
#define BITREE_DATA(__node) ((__node->data))
#define BITREE_LEFT(__node) ((__node->left))
#define BITREE_RIGHT(__node) ((__node->right))
#endif /* bitree.h */
二叉树的接口实现
#include "bitree.h"
#include <stdlib.h>
#include <string.h>
void bitree_init(bitree_t* tree, void (*destroy)(void *data))
{
/*1 对二叉树进行初始化 */
tree->size = 0;
tree->destroy = destroy;
tree->root = NULL;
return;
}
void bitree_destroy(bitree_t* tree)
{
/* 将所有结点移除 */
bitree_rem_left(tree, NULL);
memset(tree, 0x00, sizeof(bitree_t));
return;
}
int bitree_ins_left(bitree_t* tree, bitree_node_t* node, const void *data)
{
bitree_node_t *new_node;
bitree_node_t **position;
/* 如果node == NULL,则插入根节点,在插入根节点前要保证树是空的 */
if(node == NULL)
{
if(BITREE_SIZE(tree) > 0)
{
return -1;
}
position = &tree->root;
}
else
{
if(BITREE_LEFT(node) != NULL)
{
return -1;
}
position = &node->left;
}
if((new_node = (bitree_node_t*)malloc(sizeof(bitree_node_t))) == NULL)
{
return -1;
}
new_node->data = (void*)data;
new_node->left = NULL;
new_node->right = NULL;
*position = new_node;
tree->size++;
return 0;
}
/* 二叉树右插 */
int bitree_ins_right(bitree_t* tree, bitree_node_t* node, const void *data)
{
bitree_node_t* new_node;
bitree_node_t** position;
/* 如果node == NULL,则插入根节点,在插入根节点前要保证树是空的 */
if (node == NULL)
{
if (BITREE_SIZE(tree) > 0)
{
return -1;
}
position = &tree->root;
}
else
{
if (BITREE_LEFT(node) != NULL)
{
return -1;
}
position = &node->right;
}
if ((new_node = (bitree_node_t*)malloc(sizeof(bitree_node_t))) == NULL)
{
return -1;
}
new_node->data = (void*)data;
new_node->left = NULL;
new_node->right = NULL;
*position = new_node;
tree->size++;
return 0;
}
/* 二叉树左结点去除 */
void bitree_rem_left(bitree_t* tree, bitree_node_t* node)
{
bitree_node_t **position;
if(BITREE_SIZE(tree) == 0)
{
return;
}
if(node == NULL)
{
position = &tree->root;
}
else
{
position = &node->left;
}
if(*position != NULL)
{
bitree_rem_left(tree, *position);
bitree_rem_right(tree, *position);
if(tree->destroy != NULL)
{
tree->destroy((*position)->data);
}
free(*position);
*position = NULL;
tree->size--;
}
}
// /* 二叉树右结点去除 */
void bitree_rem_right(bitree_t* tree, bitree_node_t* node)
{
bitree_node_t **position;
if(BITREE_SIZE(tree) == 0)
{
return;
}
if(node == NULL)
{
position = &tree->root;
}
else
{
position = &node->right;
}
if(*position != NULL)
{
bitree_rem_left(tree, *position);
bitree_rem_right(tree, *position);
if(tree->destroy != NULL)
{
tree->destroy((*position)->data);
}
free(*position);
*position = NULL;
tree->size--;
}
}
// /* 二叉树合并 */
int bitree_rem_merge(bitree_t* merge, bitree_t* left, bitree_t *right, const void *data)
{
bitree_init(merge, left->destroy);
if(bitree_ins_left(merge, NULL, data) != 0)
{
bitree_destroy(merge);
return -1;
}
BITREE_ROOT(merge)->left = BITREE_ROOT(left);
BITREE_ROOT(merge)->right = BITREE_ROOT(right);
merge->size = merge->size + BITREE_SIZE(left) + BITREE_SIZE(right);
left->root = NULL;
left->size = 0;
right->root = NULL;
right->size = 0;
return 0;
}
代码实现分析
待续
二叉搜索树的介绍
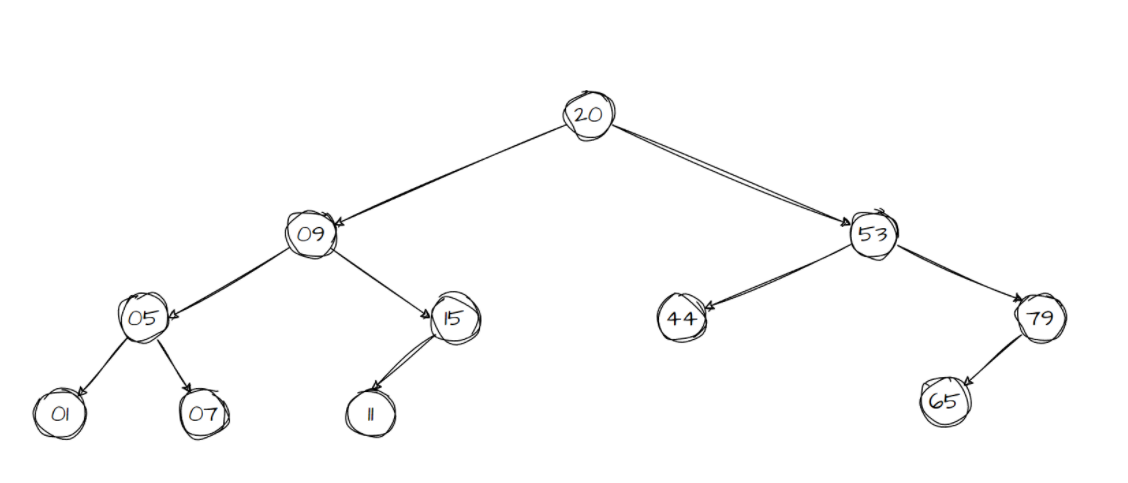
二叉搜索树是由二叉树组成的专门用于查找和搜索为目的一种数据结构。要在二叉树中查询一个结点,从根结点开始一层一层向下遍历,直到找到目标为止。当遇到一个比目标结点的值大的结点时,顺着该结点的左子树进行查找,如果遇到的结点的值小于目标结点,则顺着该结点的右子树继续查找。为了可以更好了解二叉树的查找流程,这里我利用一个例子来进行说明,如下图所示。
如果我们有一个任务是要找到值为15的结点位置,从根结点开始进行寻找,因为15小于20,所以寻找的方向为根结点的左子节点,又因为15比09大,所以寻找09结点的右子节点,此时的值正好为15我们就找到了目标结点。注意的一点时,如果到达了树的分支结点尽头依然没有找到目标结点,则说明目标结点并不在树中。
当然,敏锐的朋友应该意识到了,搜索一颗二叉树过程依赖其结点的插入方式都是按照类似的方式进行插入。因此要插入一个结点,还是从根结点开始,例如我要插入一个结点,结点的值为65,对于根结点,因为65比20要大。所以移动到右子节点,然后65又比53大,所以哦移动到53结点的右字节点,又因为65比79小,所以移动到79结点的左子节点,最后由于到了树的尽头,所以65的插入的位置就是79的左子节点上。这里有一个注意点就是重复的结点不允许出现。
二叉搜索树是一种用于的查找操作的高效的数据结构,因为在最坏的情况下,只需要查找一个分支的数据就可以,而不用检索所有的数据。因此,查找操作的时间的复杂度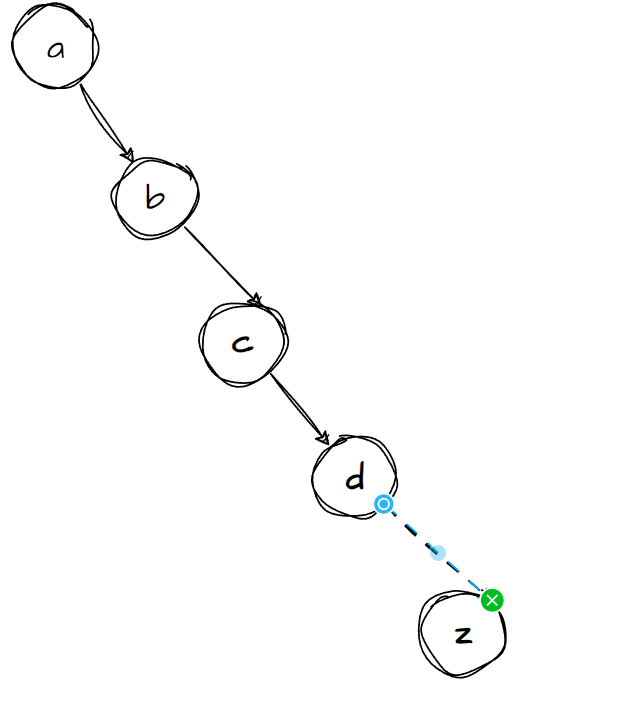
在上图只存在一个分支,树处于最不平衡的状态,这样若要找到z这个单词的结点就必须索引之前的所有结点,这样的速度是十分慢的。但是通常而言我们插入结点和移除结点的顺序是不能够控制,所有我们必须采取一些积极的方式来保证树的平衡。
二叉搜索树的实现和分析
在之前的进行了二叉搜索树的分析提到,只有当前二叉搜索树是保持是平衡时候,我们的搜索的效率才会提高。但是保持一颗树的平衡,实际上并不是那么简单,但是我们有一些的成熟的方法或者说策略可以使用,其中一种方式便是将二叉搜索树实现为AVL树。
AVL树(Adel'son -Vel'skii and Landis)是一种特殊的二叉树,它的每一个结点都保存一份额外的信息:结点的平衡因子是它的右子树高度减去它的左子树的高度。每次我们插入结点时,AVL树都需要自我进行调节,使得所有的结点的平衡因子保持为+1、-1和0。当子树的根节点+1时,树是左倾斜的,当一颗树的平衡结点为-1时,它时右倾斜。一颗子树的根结点的平衡因子就代表了子树的平衡性,所有的子树几乎保持在平衡状态,这么一来AVL树在总体上就基本说是保持平衡的。AVL平衡树的例子,每一个结点上面的数字表示平衡因子。
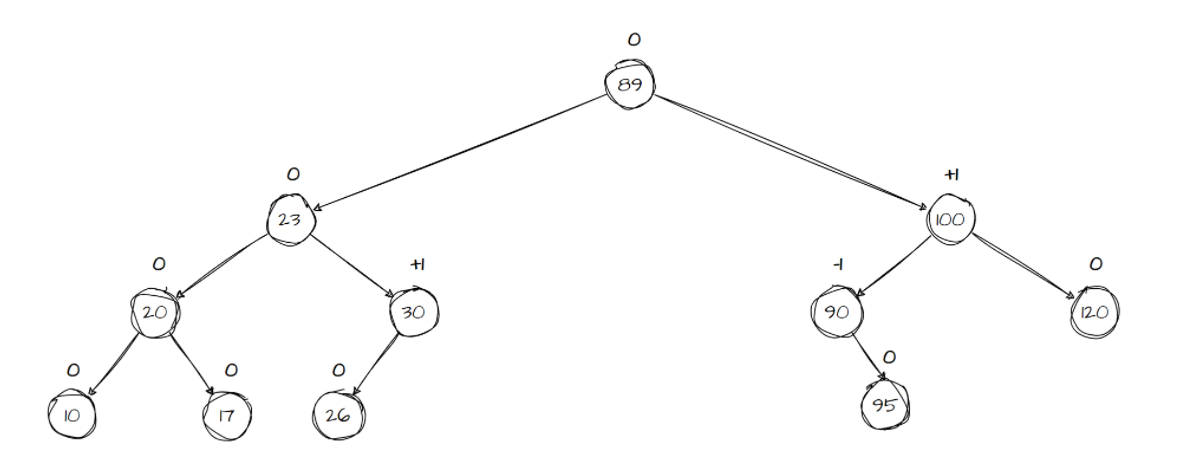
AVL树的基本查找和插入和之前的写过的二叉树是一样,但是AVL树在插入一个新的结点,还有一些额外的工作需要进行的操作。首先必须计算插入的新的结点对平衡结点造成的影响,这一点是很自然的,毕竟AVL树进行要保证树尽量的处于平衡状态。可以把操作总结为以下两个步骤:
- 重新计算因为插入操作造成了平衡因子的改变
- 如果有结点的平衡因子变成了+2或者-2,就必须从这个结点重新平衡这棵树,这个重新的平衡就被称为旋转
AVL树的旋转
旋转操作是用来的平衡AVL树的某一部分。通过重新对结点进行排序,同时保持结点和结点之间的关系,依然是左子节点小于父结点,父结点小于右子节点,即旋转后树依然是一颗二叉搜索树,并且在旋转后,旋转子树中的所有的结点的平衡因子都是+1,0,-1。
按照旋转的方向,存在四种旋转类型操作需要执行。分别是LL(left-left)、LR(left-right)、RR(right-right)和RL(right-left)旋转。为了可以行形象的理解在插入结点时需要执行哪一种旋转类型,我们假设插入的结点为x,并且假设A为离x最近且平衡因子为+2或者-2的祖先,那么我们可以归纳以下四种情况进行处理。
LL旋转
当x位于A的左子树的左子树上时,执行LL操作。设left为A的左子树,要执行LL旋转操作,将A的左指针指向left的右子结点,left的右子结点指向A,将原来指向A的指针指向left。
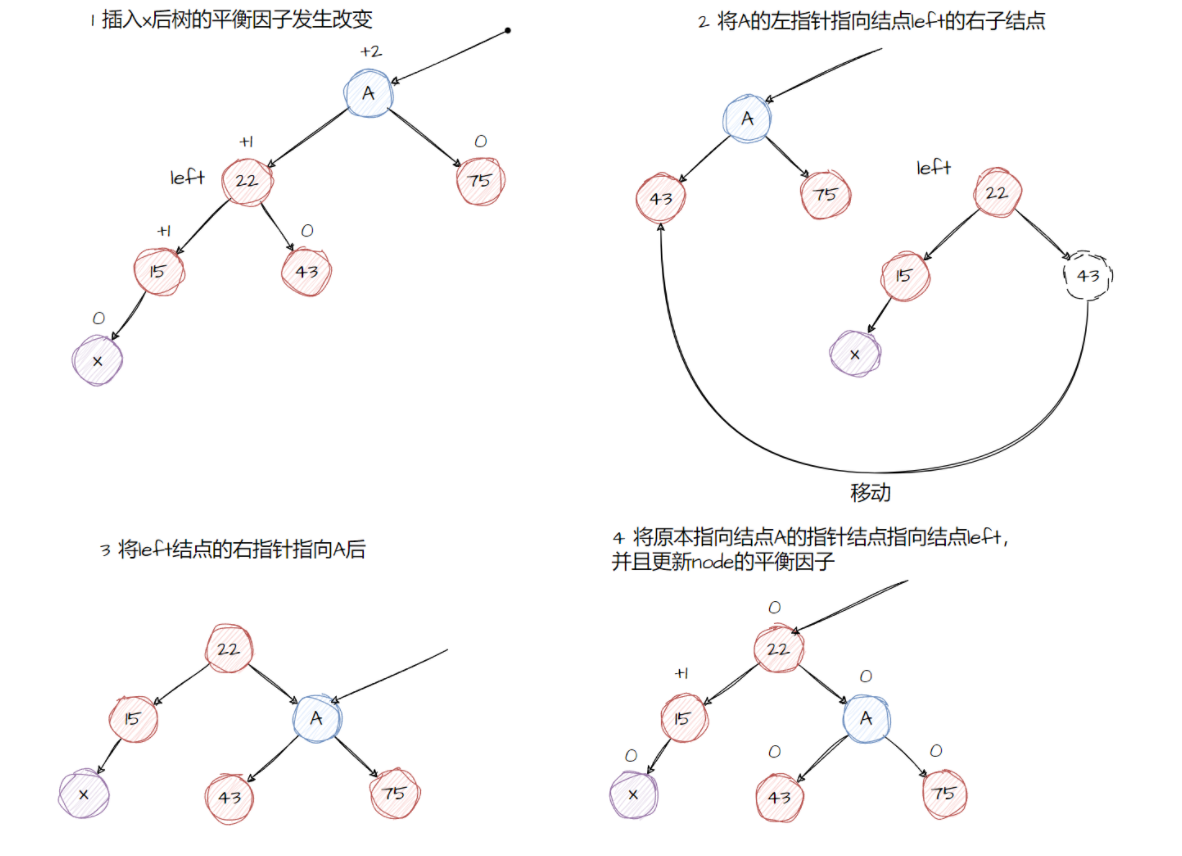
LR旋转
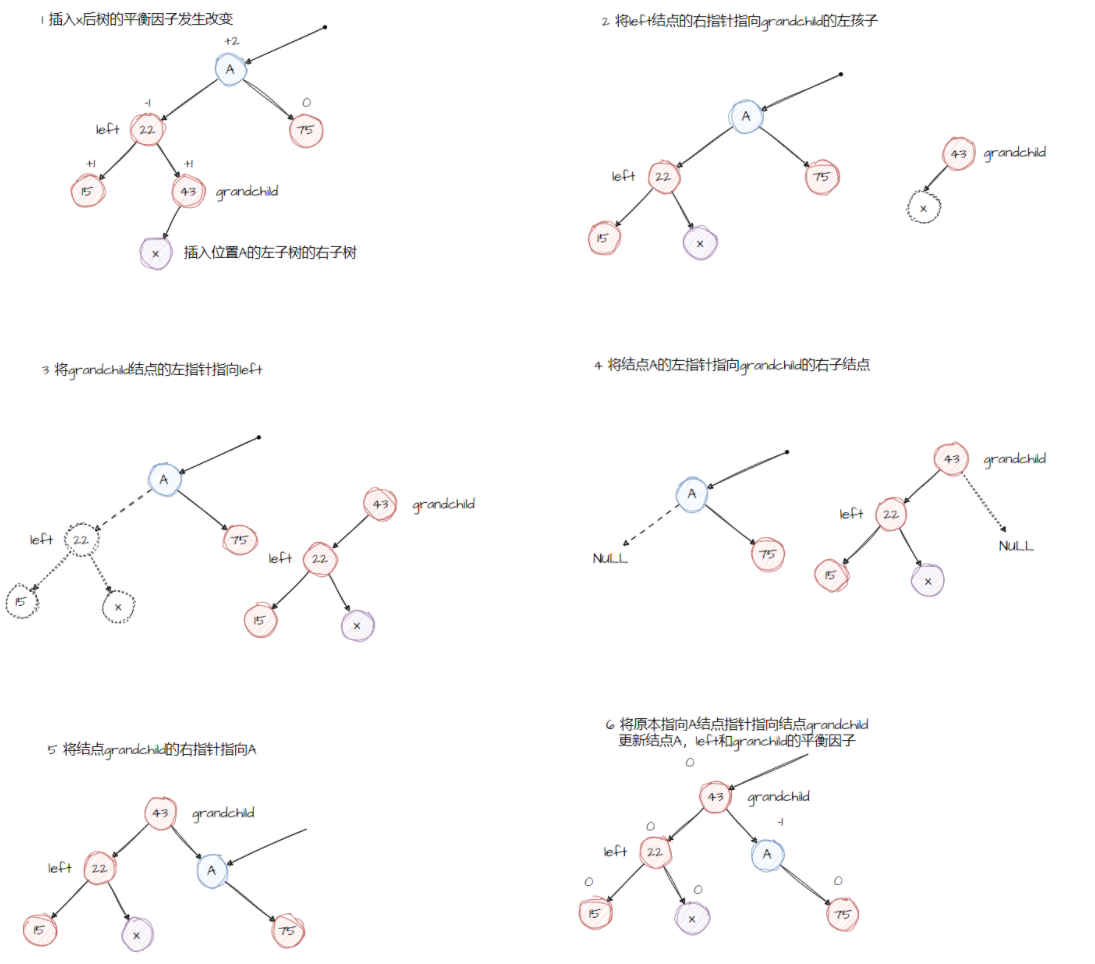
当x的位于A结点左子树的右结点上时,执行LR旋转操作。设left的为A的左子节点,并且设A的子孙结点为grandchild为left右子节点。要执行LR旋转,将left的右子结点指向grandchild的左子结点,grandchild的左子节点指向left,A的左子结点指向grandchild的右子结点,再将grandchild的左子结点指向grandchild的右子结点,再将grandchild的右指向A,最后将原来指向A的指针指向grandchild。
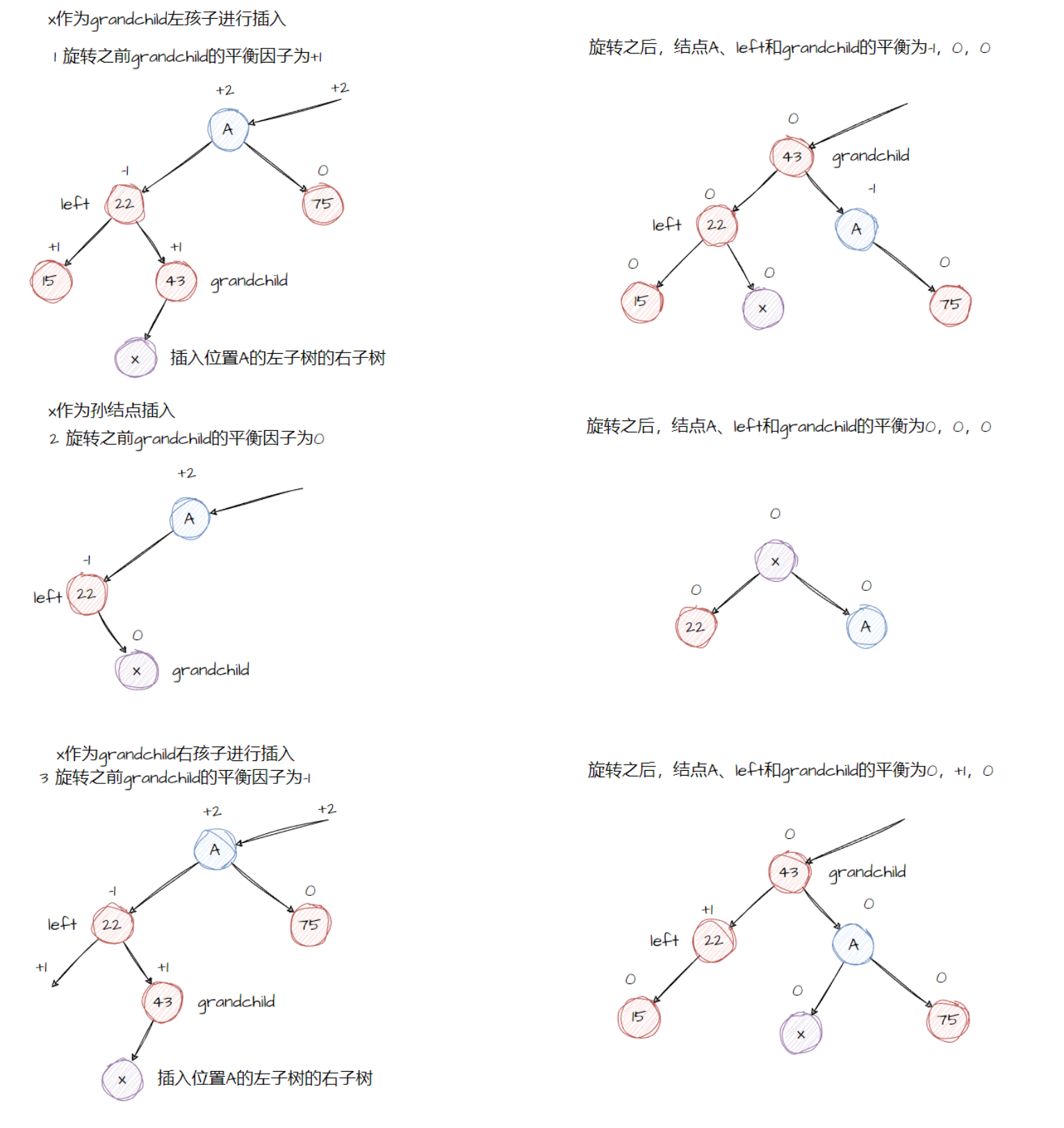
在执行LR旋转后,调整结点的平衡因子取决于旋转之前的grandchild结点的原平衡因子,所以代码中要对原本的grandchild的平衡因子进行判断。
- grandchild的平衡因子为+1,就将A的平衡因子为-1,将left结点的平衡因子设置为0
- grandchild的平衡因子为0,就将A的平衡因子为0,将left结点的平衡因子设置为0
- grandchild的平衡因子为-1,就将A的平衡因子为0,将left结点的平衡因子设置为+1
在所有的情况下,旋转后的grandchild的平衡因子都是0,其他的结点的平衡因子都不发生改变。
为了有直观的影响,我这里画出了LR旋转步骤过程
三种不用情况的平衡因子的更新情况分类
RR旋转
当x位于A的右子树的右子树上,执行RR旋转操作。RR旋转和LL旋转是对称的关系。设A的右子节点为right。要执行RR旋转,将A的右指针指向right的左子结点,right的左指针指向A,原来指向A的指针指向为right。完成操作后,将A和left的平衡因子都修改为0。其他结点的平衡因子都不发生改变。
RL旋转
执行RL旋转之后,调整结点的平衡因子取决旋转前的grandchild结点的原平衡因子,这里存在三种情况需要进行考虑。其他和LR旋转是对称的
- 如果grandchild结点的原平衡因子为+1,将A的平衡因子更新为0,right的平衡因子设置为-1
- 如果grandchild结点的原平衡因子为0,将A的平衡因子更新为0,right的平衡因子设置为0
- 如果grandchild结点的原平衡因子为-1,将A的平衡因子更新为+1,right的平衡因子设置为0
二叉搜索树的接口定义
bistree_init
函数原型:**void bistree_init(bistree_t* tree, int(*compare)(const void key1, const void key2), void(destroy)(void data))
返回值:无
函数说明:初始化函数由tree指定一颗二叉搜索树进行初始化。初始化必须在使用其他二叉搜索树前进行调用。函数指针compare指定一个由用户自定义的比较函数。这个比较函数在key1大于key2返回1,在key1小于key2返回0。destroy指定一种由用户自定义的释放动态内存空间的方法。如果二叉树的内存不需要进行释放,该值为NULL。
时间复杂度:O(1)
bistree_destory
函数原型:
返回值:无
函数说明:该函数用于销毁参数tree指定的二叉搜索树。在调用该函数对二叉搜索树进行销毁,之后任何对树的任何操作都不允许。除非用户重新初始化二叉搜索树,如果在初始二叉搜索树设置的形参
待续
实现代码
接口代码
#ifndef __BITREE_H__
#define __BITREE_H__
#include <stdio.h>
/*************************************************************
* 二叉树结点结构体
*************************************************************/
typedef struct __bitree_node
{
void *data;
struct __bitree_node *left;
struct __bitree_node *right;
}bitree_node_t;
/*************************************************************
* 二叉树结构体
*************************************************************/
typedef struct __bitree
{
int size;
int (*compare)(const void *key1, const void *key2);
void (*destroy)(void *data);
bitree_node_t *root;
}bitree_t;
/*************************************************************
* 二叉树函数接口
*************************************************************/
/* 二叉树初始化 */
void bitree_init(bitree_t* tree, void (*destroy)(void *data));
/* 二叉树析构 */
void bitree_destroy(bitree_t* tree);
/* 二叉树左插 */
int bitree_ins_left(bitree_t* tree, bitree_node_t* node, const void *data);
/* 二叉树右插 */
int bitree_ins_right(bitree_t* tree, bitree_node_t* node, const void *data);
/* 二叉树左结点去除 */
void bitree_rem_left(bitree_t* tree, bitree_node_t* node);
/* 二叉树右结点去除 */
void bitree_rem_right(bitree_t* tree, bitree_node_t* node);
/* 二叉树合并 */
int bitree_rem_merge(bitree_t* merge, bitree_t* left, bitree_t *right, const void *data);
/*************************************************************
* 宏定义
*************************************************************/
#define BITREE_SIZE(__tree) ((__tree)->size)
#define BITREE_ROOT(__tree) ((__tree)->root)
#define BITREE_IS_EOB(__node) ((__node) == NULL)
#define BITREE_IS_LEAF(__node) ((__node)->left == NULL) && ((__node)->right == NULL)
#define BITREE_DATA(__node) ((__node)->data)
#define BITREE_LEFT(__node) ((__node)->left)
#define BITREE_RIGHT(__node) ((__node)->right)
#endif /* bitree.h */
实现代码
#include "bistress.h"
#include <stdlib.h>
#include <string.h>
static void rotate_left(bitree_node_t **node);
static void rotate_right(bitree_node_t **node);
static void destory_left(bistree_t *tree, bitree_node_t *node);
static void destory_right(bistree_t *tree, bitree_node_t *node);
static int insert(bistree_t *tree, bitree_node_t **node, const void *data, int *balanced);
static int hide(bistree_t *tree, bitree_node_t *node, const void* data);
static void rotate_left(bitree_node_t **node)
{
bitree_node_t *left;
bitree_node_t *grandchild;
left = BITREE_LEFT(*node);
if(((avl_node_t*)BITREE_DATA(left))->factor == AVL_LFT_HEAVY)
{
BITREE_LEFT(*node) = BITREE_RIGHT(left);
BITREE_RIGHT(left) = *node;
((avl_node_t*)BITREE_DATA(*node))->factor = AVL_BALANCED;
((avl_node_t*)BITREE_DATA(left))->factor = AVL_BALANCED;
*node = left;
}
else
{
grandchild = BITREE_RIGHT(left);
BITREE_RIGHT(left) = BITREE_LEFT(grandchild);
BITREE_LEFT(*node) = BITREE_RIGHT(grandchild);
BITREE_RIGHT(grandchild) = *node;
switch (((avl_node_t*)BITREE_DATA(grandchild))->factor)
{
case AVL_LFT_HEAVY:
((avl_node_t*)BITREE_DATA(*node))->factor = AVL_RGT_HEAVY;
((avl_node_t*)BITREE_DATA(left))->factor = AVL_BALANCED;
break;
case AVL_BALANCED:
((avl_node_t*)BITREE_DATA(*node))->factor = AVL_BALANCED;
((avl_node_t*)BITREE_DATA(left))->factor = AVL_BALANCED;
case AVL_RGT_HEAVY:
((avl_node_t*)BITREE_DATA(*node))->factor = AVL_BALANCED;
((avl_node_t*)BITREE_DATA(left))->factor = AVL_LFT_HEAVY;
default:
break;
}
((avl_node_t*)BITREE_DATA(grandchild))->factor = AVL_BALANCED;
*node = grandchild;
}
return;
}
static void rotate_right(bitree_node_t **node)
{
bitree_node_t *right;
bitree_node_t *grandchild;
if(((avl_node_t*)BITREE_DATA(right))->factor == AVL_RGT_HEAVY)
{
BITREE_LEFT(*node) = BITREE_RIGHT(right);
BITREE_RIGHT(right) = *node;
((avl_node_t*)BITREE_DATA(*node))->factor = AVL_BALANCED;
((avl_node_t*)BITREE_DATA(right))->factor = AVL_BALANCED;
*node = right;
}
else
{
grandchild = BITREE_RIGHT(right);
BITREE_RIGHT(right) = BITREE_LEFT(grandchild);
BITREE_LEFT(*node) = BITREE_RIGHT(grandchild);
BITREE_RIGHT(grandchild) = *node;
switch (((avl_node_t*)BITREE_DATA(grandchild))->factor)
{
case AVL_LFT_HEAVY:
((avl_node_t*)BITREE_DATA(*node))->factor = AVL_BALANCED;
((avl_node_t*)BITREE_DATA(right))->factor = AVL_RGT_HEAVY;
break;
case AVL_BALANCED:
((avl_node_t*)BITREE_DATA(*node))->factor = AVL_BALANCED;
((avl_node_t*)BITREE_DATA(right))->factor = AVL_BALANCED;
case AVL_RGT_HEAVY:
((avl_node_t*)BITREE_DATA(*node))->factor = AVL_LFT_HEAVY;
((avl_node_t*)BITREE_DATA(right))->factor = AVL_BALANCED;
default:
break;
}
((avl_node_t*)BITREE_DATA(grandchild))->factor = AVL_BALANCED;
*node = grandchild;
}
return;
}
static void destory_left(bistree_t *tree, bitree_node_t *node)
{
bitree_node_t **position;
if(BISTREE_SIZE(tree) == 0)
{
return;
}
if(node == NULL)
{
position = &tree->root;
}
else
{
position = &node->left;
}
if(*position != NULL)
{
destory_left(tree, *position);
destory_right(tree, *position);
if(tree->destroy != NULL)
{
tree->destroy(((avl_node_t*)(*position)->data)->data);
}
/* 使用destroy函数对树的动态内存进行释放 */
free((*position)->data);
free(*position);
*position = NULL;
tree->size--;
}
return;
}
static void destory_right(bistree_t *tree, bitree_node_t *node)
{
bitree_node_t **position;
if(BISTREE_SIZE(tree) == 0)
{
return;
}
if(node == NULL)
{
position = &tree->root;
}
else
{
position = &node->right;
}
if(*position != NULL)
{
destory_left(tree, *position);
destory_right(tree, *position);
if(tree->destroy != NULL)
{
tree->destroy(((avl_node_t*)(*position)->data)->data);
}
/* 使用destroy函数对树的动态内存进行释放 */
free((*position)->data);
free(*position);
*position = NULL;
tree->size--;
}
return;
}
static int insert(bistree_t *tree, bitree_node_t **node, const void *data, int *balanced)
{
avl_node_t *avl_data;
int cmpval;
int retval;
/* 将数据插入到树中 */
if(BITREE_IS_EOB(*node))
{
if((avl_data = (avl_node_t*)malloc(sizeof(avl_node_t))) == NULL)
{
return -1;
}
avl_data->factor = AVL_BALANCED;
avl_data->hidden = 0;
avl_data->data = (void*)data;
return bitree_ins_left(tree, *node, avl_data);
}
else
{
cmpval = tree->compare(data, ((avl_node_t*)BITREE_DATA(*node))->data);
if(cmpval < 0)
{
if(BITREE_IS_EOB(BITREE_LEFT(*node)))
{
if((avl_data = (avl_node_t*)malloc(sizeof(avl_node_t))) == NULL)
{
return -1;
}
avl_data->factor = AVL_BALANCED;
avl_data->hidden = 0;
avl_data->data = (void*)data;
if(bitree_ins_left(tree, *node, avl_data) != 0)
{
return -1;
}
*balanced = 0;
}
else
{
if((retval = insert(tree, BITREE_LEFT(*node), data, balanced)) != 0)
{
return retval;
}
}
if(!(*balanced))
{
switch (((avl_node_t*)BITREE_DATA(*node))->factor)
{
case AVL_LFT_HEAVY:
rotate_left(node);
*balanced = 1;
break;
case AVL_BALANCED:
((avl_node_t*)BITREE_DATA(*node))->factor = AVL_LFT_HEAVY;
break;
case AVL_RGT_HEAVY:
((avl_node_t*)BITREE_DATA(*node))->factor = AVL_BALANCED;
*balanced = 1;
default:
break;
}
}
}
else if(cmpval > 0)
{
if(BITREE_IS_EOB(BITREE_LEFT(*node)))
{
if((avl_data = (avl_node_t*)malloc(sizeof(avl_node_t))) == NULL)
{
return -1;
}
avl_data->factor = AVL_BALANCED;
avl_data->hidden = 0;
avl_data->data = (void*)data;
if(bitree_ins_right(tree, *node, avl_data) != 0)
{
return -1;
}
*balanced = 0;
}
else
{
if((retval = insert(tree, BITREE_LEFT(*node), data, balanced)) != 0)
{
return retval;
}
}
if(!(*balanced))
{
switch (((avl_node_t*)BITREE_DATA(*node))->factor)
{
case AVL_LFT_HEAVY:
((avl_node_t*)BITREE_DATA(*node))->factor = AVL_BALANCED;
*balanced = 1;
break;
case AVL_BALANCED:
((avl_node_t*)BITREE_DATA(*node))->factor = AVL_RGT_HEAVY;
break;
case AVL_RGT_HEAVY:
rotate_right(node);
*balanced = 1;
default:
break;
}
}
}
else
{
if(!((avl_node_t*)BITREE_DATA(*node))->hidden)
{
return 1;
}
else
{
if(tree->destroy != NULL)
{
tree->destroy(((avl_node_t*)BITREE_DATA(*node))->data);
}
((avl_node_t*)BITREE_DATA(*node))->data = (void*)data;
((avl_node_t*)BITREE_DATA(*node))->hidden = 0;
*balanced = 1;
}
}
}
return 0;
}
static int hide(bistree_t *tree, bitree_node_t *node, const void* data)
{
int cmpval;
int retval;
if(BITREE_IS_EOB(node))
{
return -1;
}
cmpval = tree->compare(data, ((avl_node_t*)BITREE_DATA(node))->data);
if(cmpval < 0)
{
retval = hide(tree, BITREE_LEFT(node), data);
}
else if(cmpval > 0)
{
retval = hide(tree, BITREE_RIGHT(node), data);
}
else
{
((avl_node_t*)BITREE_DATA(node))->hidden = 1;
retval = 0;
}
return retval;
}
static int lookup(bistree_t* tree, bitree_node_t *node, void **data)
{
int cmpval;
int retval;
if(BITREE_IS_EOB(node))
{
return -1;
}
cmpval = tree->compare(data, ((avl_node_t*)BITREE_DATA(node))->data);
if(cmpval < 0)
{
retval = look_up(tree, BITREE_LEFT(node), data);
}
else if(cmpval > 0)
{
retval = look_up(tree, BITREE_RIGHT(node), data);
}
else
{
if(!((avl_node_t*)BITREE_DATA(node))->hidden)
{
*data = ((avl_node_t*)BITREE_DATA(node))->data;
retval = 0;
}
else
{
return -1;
}
}
return retval;
}
void bistree_init(bistree_t* tree, int(*compare)(const void *key1, const void *key2), void(*destroy)(void *data))
{
bitree_init(tree, destroy);
tree->compare = compare;
return;
}
void bistree_destroy(bistree_t* tree, const void *data)
{
destory_left(tree, NULL);
memset(tree, 0, sizeof(bistree_t));
return;
}
int bistree_insert(bistree_t* tree, const void *data)
{
int balanced = 0;
return insert(tree, &BITREE_ROOT(tree), data, &balanced);
}
int bistree_remove(bistree_t* tree, const void *data)
{
return hide(tree, BITREE_ROOT(tree), data);
}
int bistree_lookup(bistree_t* tree, void *data)
{
return lookup(tree, BITREE_ROOT(tree), data);
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· 写一个简单的SQL生成工具
· AI 智能体引爆开源社区「GitHub 热点速览」