laplacian matrix的几种形式

1. 一般laplacian矩阵（ordinary laplacian matrix）

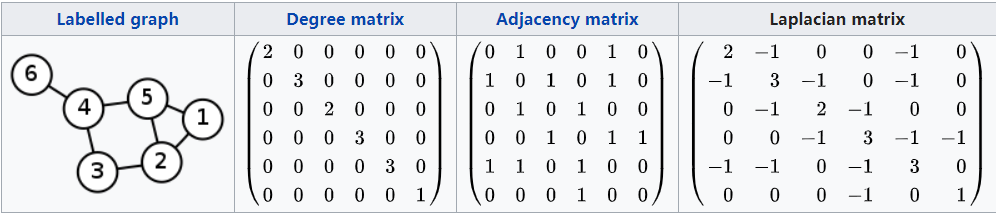
　　对于给定n个顶点的简单图G, 它的Laplacian matrix 定义如下

L = D - A

　　D是图G的度矩阵，A为图G的邻接矩阵。（例子来源：wikipedia）

 

2. laplacian matrix的几种常见的表示形式

　　其中deg(v_i)表示顶点v_i的度，L为普通laplacian matrix。

　　（1）对称规范化拉普拉斯矩阵-Symmetric normalized Laplacian

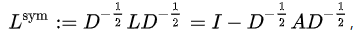
分析可得, L^{sym中的元素由下面公式给出：}

 

　　（2）RW规范化拉普拉斯矩阵-Random walk normalized Laplacian

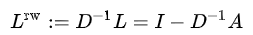
L^rw中的元素由下面公式给出：

 

 

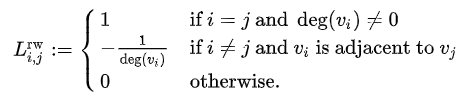
　　（3）广义拉普拉斯矩阵-Generalized Laplacian

Generalized Laplacian 矩阵中元素由下面公式给出

 

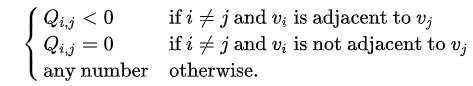
注意到，普通的laplacian matrix便属于Generalized Laplacian 

3. laplacian矩阵的性质

　　1. laplacian矩阵是对称，半正定矩阵。

　　2. 存在一个为0的特征值，即rank(L) = n - 1。

　　3. 行和，列和均等于0。

　　4. L的Raleigh商

R(L, x) = x^HLx / x^Hx

R(L, x)是x的连续函数，max(R)就是L的最大特征值, min(R)就是L的最小特征值。