【HDU 5382】 GCD?LCM! (数论、积性函数)
GCD?LCM!
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 316 Accepted Submission(s): 200
OutputT lines, find S(n) mod 258280327.Sample Input8 1 2 3 4 10 100 233 11037Sample Output1 5 13 26 289 296582 3928449 213582482AuthorSXYZSource
【分析】
这题好神啊。。。又涨姿势了。。
$$f(n)=\sum\sum [lcm(i,j)+gcd(i,j)>=n]$$
$$=\sum_{i'}\sum_{j'}\sum_{d}[d+i'*j'*d>=n]$$
$$=\sum_{i'}\sum_{j'}\sum_{d}[(i'*j'+1)*d>=n]$$
$$=\sum_{i'}\sum_{j'}\sum_{d}[(i'*j'+1)*d>=n-1]-\sum_{i'}\sum_{j'}\sum_{d}[(i'*j'+1)*d==n-1]$$
设$G(n)=\sum_{d|n}[gcd(d,\dfrac{n}{d})==1]$
则
$f(n)=f(n-1)-\sum_{d} G(\dfrac{n-1}{d}-1)+(2*n-1)$【后面加的是要注意i和j的范围!!!】
$G$G是积性函数,且$G(p^k)=2$
则可以$O(n)$筛出来。。
然后f前面的累加,后面的nlogn处理。
然后再累加即可。

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 #define Maxn 1000010 8 #define Mod 258280327 9 10 int pri[Maxn],pl,g[Maxn],t[Maxn],f[Maxn]; 11 bool vis[Maxn]; 12 13 void init() 14 { 15 memset(vis,0,sizeof(vis)); 16 pl=0;g[1]=1; 17 for(int i=2;i<=Maxn-10;i++) 18 { 19 if(!vis[i]) pri[++pl]=i,g[i]=2; 20 for(int j=1;j<=pl;j++) 21 { 22 if(pri[j]*i>Maxn-10) break; 23 vis[i*pri[j]]=1; 24 if(i%pri[j]==0) g[i*pri[j]]=g[i]; 25 else g[i*pri[j]]=2*g[i]%Mod; 26 if(i%pri[j]==0) break; 27 } 28 } 29 for(int i=1;i<=Maxn-10;i++) 30 { 31 for(int j=i;j<=Maxn-10;j+=i) 32 { 33 t[j]=(t[j]+g[j/i-1])%Mod; 34 } 35 } 36 for(int i=1;i<=Maxn-10;i++) f[i]=(f[i-1]+(2*i-1)-t[i-1])%Mod; 37 for(int i=1;i<=Maxn-10;i++) f[i]=((f[i]+f[i-1])%Mod+Mod)%Mod; 38 } 39 40 int main() 41 { 42 init(); 43 int T; 44 scanf("%d",&T); 45 while(T--) 46 { 47 int n; 48 scanf("%d",&n); 49 printf("%d\n",f[n]); 50 } 51 return 0; 52 }
【有一点点容斥的东东在么?】
2017-04-27 15:28:52
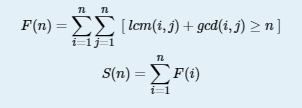


 浙公网安备 33010602011771号
浙公网安备 33010602011771号