【BZOJ 3235】 3235: [Ahoi2013]好方的蛇 （单调栈+容斥原理）

3235: [Ahoi2013]好方的蛇

Time Limit: 10 Sec  Memory Limit: 64 MB
Submit: 187  Solved: 95

Description

有一天，可爱的蛇心花怒放，把自己变成了一个正方形！但是她改变的时候
被induce了导致改变出了些问题....  

按照预设，她应该变成一个N*N的全黑正方形，但是这个正方形出现了一些白的格子...现在她的身体不幸出了些小反应，定义一个subsnake是一个至少有两格的全黑矩形。 

现在蛇想让你帮忙求一下一共有多少对不相交的subsnake，答案模10007。

Input

第一行一个整数 N,   接下来N行，每行一个长度为N的字符串，如果是B，那么是黑的，如果是 W那么是白的。

Output

一行一个整数，表示答案

Sample Input

3
BBW
BBW
BWW

Sample Output

5

HINT

N<=1000

Source

 

 

【分析】

　　首先考虑白点不能选。f[i][j]表示以(i,j)为左上角的矩形个数。发现这个东西其实类似有障碍点的最大子矩阵问题。【其实求和更容易一些，用一个单调栈就好了。方法自己Y吧。。

　　但是怎么统计两两不相交呢？

　　首先枚举(i,j)为左上角的矩形，右下角在其左方或上方的矩形就是不相交的。

　　但是，有可能算重复。就是这种情况：

　　

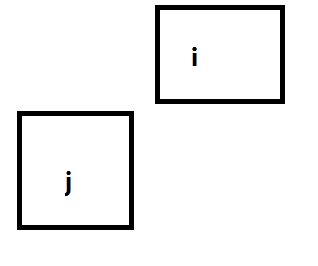
　　减掉就好了。

 

 1 #include<cstdio>
 2 #include<cstdlib>
 3 #include<cstring>
 4 #include<iostream>
 5 #include<algorithm>
 6 using namespace std;
 7 #define Maxn 1010
 8 #define LL long long
 9 #define Mod 10007
10 
11 char s[Maxn][Maxn];
12 int mx[Maxn][Maxn],sm[Maxn][Maxn][5];
13 int q[Maxn];
14 
15 int n;
16 void ffind(int k)
17 {
18     if(k&1)
19     {
20         for(int j=1;j<=n;j++)
21         {
22             int l=1,r=0;q[0]=0;
23             for(int i=1;i<=n;i++)
24             {
25                 if(mx[i][j]==0) {sm[i][j][k]=0;q[r]=i;l=r+1;continue;}
26                 while(l<=r&&mx[i][j]<=mx[q[r]][j]) r--;
27                 sm[i][j][k]=sm[q[r]][j][k]+(i-q[r])*mx[i][j];
28                 q[++r]=i;
29             }
30         }
31     }
32     else
33     {
34         for(int j=1;j<=n;j++)
35         {
36             int l=1,r=0;q[0]=n+1;
37             for(int i=n;i>=1;i--)
38             {
39                 if(mx[i][j]==0) {sm[i][j][k]=0;q[r]=i;l=r+1;continue;}
40                 while(l<=r&&mx[i][j]<=mx[q[r]][j]) r--;
41                 sm[i][j][k]=sm[q[r]][j][k]+(q[r]-i)*mx[i][j];
42                 q[++r]=i;
43             }
44         }
45     }
46     
47     for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(sm[i][j][k]) sm[i][j][k]--;
48     if(k==2) for(int i=n;i>=1;i--) for(int j=1;j<=n;j++)
49       sm[i][j][k]=(sm[i][j-1][k]+sm[i+1][j][k]-sm[i+1][j-1][k]+sm[i][j][k])%Mod;
50     else if(k==3) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
51       sm[i][j][k]=(sm[i][j-1][k]+sm[i-1][j][k]-sm[i-1][j-1][k]+sm[i][j][k])%Mod;
52         
53 }
54 
55 int main()
56 {
57     scanf("%d",&n);
58     for(int i=1;i<=n;i++) scanf("%s",s[i]+1);
59     
60     memset(mx,0,sizeof(mx));
61     for(int i=1;i<=n;i++) for(int j=n;j>=1;j--) mx[i][j]=(s[i][j]=='W')?0:mx[i][j]=1+mx[i][j+1];
62     ffind(0);//zuo shang
63     ffind(1);//zuo xia
64     for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) mx[i][j]=(s[i][j]=='W')?0:mx[i][j]=1+mx[i][j-1];
65     ffind(2);//you shang
66     ffind(3);//you xia
67     
68     
69     int ans=0;
70     for(int i=1;i<=n;i++)
71      for(int j=1;j<=n;j++)
72      {
73          ans+=1LL*sm[i][j][0]*(sm[n][j-1][3]+sm[i-1][n][3]-sm[i-1][j-1][3])%Mod;
74          ans-=1LL*sm[i][j][1]*sm[i+1][j-1][2]%Mod;
75          ans%=Mod;
76      }
77     ans=(ans+Mod)%Mod;
78     printf("%d\n",ans);
79     return 0;
80 }
View Code

 

2017-04-20 10:52:07

　　

posted @ 2017-04-20 10:52  konjak魔芋  阅读(239)  评论(0)  编辑  收藏  举报