【BZOJ 3218】 3218: a + b Problem（最小割+可持久化线段树）

 

 

3218: a + b Problem

Time Limit: 20 Sec  Memory Limit: 40 MB
Submit: 1440  Solved: 545

Description

Input

Output

Sample Input

Sample Output

HINT

Source

 

 

【分析】

　　这题建图很神哦！

　　其实只是边的合并。

　　就是说，原本海陆型建图就好了的。

　　

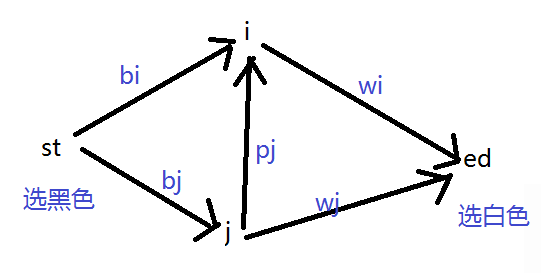
　　但是这样有一点问题，就是pj只算一次的，但是这样跑算了很多次。

　　改一改图。

　　

　　这样就好了。

　　但是边很多。

　　一开始没注意那个l~r的，就觉得嗯，开一些辅助点合并一下边。

　　后来发现还有l~r的限制，其实也是开一些辅助点合并一下边，但是这里就有点高级了。

　　就是值考虑l<=a<=r的话就是开个权值线段树然后用线段树上的点作为辅助点。

　　但是还有一个条件是i<=j的时候才算，所以是可持久化线段树。

　　关于辅助点，其实上面的j‘就是辅助点，照着做就好了。

 

  1 #include<cstdio>
  2 #include<cstdlib>
  3 #include<cstring>
  4 #include<iostream>
  5 #include<algorithm>
  6 #include<queue>
  7 using namespace std;
  8 #define Maxn 5010
  9 #define Maxm 1000000000
 10 // #define Maxm 10
 11 #define INF 0x7fffffff
 12 // #define LL long long
 13 
 14 int mymin(int x,int y) {return x<y?x:y;}
 15 
 16 struct node
 17 {
 18     int x,y,f,o,next;
 19 }t[Maxn*210];
 20 int len,first[Maxn*40];
 21 
 22 void ins(int x,int y,int f)
 23 {
 24     if(y==0) return;
 25     t[++len].x=x;t[len].y=y;t[len].f=f;
 26     t[len].next=first[x];first[x]=len;t[len].o=len+1;
 27     t[++len].x=y;t[len].y=x;t[len].f=0;
 28     t[len].next=first[y];first[y]=len;t[len].o=len-1;
 29 }
 30 
 31 int dis[Maxn*40],st,ed;
 32 queue<int > q;
 33 bool bfs()
 34 {
 35     memset(dis,-1,sizeof(dis));
 36     while(!q.empty()) q.pop();
 37     dis[st]=0;q.push(st);
 38     while(!q.empty())
 39     {
 40         int x=q.front();
 41         for(int i=first[x];i;i=t[i].next) if(t[i].f>0)
 42         {
 43             int y=t[i].y;
 44             if(dis[y]==-1)
 45             {
 46                 dis[y]=dis[x]+1;
 47                 q.push(y);
 48             }
 49         }
 50         q.pop();
 51     }
 52     if(dis[ed]==-1) return 0;
 53     return 1;
 54 }
 55 
 56 int ffind(int x,int flow)
 57 {
 58     if(x==ed) return flow;
 59     int now=0;
 60     for(int i=first[x];i;i=t[i].next) if(t[i].f>0)
 61     {
 62         int y=t[i].y;
 63         if(dis[y]==dis[x]+1)
 64         {
 65             int a=ffind(y,mymin(flow-now,t[i].f));
 66             t[i].f-=a;
 67             t[t[i].o].f+=a;
 68             now+=a;
 69         }
 70         if(now==flow) break;
 71     }
 72     if(now==0) dis[x]=-1;
 73     return now;
 74 }
 75 
 76 int ans=0;
 77 void max_flow()
 78 {
 79     while(bfs())
 80     {
 81         ans-=ffind(st,INF);
 82     }
 83 }
 84 void output()
 85 {
 86     for(int i=1;i<=len;i+=2)
 87     {
 88         printf("%d -> %d %d\n",t[i].x,t[i].y,t[i].f);
 89     }printf("\n");
 90 }
 91 
 92 int rt[Maxn],cnt;
 93 struct nnode
 94 {
 95     int lc,rc;
 96 }tr[Maxn*40];
 97 
 98 
 99 void add(int l,int r,int x,int y,int a,int id)
100 {
101     ins(y,x,INF);
102     ins(y,id,INF);
103     if(l==r) return;
104     int mid=(l+r)>>1;
105     if(a<=mid)
106     {
107         tr[y].lc=++cnt;tr[y].rc=tr[x].rc;
108         add(l,mid,tr[x].lc,tr[y].lc,a,id);
109     }
110     else
111     {
112         tr[y].rc=++cnt;tr[y].lc=tr[x].lc;
113         add(mid+1,r,tr[x].rc,tr[y].rc,a,id);
114     }
115 }
116 
117 void add2(int l,int r,int x,int al,int ar,int id)
118 {
119     if(l==al&&r==ar)
120     {
121         ins(id,x,INF);
122         return;
123     }
124     int mid=(l+r)>>1;
125     if(ar<=mid) add2(l,mid,tr[x].lc,al,ar,id);
126     else if(al>mid) add2(mid+1,r,tr[x].rc,al,ar,id);
127     else
128     {
129         add2(l,mid,tr[x].lc,al,mid,id);
130         add2(mid+1,r,tr[x].rc,mid+1,ar,id);
131     }
132 }
133 
134 
135 int main()
136 {
137     int n;
138     scanf("%d",&n);
139     st=n*2+1,ed=st+1;cnt=ed;
140     rt[0]=0;
141     len=0;
142     memset(first,0,sizeof(first));
143     for(int i=1;i<=n;i++)
144     {
145         int a,b,c,w,al,ar,p;
146         scanf("%d%d%d%d%d%d",&a,&b,&w,&al,&ar,&p);
147         ans+=b+w;
148         ins(st,i,b);ins(i,ed,w);
149         ins(i,i+n,p);
150         rt[i]=++cnt;
151         add(0,Maxm,rt[i-1],rt[i],a,i);
152         add2(0,Maxm,rt[i],al,ar,i+n);
153     }
154     // output();
155     max_flow();
156     printf("%d\n",ans);
157     return 0;
158 }
View Code

 

2017-04-06 22:05:14

 

posted @ 2017-04-06 22:05  konjak魔芋  阅读(563)  评论(0)  编辑  收藏  举报