-【网络流总结】

最大流就不说了。。Dinic。。。

发个模板：

  1 #include<cstdio>
  2 #include<cstdlib>
  3 #include<cstring>
  4 #include<iostream>
  5 #include<algorithm>
  6 #include<queue>
  7 using namespace std;
  8 #define Maxn 210
  9 #define Maxm 10010
 10 #define INF 0xfffffff
 11 
 12 int fa[Maxn],first[Maxn],dis[Maxn];
 13 bool map[Maxn][Maxn];
 14 
 15 struct node
 16 {
 17     int x,y,f,o,next;
 18 };
 19 node t[10*Maxm],tt[10*Maxm];int len;
 20 
 21 int st,ed;
 22 int n,m,k;
 23 
 24 int mymin(int x,int y) {return x<y?x:y;}
 25 
 26 void ins(int x,int y,int f)
 27 {
 28     tt[++len].x=x;tt[len].y=y;tt[len].f=f;
 29     tt[len].next=first[x];first[x]=len;tt[len].o=len+1;
 30     tt[++len].x=y;tt[len].y=x;tt[len].f=0;
 31     tt[len].next=first[y];first[y]=len;tt[len].o=len-1;
 32 }
 33 
 34 int ffind(int x)
 35 {
 36     if(fa[x]!=x) fa[x]=ffind(fa[x]);
 37     return fa[x];
 38 }
 39 
 40 queue<int > q;
 41 bool bfs()
 42 {
 43     while(!q.empty()) q.pop();
 44     memset(dis,-1,sizeof(dis));
 45     q.push(st);dis[st]=0;
 46     while(!q.empty())
 47     {
 48         int x=q.front();q.pop();
 49         for(int i=first[x];i;i=t[i].next) if(t[i].f>0)
 50         {
 51             int y=t[i].y;
 52             if(dis[y]==-1)
 53             {
 54                 dis[y]=dis[x]+1;
 55                 q.push(y);
 56             }
 57         }
 58     }
 59     if(dis[ed]==-1) return 0;
 60     return 1;
 61 }
 62 
 63 int find_flow(int x,int flow)
 64 {
 65     if(x==ed) return flow;
 66     int now=0;
 67     for(int i=first[x];i;i=t[i].next) if(t[i].f>0)
 68     {
 69         int y=t[i].y;
 70         if(dis[y]==dis[x]+1)
 71         {
 72             int a=find_flow(y,mymin(t[i].f,flow-now));
 73             t[i].f-=a;
 74             t[t[i].o].f+=a;
 75             now+=a;
 76                 if(now==flow) break;
 77         }
 78     }
 79     if(now==0) dis[x]=-1;
 80     return now;
 81 }
 82 
 83 int max_flow()
 84 {
 85     int ans=0;
 86     while(bfs()) 
 87         ans+=find_flow(st,INF);
 88     return ans;
 89 }
 90 
 91 bool check(int x)
 92 {
 93     for(int i=1;i<=len;i++) t[i]=tt[i];
 94     for(int i=len-4*n+1;i<=len;i+=2) t[i].f=x;
 95     return max_flow()==n*x;
 96 }
 97 
 98 void finda()
 99 {
100     int l=0,r=n*n;
101     while(l<r)
102     {
103         int mid=(l+r+1)>>1;
104         if(check(mid)) l=mid;
105         else r=mid-1;
106     }
107     printf("%d\n",l);
108 }
109 
110 int main()
111 {
112     int T;
113     scanf("%d",&T);
114     while(T--)
115     {
116         len=0;
117         memset(first,0,sizeof(first));
118         memset(map,0,sizeof(map));
119         scanf("%d%d%d",&n,&m,&k);
120         for(int i=1;i<=m;i++)
121         {
122             int x,y;
123             scanf("%d%d",&x,&y);
124             map[x][y]=1;
125         }
126         for(int i=1;i<=n;i++) fa[i]=i;
127         for(int i=1;i<=k;i++)
128         {
129             int x,y;
130             scanf("%d%d",&x,&y);
131             fa[ffind(x)]=ffind(y);
132         }
133         for(int i=1;i<=n;i++)
134          for(int j=1;j<=n;j++) if(ffind(i)==ffind(j))
135          {
136              for(int k=1;k<=n;k++) if(map[j][k])
137               map[i][k]=1;
138          }
139         for(int i=1;i<=n;i++)
140          for(int j=1;j<=n;j++) if(map[i][j])
141             ins(i,j+n,1);
142         st=2*n+1;ed=st+1;
143         for(int i=1;i<=n;i++) ins(st,i,INF);
144         for(int i=1;i<=n;i++) ins(i+n,ed,INF);
145         finda();
146     }
147     return 0;
148 }
149 
150 [HDU3081]

HDU 3081

主要步骤是：1、bfs求dis

　　　　　　2、find->尽量把流量流完

　　　　　　3、max——flow->每次bfs后find找尽增广路

费用流（是在流量最大的情况下费用最优）

跟最大流有点不一样，就是bfs那部分变成了加权的spfa。

模板：

运输问题

  1 #include<cstdio>
  2 #include<cstdlib>
  3 #include<cstring>
  4 #include<iostream>
  5 #include<algorithm>
  6 #include<queue>
  7 #include<cmath>
  8 using namespace std;
  9 #define Maxn 1010
 10 #define INF 0xfffffff
 11 
 12 struct node
 13 {
 14     int x,y,f,o,c,next;
 15 }t[Maxn*Maxn],tt[Maxn*Maxn];int len;
 16 int first[Maxn];
 17 
 18 int mymin(int x,int y) {return x<y?x:y;}
 19 int mymax(int x,int y) {return x>y?x:y;}
 20 
 21 void ins(int x,int y,int f,int c)
 22 {
 23     t[++len].x=x;t[len].y=y;t[len].f=f;t[len].c=c;
 24     t[len].next=first[x];first[x]=len;t[len].o=len+1;
 25     t[++len].x=y;t[len].y=x;t[len].f=0;t[len].c=-c;
 26     t[len].next=first[y];first[y]=len;t[len].o=len-1;
 27 }
 28 
 29 int st,ed;
 30 queue<int > q;
 31 int dis[Maxn],pre[Maxn],flow[Maxn];
 32 bool inq[Maxn];
 33 bool bfs()
 34 {
 35     while(!q.empty()) q.pop();
 36     memset(dis,63,sizeof(dis));
 37     memset(inq,0,sizeof(inq));
 38     q.push(st);dis[st]=0;flow[st]=INF;inq[st]=1;
 39     while(!q.empty())
 40     {
 41         int x=q.front();
 42         for(int i=first[x];i;i=t[i].next) if(t[i].f>0)
 43         {
 44             int y=t[i].y;
 45             if(dis[y]>dis[x]+t[i].c)
 46             {
 47                 dis[y]=dis[x]+t[i].c;
 48                 pre[y]=i;
 49                 flow[y]=mymin(flow[x],t[i].f);
 50                 if(!inq[y])
 51                 {
 52                     inq[y]=1;
 53                     q.push(y);
 54                 }
 55             }
 56         }
 57         inq[x]=0;q.pop();
 58     }
 59     if(dis[ed]>=INF-100000) return 0;
 60     return 1;
 61 }
 62 
 63 void output()
 64 {
 65     for(int i=1;i<=len;i+=2)
 66      printf("%d->%d %d %d\n",t[i].x,t[i].y,t[i].f,t[i].c);
 67     printf("\n");
 68 }
 69 
 70 int max_flow()
 71 {
 72     int ans=0,sum=0;
 73     while(bfs())
 74     {
 75         sum+=dis[ed]*flow[ed];
 76         ans+=flow[ed];
 77         int now=ed;
 78         while(now!=st)
 79         {
 80             t[pre[now]].f-=flow[ed];
 81             t[t[pre[now]].o].f+=flow[ed];
 82             now=t[pre[now]].x;
 83         }
 84     }
 85     return sum;
 86 }
 87 
 88 int m,n;
 89 
 90 void init()
 91 {
 92     scanf("%d%d",&m,&n);
 93     st=m+n+1;ed=st+1;
 94     len=0;
 95     memset(first,0,sizeof(first));
 96     for(int i=1;i<=m;i++)
 97     {
 98         int x;
 99         scanf("%d",&x);
100         ins(st,i,x,0);
101     }
102     for(int i=1;i<=n;i++)
103     {
104         int x;
105         scanf("%d",&x);
106         ins(i+m,ed,x,0);
107     }
108     for(int i=1;i<=m;i++)
109      for(int j=1;j<=n;j++)
110      {
111          int x;
112          scanf("%d",&x);
113          ins(i,j+m,INF,x);
114      }
115 }
116 
117 int main()
118 {
119     init();
120     for(int i=1;i<=len;i++) tt[i]=t[i];
121     int ans;
122     ans=max_flow();
123     printf("%d\n",ans);
124     for(int i=1;i<=len;i++) t[i]=tt[i];
125     for(int i=1;i<=len;i++) t[i].c=-t[i].c;
126     ans=max_flow();
127     printf("%d\n",-ans);
128     return 0;
129 }

No. 17 运输问题

上下界循环流（原图无源点汇点）

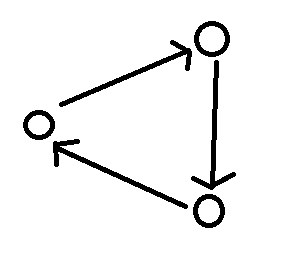
增加超级源点st，超级汇点ed。

对于一条边$x->y （k1<=f<=k2）$

拆边：

　　这时要判断满流。【只求了循环流可行解】

有费用

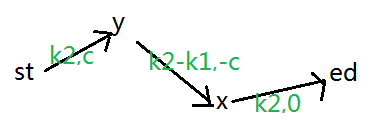
　　要判断满流

上下界网络流（原图有源点汇点）

只需加一条边变成循环流

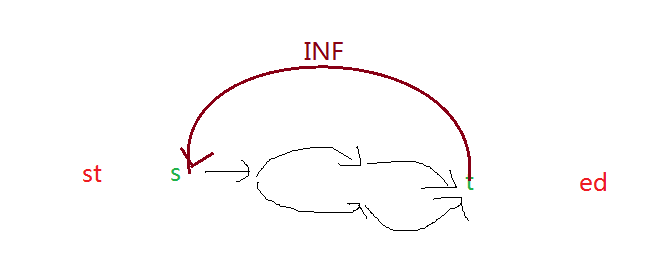
1、求最大流：删掉st与ed的边，从s到t在残图跑一遍最大流。

2、有费用：跑最大费用流

最大流的应用（标No的是网络流24题）

1、二分图匹配，可用最大流做。

【No.1飞行员问题】二分图匹配

【No.5圆桌问题】二分图多重匹配

【No.7试题库问题】二分图多重匹配

【HDU 3472 混合图的欧拉回路】

　　给你一个同时存在有向边以及无向边的混合图，你需要将所有的无向边定向，使得最后的有向图存在欧拉回路。欧拉回路的定义：所有点的入度=出度。

　　建模：首先随便给无向边定向。然后给所有点计算入度以及出度。如果此时有一个点的入度与出度的差是奇数，则一定不存在解。

　　不用考虑本来的有向边了，按照定向的无向边建图。你会知道某个点要修改多少条边的方向才能成立，于是是一个二分图的多重匹配问题。

2、公平分配问题（m个任务分给n个处理器，每个任务只有两种选择，求任务最多的处理器任务最少）

【LA 2531】

　　二分+最大流判满流

3、区间k覆盖问题（数轴上有一些带权的左闭右开区间，选出权值和最大的区间，使得任意一个数最多被k个区间覆盖）

　　对区间[u,v)加边u->v(1,w)，对相邻两点i->i+1 (k,0),可离散化。

·变形

【LA2796】你有2个房间，有365天，有n个人找你租房，第i个人要从第xi到第yi天要一个房(任意一个),付wi的钱，求怎样安排收的钱最多

1~365天建一个点，st连1流量为2费用为0。

　　根据输入的继续连边，比如第i个人要从第xi到第yi天要一个房(任意一个),付wi的钱那么建一条xi->yi+1流量为1，费用为wi的边。

　　最后求最大费用最大流（去负跑最小费用最大流即可）。

4、最多不相交路径（给一个有向图，求起点到终点最多几条不相交路径）

　　【No.最长不减子序列问题】

　　拆点，点容为1。（拆点方法也很常用啊）

5、最小路径覆盖

　　【No.4魔术球问题】

　　先每个点作为一条路径，但是每个点其实可以连一条入边一条出边，于是拆点，变成二分图最大匹配。

6、K取方格数问题。POJ 3422Kaka's Matrix Travels

题目大意：给定一个N*M的矩阵。每次游戏可以选择一条以矩阵左上角为起点，右下角为终点的路径，取走在这条路径上的所有方格内的权值。现在你有K次机会进行游戏，问最多能得到多少的权值。其中每个点可以被重复经过，但每个点上的权值最多只能被取走一次。

建模：每个点拆成两个点i、i'，建边i->i',容量为1，费用为-w，同时再建边i->i'，容量为无穷大，费用为0，表示每个点上的权值最多只能被取走一次且每个点能被经过多次。每个点u向它右边的点v建边u'->v，容量为无穷大，费用为0。向下同理。最后建立超级源汇S、T，S向矩阵左上角的点建边，容量为K，费用为0，矩阵右下角的点向汇点建边，容量为K，费用为0。最后跑一遍S到T的最小费用最大流，费用的相反数即答案。

7、K路径覆盖问题。【HDU】4862 Jump

给定一个N*M的矩阵，矩阵每个格子中有一个值（0~9），一开始你有活力值为0，然后你可以进行最多K次游戏，每次可以任选矩阵中的一个点作为顶点，然后开始游戏，每次你可以选择从这个点跳到它的右边的点或者下边的点或者不动。每次跳跃，你将支付两个点的曼哈顿距离-1的活力值，能量值可以为负。如果一次跳跃的起点和终点的格子中的值相同，你的活力值可以增加这个值大小的值。每个格子最多只可以经过一次且必须经过一次。每次游戏你可以跳任意多次，但不能违反规则。问最后能得到多少的活力值，如果不能遍历完所有点则输出-1。

建模：建立超级源汇S、T，S向所有格子建边，容量为1，费用为0，所有格子拆成两个，分别为i，i'，i到i'之间建边，容量为1，费用为比所有点的权和还小即可（可设为-1e5），保证优先遍历所有点。然后所有点向其右边的点j建边（i'，j，1，k-1-a），其中k-1为跳跃长度为k的花费，当一次跳跃的起点以及终点权值相同时，a等于该权值，否则，a等于0。所有点向其下方的点建边同上。最后建立超超级源汇S'，T'，S'向S建边，容量为K，费用为零，T向T'建边，容量为K，费用为0。最后跑最小费用流，如果cost的相反数/100000等于遍历的N*M（即遍历的所有点），则答案即（-cost）%100000，否则输出-1。

这里需要注意的是，由于最大流的是否并不一定是最小费用，所以在增广到增广路权和为正时即可退出费用流算法。

最小割的应用（最小割模型好多啊。。找找规律）

1、二分图最大独立集，可用最小割做。

【No.9方格取数问题】二分图最大权独立集

给定一个矩阵，矩阵内每个方格有一个权值，现在需要你取出一些边不相邻的方格内的权值，使得权值和最大。

建模：经典的最小割模型。最小割是最大流的对偶问题，最小割的容量等于最大流的容量。

建立超级源汇S，T。将图进行黑白染色，S和黑色的方格建边，容量为黑色方格权值，白色方格和T建边，容量为白色方格权值，黑色方格向相邻的白色方格建边，容量为无穷大。最后跑一遍最大流，所有点的权值和减去最大流的流量即答案。

·变形：

给定一个矩阵，矩阵内每个方格有一个权值，现在你可以取出一些方格的权值，如果取走了两个相邻的方格内的权值，则需要付出一些代价，你需要使得权值和 - 代价的值最大。

只要把中间的INF变成代价即可。

·变形2：

给定一个矩阵，矩阵内的方格内有两种属性（假设第一种属性为黑色，第二种为白色），的权值，每个方格可以取走其中一个属性的权值，可以取相邻的数，如果取走的相邻方格属于同一属性，需要花费相应的代价，问怎样取使得权值和-代价的值最大。

建模：现在我们依旧将图黑白染色，方格内属性和染色相同颜色的和源点建边，边权为该属性的权值；方格内属性和染色不同颜色的和汇点建边，边权为该属性的权值。同一方格内的两种属性之间建边，容量为无穷大，表示只能取其中一种属性，相邻方格颜色相同的建边，容量为相应的代价（这里所有边的方向均从源点指向汇点）。最后跑一遍最大流，所有点权值和减去最大流的流量即答案。

【No.24骑士共存问题】二分图最大点独立集

在一个 n*n 个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格（1-2矩形）。棋盘某些方格设置了障碍，骑士不得进入。对于给定的 n*n 个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击。

2、最大权闭合子图

【No.2太空飞行计划问题】

给定带全图G（权值可正可负），求一个权和最大的点集，使得起点在该点集中的任意弧，终点也在该点集中。

假设全部正值都选，负值都不选。

st->正值点，边权为点值，负值点->ed 边权为点值的相反数。若原图有边，则点点相连，权值为INF,跑最小割。

（简单割：只割源点汇点的可行割，这个模型的最小割是简单割哦）

3、最大密度子图。

给出一个无向图，找到一个点集，使得起点在该点集中的任意弧，终点也在该点集中，且使得这些点之间的边数除以点数的值（称为子图的密度）最大。

这个我只会一种没那么强但是好理解的方法。

建模一：01分数规划

E/V>=g => E-g*V>=0

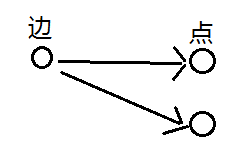转化为最大权闭合子图。

建模二：现在不会了。。。

4、项目分配问题

先来看一个函数。

项目分配问题便和这个函数息息相关的，因为用网络流可以求解这个函数的最小值。

建模：建立超级源汇S、T。S向所有的Xi建边，容量为ai，表示如果Xi取1则有ai的代价；所有的Xi向T建边，容量为bi，表示如果Xi取0则有bi的代价；然后存在（i,j）关系的Xi向Xj建边，容量为Cij，表示如果Xi取1，Xj取0时有Cij的代价。

最后跑一遍最小割，割的容量即该函数的最小值，也即取值的代价最小。

因为这样建模后，Xi要么取1，要么取0，又由于最小割的局部最大流全局最小割的特性，求出的最大流即最小割，割掉的边即Xi的取值，如果割掉了S和Xi之间的边，则说明Xi取1，否则Xi取0。这里我们又用到了网络流的特性：用流量的流向确定一些变量的取值。

让我们来看几道例题。

例一、【POJ】3469 Dual Core CPU

该题就是这个函数的基本原型。直接套用即可。

例二、【ZOJ】2539 Energy Minimization

本题稍作改变，只是将代价变成了绝对值而已，仍旧可以轻松解决。

例三、【HDU】4307 Matrix

本题略显复杂，一开始我们能得到一个显而易见的函数：

然后我们将这个式子进行一步步的分解，使其接近我们能求解的函数：

得到函数一个这样的形式以后，很惊讶的可以发现，等式右端括号里的部分和之前的f函数的定义惊人的相似！

当ai取1的时候，需要割掉代价为sum{bij}(1 <= j <= N)的S->Xi边，当ai取0的时候需要割掉代价为ci的Xi->T边，当ai取1且aj取0时需要割掉代价为bij的i->j边。

这个我们跑一遍最小割即括号中函数的最小值，用bij的总价值减去最小割的值即最大的D。

·变形【BZOJ 3996】

　化一下式子得到D=∑∑Ai∗Aj∗Bij−∑Ai∗Ci （Ai=0或1）
　　跟前面有一点点不同，想不到就多加一些点了。
　　S→Dot(i,j),流量为bij
　　Dot(i,j)→i 以及 Dot(i,j)→j,流量为 ∞
　　连边 i→T,流量为ci
设最小割为xx,那么答案就是 ∑∑Bij−x

　　但其实跟上面一样建图就好，你把所有情况对应的费用想好就能建图了。

　　就是st->i(ci) i->ed(Eij+Eji) i->j(Eij+Eji) j->ed(0) j->i(0)

　　把边合并，0边当然不用建，就应该比上面那种建发快很多了。

5、行列模型

【HDU】4975 A simple Gaussian elimination problem.

题目大意：告诉你每一行的元素和，每一列的元素和，每个元素的取值范围。如果无解输出“So naive!”。如果多解输出“So young!”。如果有唯一解，输出“So simple!”。

建模：首先每行i用一个结点ri表示，每列j用一个结点cj表示，建立超级源汇，源点向ri建边，容量为行i的元素和。cj向汇点建边，容量为列j的元素和。所有行向所有列建边，容量为取值上限。如果流量等于所有元素的和并且所有行的元素和等于所有列的元素和，则存在解，否则无解。然后需要判断是否多解。因为一个子四边形的四个角上的元素满足一个对角线上的元素都可以减小并且另一对角线上的元素都可以增大则存在多解。

判断是否多解这里有两种方法。

方法一：先扫描一下所有的边，（i,j）的反悔边容量即矩阵内[i][j]的容量假设扫描到了第r行，以vis[i][j]标记r行之前的位置i元素是否可以减小以及位置j元素是否可以增大，如果存在则vis[i][j]=1，否则vis[i][j]=0，现在看第r行的位置i以及位置j，如果位置i元素可以增大，则说明存在多解。否则等判断完r行的[i][j]以及[j][i]后更新vis[i][j]以及vis[j][i]。如果到最后都没有符合条件的子四边形存在则说明有唯一解。这里我们可以加一个优化，判断的时候如果该行（列）元素全部为0或者全部为最大值则可以跳过，因为即使存在也不会在这一行（列）内选择，该行（列）内是找不到需要的解的。

方法二：可以想到，如果选择一条边递归，然后从递归里出来了，说明没找到环，那么走这条边肯定找不到环，以后也不用走了，可以把这条边删了。或者这条边流量为0，也可以删了。

这样的话每条边最多只进一次，O(m)。参见http://www.cnblogs.com/yuiffy/p/3929369.html

6、最小割的关键割边。【ZOJ】2532 Internship

首先要明确关键割边的含义：增加这条边的容量则网络的流量即会增加。

建模：首先按照题目要求跑一遍最小割（最大流）。然后在残余网络上进行dfs（即只走有流量的边），先从源点开始进行dfs，将能到达的所有点都标记为1，然后从汇点开始再进行一次dfs，将能到达的点都标记为2。最后判断所有原图中的边（只看正向边），如果该条边的弧头被标记为1，弧尾被标记为2，则说明这条边即关键割边。

7、用INF边在最小割模型中限制选择

【BZOJ3144】三维的图，每个x,y选一个高度，每个高度有一个值v[x][y][h],相邻的(x,y)选的h的差要小于等于D，使得总的v最小，问最小值。

每个格子拆出40个点。连同S与T用40种代价串起来。即 p(x,y,z)->p(x,y,z+1)边权f(x,y,z+1)。然后 p(x,y,z)->p(x’,y’,z-d)边权inf (x,y)与(x’,y’)相邻

【BZOJ4663】

一张关系网，每一个人是这张关系网上的一个节点(节点编号为[0,n-1])，(一条 u->v 的边意味着信息可以从u 传递到 v)。0 号节点是信息的发出者，n-1 号节点是信息的接受者。
一个点可以经过多次，一条边也可以经过多次。一次成功的入侵要满足以下条件：对于任意一种可能的传递信息的方式(对应着一条从 0 到 n-1 的路径)，必须经过恰好一次被hack 的边。一次入侵的代价就是你选择 hack 掉的边的代价和。小叶子想要知道，如果你拥有 n+e 这样超神的智商，而你又想最小化代价，那么你入侵的代价会是多少呢？

解法：把反向边弄成INF，源点不能到的点删掉，就能保证同一条路径不会割两条边了。

8、海陆模型

http://www.cnblogs.com/Konjakmoyu/p/5502241.html

·类似

·类似2：

按点的属性建分属性图。LA 5905 Pool construction

题目大意：给定一个N * M的网格型地图，其中有的地方是坑，有的地方是草地，将草地变成坑需要花费D，将坑变为草地需要花费F，将坑的边界包围起来需要每单位花费B（因为以后要将坑灌水变成水池，为了防止水溢出，需要围起来）。其中坑可以不连续的分布，但是地图的最外围必须是草地（也就是说只能把坑补上）。问要将所有的坑的边界围起来需要花费的最小值是多少。

建模：每个点有两个属性，坑、或者是草。

最外围的坑必须是草，这个我们预处理解决掉。

然后我们建立超级源汇S、T。

S向草建边，容量为D，表示如果割掉S和草的联系，将这棵草变成坑所需要的代价。

坑向T建边，容量为F，表示如果割掉坑和T的联系，将这个坑变成草所需要的代价。

然后所有相邻的两个点之间建无向边，容量为B，如果有流量从源点流向汇点，则必定是经过了（草->坑）边。

最后我们对最外围的草建边S-草，容量为无穷大，表示这个草一定不会变成坑（绝对不会割掉S-草边）

现在我们要做的就是将一些草变成坑（割掉S-草边），将一些坑变成草（割掉坑-T边）来使得最后从源点到汇点的流量最小。该最小流量的定义便是最小割。

其他小技巧

1、拆边（边权随流量的单调性）

【LA 5095】费用和流量的平方成正比的最小费用流最大流。容量c均为整数，每条弧有一个费用系数a，表示该弧流量为x时费用为ax^2。

建模：每条边按照容量大小x拆成x条，容量依次为a，3a，5a，7a......因为最小费用最大流每次一定是先走最小费用的边，所以走的一定是先选小的边，而前k小的边的权和正好是ak^2，和原题的要求等价。

【BZOJ 1449】给定

先差分，再拆边。

注意，输赢都有贡献，普通做法不行。直接当成那些比赛所有人都输，那只要计算赢的那个人的贡献。

然后差分：

赢k-1场：c[i]*(win[i]+(k-1))^2+d[i]*(sm[i]+lose[i]-(k-1))^2

赢k场：c[i]=(win[i]+k)^2+d[i]*(sm[i]+lose[i]-k)^2

相减得到赢第k场：c[i]*(2*win[i]-(2*k-1))-d[i]*(2*(lose[i]+sm[i])-(2*k-1))

这是单调的，所以把原本的贡献+最大费用流就好了。

2.网络中边权有正有负的最小费用流。

建模：如果没有负费用圈，则只需在增广到增广路费用为正时停止即可。如果存在负费用圈，则应该先用消圈法消去负圈。

3、二分+最大流

【HDU 3081】

n个女生与n个男生配对，每个女生只能配对某些男生，有些女生相互是朋友，每个女生也可以跟她朋友能配对的男生配对。

每次配对，每个女生都要跟不同的男生配对且每个女生都能配到对。问最多能配对几轮。(n<=100)

二分+最大流。二分答案，因为有单调性。然后直接最大流了。输入那里要用并查集。

4、增加中间点减少边数（边合并）

【BZOJ 4205】

现在有一种卡牌游戏，每张卡牌上有三个属性值：A,B,C。把卡牌分为X,Y两类，分别有n1,n2张。
两张卡牌能够配对，当且仅当，存在至多一项属性值使得两张卡牌该项属性值互质，且两张卡牌类别不同。
比如一张X类卡牌属性值分别是225,233,101，一张Y类卡牌属性值分别为115,466,99。那么这两张牌是可以配对的，因为只有101和99一组属性互质。
游戏的目的是最大化匹配上的卡牌组数，当然每张卡牌只能用一次。

解法：相当于至少两个属性不互质，但是直接建图然后匈牙利或者网络流都会超时。筛出200以内质数。新建点(2,2,x)等等表示前两个属性有2这个约数，连接起来，就好了。然后跑网络流。

一些经典题

【餐巾计划问题】bzoj1221