【Splay 总结】
很多年前学的splay已经忘了？
BZOJ 3729 要用Splay啊哭。。强制在线。。
二叉查找树
二叉排序树（Binary Sort Tree）又称二叉查找树（Binary Search Tree），亦称二叉搜索树。
伸展树是二叉查找树的一种改进，与二叉查找树一样，伸展树也具有有序性。
即伸展树中的每一个节点x都满足：该节点左子树中的每一个元素都小于x，而其右子树中的每一个元素都大于x。
与普通二叉查找树不同的是，伸展树可以自我调整，这就要依靠伸展操作Splay(x,S)。
旋转
1.zig ：
当目标节点为根节点的左/右节点时，进行单旋转。
2.zig-zag:
当目标节点与父节点和祖父节点构成zig-zag时，进行双旋转。
3.zig-zig:
当目标节点有父节点和祖父节点构成zig-zig时，进行一次zig-zig操作。
单旋转操作效果（以右单旋转为例）：
双旋转操作效果：
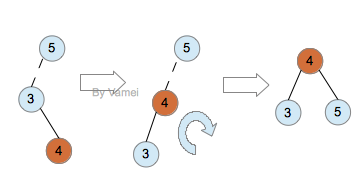
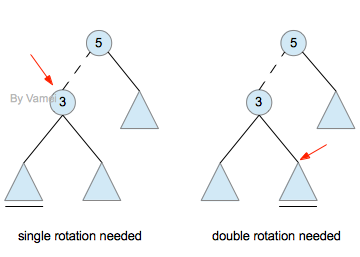
Zig-zig操作效果：
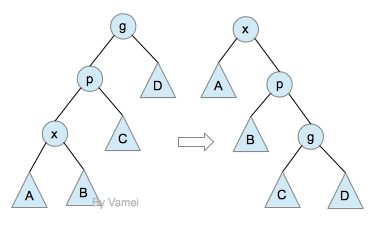
在Splay tree中，zig-zig操作基本上代替的AVL tree 中的单旋转。
伸展树的基本操作
利用Splay操作，我们可以在伸展树S上进行如下运算：
(1)Find(x,S)：判断元素x是否在伸展树S表示的有序集中。
首先，与在二叉查找树中的查找操作一样，在伸展树中查找元素x。如果x
在树中，则再执行Splay(x,S)调整伸展树。
(2)Insert(x,S)：将元素x插入伸展树S表示的有序集中。
首先，也与处理普通的二叉查找树一样，将x 插入到伸展树S中的相应位置
上，再执行Splay(x,S)。
(3)Delete(x,S)：将元素x从伸展树S所表示的有序集中删除。
首先，用在二叉查找树中查找元素的方法找到x的位置。如果x没有孩子或
只有一个孩子，那么直接将x删去，并通过Splay操作，将x节点的父节点调整
到伸展树的根节点处。否则，则向下查找x的后继y，用y替代x的位置，最后
执行Splay(y,S)，将y调整为伸展树的根。
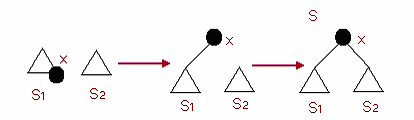
(4)Join(S1,S2)：将两个伸展树S1与S2合并成为一个伸展树。其中S1的所
有元素都小于S2的所有元素。
首先，我们找到伸展树S1 中最大的一个元素x，再通过Splay(x,S1)将x 调
整到伸展树S1 的根。然后再将S2 作为x 节点的右子树。这样，就得到了新的
伸展树S。如图所示
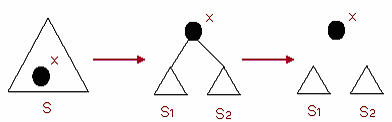
(5)Split(x,S)：以x 为界，将伸展树S 分离为两棵伸展树S1 和S2，其中S1
中所有元素都小于x，S2中的所有元素都大于x。
首先执行Find(x,S)，将元素x 调整为伸展树的根节点，则x 的左子树就是
S1，而右子树为S2。如图所示
除了上面介绍的五种基本操作，伸展树还支持求最大值、求最小值、求前趋、
求后继等多种操作，这些基本操作也都是建立在伸展操作的基础上的。
Splay模板题
[BZOJ3223] Tyvj 1729 文艺平衡树 关于翻转标记
[BZOJ3224] Tyvj 1728 普通平衡树平衡树基本操作
[BZOJ1503] [NOI2004]郁闷的出纳员带+-标记的平衡树
[BZOJ1208] [HNOI2004]宠物收养所
[BZOJ1251] 序列终结者注意标记下放的过程
