【BZOJ 3561】 3561: DZY Loves Math VI （莫比乌斯，均摊log）

 

3561: DZY Loves Math VI

Time Limit: 10 Sec  Memory Limit: 256 MB
Submit: 205  Solved: 141

Description

给定正整数n,m。求

Input

一行两个整数n,m。

Output

一个整数，为答案模1000000007后的值。

Sample Input

5 4

Sample Output

424

HINT

数据规模：

1<=n,m<=500000，共有3组数据。

Source

By Jcvb

 

 

【分析】

　　式子已经推出来了，然而后面。。。我觉得我学了假的数论。。。

　　好吧，推式子。。

　　下面省了一些

　　$$\sum_{i=1}^{n}\sum_{j=1}^{m} lcm(i,j)^{gcd(i,j)}$$

　　$$=\sum_{i=1}^{n}\sum_{j=1}^{m} {[\dfrac{i*j}{gcd(i,j)}]}^{gcd(i,j)}$$

　　$$=\sum_{d=1}^{min(n,m)}d^d \sum_{i'=1}^{n/d} \sum_{j'=1}^{m/d} (i'*j')^d [gcd(i',j')==1]$$

　　$$=\sum_{d=1}^{min(n,m)}d^d\sum_{d'=1}^{min(n,m)/d} \mu(d')\sum_{i'=1}^{\dfrac{n}{d*d'}}(i'*d')^d*\sum_{j'=1}^{\dfrac{n}{d*d'}}(j'*d')^d$$

 

$$如果你觉得上面难看就看下面吧$$

 

　　
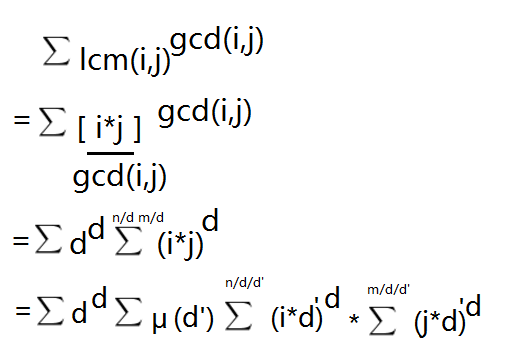
$$如果你觉得下面难看就看上面吧$$

 

 

 　

 1 #include<cstdio>
 2 #include<cstdlib>
 3 #include<cstring>
 4 #include<iostream>
 5 #include<algorithm>
 6 using namespace std;
 7 #define Mod 1000000007
 8 #define Maxn 500010
 9 #define LL long long
10 
11 int mymin(int x,int y) {return x<y?x:y;}
12 
13 int mu[Maxn],pri[Maxn],pl;
14 bool vis[Maxn];
15 
16 LL qpow(LL x,int b)
17 {
18     LL ans=1;
19     while(b)
20     {
21         if(b&1) ans=(ans*x)%Mod;
22         x=(x*x)%Mod;
23         b>>=1;
24     }
25     return ans;
26 }
27 
28 void init()
29 {
30     pl=0;
31     memset(vis,0,sizeof(vis));
32     mu[1]=1;
33     for(int i=2;i<=Maxn-10;i++)
34     {
35         if(!vis[i]) pri[++pl]=i,mu[i]=-1;
36         for(int j=1;j<=pl;j++)
37         {
38             if(i*pri[j]>Maxn-10) break;
39             vis[i*pri[j]]=1;
40             if(i%pri[j]==0) mu[i*pri[j]]=0;
41             else mu[i*pri[j]]=mu[i]*mu[pri[j]];
42             if(i%pri[j]==0) break;
43         }
44     }
45 }
46 
47 int a[Maxn],sum[Maxn];
48 void ffind(int n,int m)
49 {
50     int ans=0;
51     if(m>n) swap(m,n);
52     for(int i=1;i<=n;i++) a[i]=1;
53     for(int i=1;i<=m;i++)
54     {
55         int x=qpow(i,i),y=0;
56         for(int j=1;j*i<=n;j++)
57         {
58             a[j]=(LL)a[j]*j%Mod;
59             sum[j]=(sum[j-1]+a[j])%Mod;
60         }
61         for (int j=1;j*i<=m;j++)
62             y=((LL)a[j]*a[j]%Mod*sum[m/i/j]%Mod*sum[n/i/j]%Mod*mu[j]+y+Mod)%Mod;
63         ans=(ans+(LL)x*y%Mod)%Mod;
64     }
65     printf("%d\n",ans);
66 }
67 
68 int main()
69 {
70     int n,m;
71     init();
72     scanf("%d%d",&n,&m);
73     ffind(n,m);
74     return 0;
75 }
View Code

 

发现这个lych_cys大神的代码挺简短的，而且好像挺快的，LL都是算的时候才用。。

 

2017-03-23 21:56:35

posted @ 2017-03-23 21:41  konjak魔芋  阅读(237)  评论(0)  编辑  收藏  举报