【BZOJ 1095】 1095: [ZJOI2007]Hide 捉迷藏 （括号序列+线段树）
1095: [ZJOI2007]Hide 捉迷藏
Description
捉迷藏 Jiajia和Wind是一对恩爱的夫妻，并且他们有很多孩子。某天，Jiajia、Wind和孩子们决定在家里玩
捉迷藏游戏。他们的家很大且构造很奇特，由N个屋子和N-1条双向走廊组成，这N-1条走廊的分布使得任意两个屋
子都互相可达。游戏是这样进行的，孩子们负责躲藏，Jiajia负责找，而Wind负责操纵这N个屋子的灯。在起初的
时候，所有的灯都没有被打开。每一次，孩子们只会躲藏在没有开灯的房间中，但是为了增加刺激性，孩子们会要
求打开某个房间的电灯或者关闭某个房间的电灯。为了评估某一次游戏的复杂性，Jiajia希望知道可能的最远的两
个孩子的距离（即最远的两个关灯房间的距离）。 我们将以如下形式定义每一种操作： C(hange) i 改变第i个房
间的照明状态，若原来打开，则关闭；若原来关闭，则打开。 G(ame) 开始一次游戏，查询最远的两个关灯房间的
距离。Input
第一行包含一个整数N，表示房间的个数，房间将被编号为1,2,3…N的整数。接下来N-1行每行两个整数a, b，
表示房间a与房间b之间有一条走廊相连。接下来一行包含一个整数Q，表示操作次数。接着Q行，每行一个操作，如
上文所示。Output
对于每一个操作Game，输出一个非负整数到hide.out，表示最远的两个关灯房间的距离。若只有一个房间是关
着灯的，输出0；若所有房间的灯都开着，输出-1。Sample Input
8
1 2
2 3
3 4
3 5
3 6
6 7
6 8
7
G
C 1
G
C 2
G
C 1
GSample Output
4
3
3
4HINT
对于100%的数据， N ≤100000, M ≤500000。
Source
【分析】
此乃神题也。。今天的目标就是AC这题ORZ。。
跪%%%岛姐：
首先是括号表示法压压压：
比如这个图：
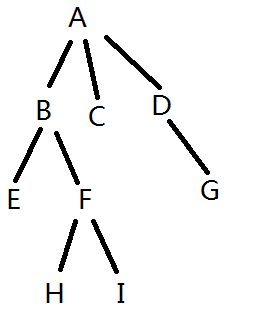是这样子的：[A[B[E][F[H][I]]][C][D[G]]]
去掉字母后的串：[[[][[][]]][][[]]]
对于两个点PQ,他们的距离是他们之间括号序列化简之后的括号数（画个图想想就能明白，‘[’表示下去，‘]’表示上去）
那么下面的操作就能用线段树维护了。
也就是说，题目只需要动态维护：max{a+b | S’(a, b) 是 S 的一个子串，且 S’ 介于两个黑点之间}，
这里 S 是整棵树的括号编码。我们把这个量记为 dis(s)。现在，如果可以通过左边一半的统计信息和右边一半的统计信息，得到整段编码的统计，这道题就可以用熟悉的线段树解决了。
这需要下面的分析。
考虑对于两段括号编码 S1(a1, b1) 和 S2(a2, b2)，如果它们连接起来形成 S(a, b)。
注意到 S1、S2 相连时又形成了 min{b, c} 对成对的括号，合并后它们会被抵消掉。（？..这里 b, c 应该分别是指 b1 和 a2。。。
所以：
当 a2 < b1 时第一段 [ 就被消完了，两段 ] 连在一起，例如： ] ] [ [ + ] ] ] [ [ = ] ] ] [ [ 当 a2 >= b1 时第二段 ] 就被消完了，两段 [ 连在一起，例如： ] ] [ [ [ + ] ] [ [ = ] ] [ [ [ （？..反了？。。。这样，就得到了一个十分有用的结论：
当 a2 < b1 时，(a,b) = (a1-b1+a2, b2)， 当 a2 >= b1 时，(a,b) = (a1, b1-a2+b2)。由此，又得到几个简单的推论：
(i) a+b = a1+b2+|a2-b1| = max{(a1-b1)+(a2+b2), (a1+b1)+(b2-a2)} (ii) a-b = a1-b1+a2-b2 (iii) b-a = b2-a2+b1-a1由 (i) 式，可以发现，要维护 dis(s)，就必须对子串维护以下四个量：
right_plus：max{a+b | S’(a,b) 是 S 的一个后缀，且 S’ 紧接在一个黑点之后} right_minus：max{a-b | S’(a,b) 是 S 的一个后缀，且 S’ 紧接在一个黑点之后} left_plus：max{a+b | S’(a,b) 是 S 的一个前缀，且有一个黑点紧接在 S 之后} left_minus：max{b-a | S’(a,b) 是 S 的一个前缀，且有一个黑点紧接在 S 之后}这样，对于 S = S1 + S2，其中 S1(a, b)、S2(c, d)、S(e, f)，就有
(e, f) = b < c ? (a-b+c, d) : (a, b-c+d) dis(S) = max{dis(S1), left_minus(S2)+right_plus(S1), left_plus(S2)+right_minus(S1), dis(S2)}那么，增加这四个参数是否就够了呢？
是的，因为：right_plus(S) = max{right_plus(S1)-c+d, right_minus(S1)+c+d, right_plus(S2)} right_minus(S) = max{right_minus(S1)+c-d, right_minus(S2)} left_plus(S) = max{left_plus(S2)-b+a, left_minus(S2)+b+a, left_plus(S1)} left_minus(S) = max{left_minus(S2)+b-a, left_minus(S1)}这样一来，就可以用线段树处理编码串了。实际实现的时候，在编码串中加进结点标号会更方便，对于底层结点，如果对应字符是一个括号或者一个白点，那 么right_plus、right_minus、left_plus、left_minus、dis 的值就都是 -maxlongint；如果对应字符是一个黑点，那么 right_plus、right_minus、left_plus、left_minus 都是 0，dis 是 -maxlongint。
现在这个题得到圆满解决，回顾这个过程，可以发现用一个串表达整棵树的信息是关键，这一“压”使得线段树这一强大工具得以利用.. .
转自：http://www.shuizilong.com/house/archives/bzoj-1095-zjoi2007hide-%E6%8D%89%E8%BF%B7%E8%97%8F/
猴赛雷啊！！！
表示即使如此，我还是纠结了好久ORZ。。
看代码吧、、
1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 #define Maxn 100010 8 #define INF 0xfffffff 9 10 int mymax(int x,int y) {return x>y?x:y;} 11 12 int a[Maxn]; 13 bool c[Maxn]; 14 int n; 15 16 struct node {int x,y,next;}t[2*Maxn];int len=0; 17 int first[Maxn]; 18 19 void ins(int x,int y) 20 { 21 t[++len].x=x;t[len].y=y; 22 t[len].next=first[x];first[x]=len; 23 } 24 25 struct nnode 26 { 27 int l,r,lc,rc; 28 int l1,r1,l2,r2,dis,c1,c2; 29 }tr[2*Maxn]; 30 31 int la[Maxn],lb[Maxn],dfn[Maxn]; 32 int na,nb,cnt,tot; 33 void dfs(int x,int f) 34 { 35 nb++;dfn[x]=++tot; 36 la[++cnt]=na;lb[cnt]=nb; 37 na=0;nb=0; 38 for(int i=first[x];i;i=t[i].next) if(t[i].y!=f) 39 { 40 int y=t[i].y; 41 dfs(y,x); 42 } 43 na++; 44 } 45 46 void upd(int x,int y) 47 { 48 tr[x].l1=tr[x].l2=tr[x].r1=tr[x].r2=-INF; 49 tr[x].dis=-INF; 50 tr[x].c1=la[y+1];tr[x].c2=lb[y+1]; 51 if(c[y+1]==1) tr[x].l1=la[y+1]+lb[y+1],tr[x].l2=lb[y+1]-la[y+1]; 52 if(c[y]==1) tr[x].r1=la[y+1]+lb[y+1],tr[x].r2=la[y+1]-lb[y+1]; 53 if(c[y]&&c[y+1]) tr[x].dis=tr[x].l1; 54 } 55 56 void merge(int x,int y,int z) 57 { 58 tr[z].dis=mymax(tr[x].dis,tr[y].dis); 59 tr[z].dis=mymax(tr[z].dis,mymax(tr[x].r1+tr[y].l2,tr[x].r2+tr[y].l1)); 60 61 int a=tr[x].c1,b=tr[x].c2,c=tr[y].c1,d=tr[y].c2; 62 63 if(b<c) tr[z].c1=a+c-b,tr[z].c2=d; 64 else tr[z].c1=a,tr[z].c2=b+d-c; 65 tr[z].l1=mymax(tr[x].l1,mymax(tr[y].l1-b+a,tr[y].l2+a+b)); 66 tr[z].l2=mymax(tr[x].l2,tr[y].l2+b-a); 67 tr[z].r1=mymax(tr[y].r1,mymax(tr[x].r1+d-c,tr[x].r2+c+d)); 68 tr[z].r2=mymax(tr[y].r2,tr[x].r2+c-d); 69 } 70 71 int build(int l,int r) 72 { 73 int x=++tot; 74 tr[x].l=l;tr[x].r=r; 75 if(l==r) 76 { 77 upd(x,l); 78 } 79 else 80 { 81 int mid=(l+r)>>1; 82 tr[x].lc=build(l,mid); 83 tr[x].rc=build(mid+1,r); 84 merge(tr[x].lc,tr[x].rc,x); 85 } 86 return x; 87 } 88 89 void change(int x,int y) 90 { 91 if(y<1||y>n) return; 92 if(tr[x].l==tr[x].r) 93 { 94 upd(x,tr[x].l); 95 return; 96 } 97 int mid=(tr[x].l+tr[x].r)>>1; 98 if(y<=mid) change(tr[x].lc,y); 99 else change(tr[x].rc,y); 100 merge(tr[x].lc,tr[x].rc,x); 101 } 102 103 char s[110]; 104 105 int main() 106 { 107 int bl; 108 scanf("%d",&n); 109 for(int i=1;i<=n;i++) c[i]=1; 110 bl=n; 111 memset(first,0,sizeof(first));len=0; 112 for(int i=1;i<n;i++) 113 { 114 int x,y; 115 scanf("%d%d",&x,&y); 116 ins(x,y);ins(y,x); 117 } 118 na=0,nb=0;cnt=0;tot=0;dfs(1,0); 119 n--; 120 tot=0;build(1,n); 121 int q; 122 scanf("%d",&q); 123 for(int i=1;i<=q;i++) 124 { 125 scanf("%s",s); 126 if(s[0]=='C') 127 { 128 int x; 129 scanf("%d",&x); 130 if(c[dfn[x]]) bl--; 131 else bl++; 132 c[dfn[x]]=c[dfn[x]]?0:1; 133 change(1,dfn[x]-1); 134 change(1,dfn[x]); 135 } 136 else 137 { 138 if(bl==0) printf("-1\n"); 139 else if(bl==1) printf("0\n"); 140 else printf("%d\n",tr[1].dis); 141 } 142 } 143 return 0; 144 }
2017-01-20 09:11:16
