【NOIP 2013 DAY2 T3】 华容道(spfa)
题目描述
【问题描述】
小 B 最近迷上了华容道,可是他总是要花很长的时间才能完成一次。于是,他想到用编程来完成华容道:给定一种局面, 华容道是否根本就无法完成,如果能完成, 最少需要多少时间。
小 B 玩的华容道与经典的华容道游戏略有不同,游戏规则是这样的:
在一个 n*m 棋盘上有 n*m 个格子,其中有且只有一个格子是空白的,其余 n*m-1个格子上每个格子上有一个棋子,每个棋子的大小都是 1*1 的;
有些棋子是固定的,有些棋子则是可以移动的;
- 任何与空白的格子相邻(有公共的边)的格子上的棋子都可以移动到空白格子上。
游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。
给定一个棋盘,游戏可以玩 q 次,当然,每次棋盘上固定的格子是不会变的, 但是棋盘上空白的格子的初始位置、 指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次
玩的时候, 空白的格子在第 EXi 行第 EYi 列,指定的可移动棋子的初始位置为第 SXi 行第 SYi列,目标位置为第 TXi 行第 TYi 列。
假设小 B 每秒钟能进行一次移动棋子的操作,而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间,或者告诉他不可能完成游戏。
输入输出格式
输入格式:
输入文件为 puzzle.in。
第一行有 3 个整数,每两个整数之间用一个空格隔开,依次表示 n、m 和 q;
接下来的 n 行描述一个 n*m 的棋盘,每行有 m 个整数,每两个整数之间用一个空格隔开,每个整数描述棋盘上一个格子的状态,0 表示该格子上的棋子是固定的,1 表示该格子上的棋子可以移动或者该格子是空白的。接下来的 q 行,每行包含 6 个整数依次是 EXi、EYi、SXi、SYi、TXi、TYi,每两个整数之间用一个空格隔开,表示每次游戏空白格子的位置,指定棋子的初始位置和目标位置。
输出格式:
输出文件名为 puzzle.out。
输出有 q 行,每行包含 1 个整数,表示每次游戏所需要的最少时间,如果某次游戏无法完成目标则输出−1。
输入输出样例
输入样例#1:
3 4 2 0 1 1 1 0 1 1 0 0 1 0 0 3 2 1 2 2 2 1 2 2 2 3 2输出样例#1:
2 -1说明
【输入输出样例说明】
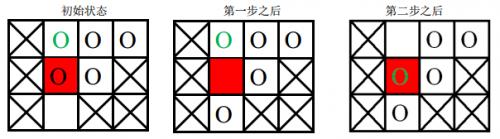
棋盘上划叉的格子是固定的,红色格子是目标位置,圆圈表示棋子,其中绿色圆圈表示目标棋子。
- 第一次游戏,空白格子的初始位置是 (3, 2)(图中空白所示),游戏的目标是将初始位置在(1, 2)上的棋子(图中绿色圆圈所代表的棋子)移动到目标位置(2, 2)(图中红色的格子)上。
移动过程如下:
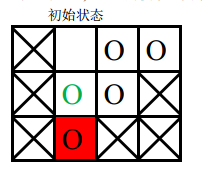
- 第二次游戏,空白格子的初始位置是(1, 2)(图中空白所示),游戏的目标是将初始位置在(2, 2)上的棋子(图中绿色圆圈所示)移动到目标位置 (3, 2)上。
要将指定块移入目标位置,必须先将空白块移入目标位置,空白块要移动到目标位置,必然是从位置(2, 2)上与当前图中目标位置上的棋子交换位置,之后能与空白块交换位置的只有当前图中目标位置上的那个棋子,因此目标棋子永远无法走到它的目标位置, 游戏无
法完成。
【数据范围】
对于 30%的数据,1 ≤ n, m ≤ 10,q = 1;
对于 60%的数据,1 ≤ n, m ≤ 30,q ≤ 10;
对于 100%的数据,1 ≤ n, m ≤ 30,q ≤ 500。
这题我只想到60分解法了。。
正解还是好机智,要注意500个q其实都是在同一个图上面的【想想这个有什么用就好了ORZ。。
copy题解:
编辑人:TsReaper 更新时间2015-08-18 14:48
考验状态记录技巧的一道好题!因为我们只要考虑指定块的位置,而指定块位置的移动和空白块有关,我们可以记录(x1,y1,x2,y2)表示指定块在(x1,y1),空白块在(x2,y2)的状态。由于空白块可以四方向移动,所以每个状态会向四个状态连边。这样共有(nm)^2个状态,总复杂度为O(q(nm)^2),只能通过60%的数据。
但是我们可以发现:只有空白块位于指定块的四方向上,指定块才可以移动。所以,我们可以记(x1,y1,dir)表示指定块在(x1,y1),空白块在指定块的dir方向(0表示上,1表示下什么的......)的状态。这样状态只有4nm个。
接下来我们考虑各个状态之间的连边。首先,空白块和指定块可以交换位置,这两个状态连边的边权为1;其次,假定空白块在指定块上方,空白块可以通过若干步移动来到空白块下/左/右方。这些状态连边的边权我们可以通过BFS计算出来。
这样就构造出了一张图,先把空白块移动到目标块旁边,之后向目标状态(空白块可以位于指定块的四个方向)做最短路即可。用spfa复杂度为O(qknm),可以通过100%的数据。
题解2:
这道题相当的坑,谁会想到NOIP最后一道题会考宽搜。(我一开始想成双连通分量了。。。)
宽搜。
可以发现,棋子要移动的前提是:它的四周有一个空格。因此状态总共只有2种决策:要么棋子与空格交换,要么空格在棋子周围的四个格子中自由移动。宽搜写起来也很方便。
那么现在问题来了,一组数据有多组询问,普通的宽搜是肯定要超时的,怎么办呢?
仔细一看就会发现这道题的特点:所有的询问都是在同一张图上进行的,而这张图又很小(30*30)。所以我们可以先预处理出所有点周围的空格在不经过它的情况下互相能够到达的最短路,这样每一次宽搜就相当于跑一次最短路了。(当然用SPFA最方便啊)
结合起来就完全明白了ORZ。。。

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 #include<queue> 7 #include<cmath> 8 using namespace std; 9 #define Maxn 35 10 #define INF 0xfffffff 11 12 int mymin(int x,int y) {return x<y?x:y;} 13 14 int a[Maxn][Maxn]; 15 int n,m,qs; 16 17 int bx[6]={0,1,-1,0}, 18 by[6]={-1,0,0,1}; 19 20 queue<int > q; 21 int d[Maxn*Maxn*4]; 22 int bfs(int x,int y,int xx,int yy) 23 { 24 while(!q.empty()) q.pop(); 25 memset(d,-1,sizeof(d)); 26 q.push((x-1)*m+y);d[(x-1)*m+y]=0; 27 while(!q.empty()) 28 { 29 int now=q.front(),nx,ny; 30 nx=now/m+1;ny=now%m;if(ny==0) ny=m,nx--; 31 if(nx==xx&&ny==yy) return d[now]; 32 for(int i=0;i<4;i++) if(a[nx+bx[i]][ny+by[i]]) 33 { 34 int nn=(nx+bx[i]-1)*m+ny+by[i]; 35 if(d[nn]==-1) 36 { 37 d[nn]=d[now]+1; 38 q.push(nn); 39 } 40 } 41 q.pop(); 42 } 43 return -1; 44 } 45 46 int num[Maxn][Maxn][5],cnt; 47 48 struct node 49 { 50 int x,y,c,next; 51 }t[Maxn*Maxn*40];int len; 52 int first[Maxn*Maxn*4]; 53 54 void ins(int x,int y,int c) 55 { 56 t[++len].x=x;t[len].y=y;t[len].c=c; 57 t[len].next=first[x];first[x]=len; 58 } 59 60 void init() 61 { 62 scanf("%d%d%d",&n,&m,&qs); 63 memset(a,0,sizeof(a)); 64 cnt=0; 65 for(int i=1;i<=n;i++) 66 for(int j=1;j<=m;j++) 67 { 68 scanf("%d",&a[i][j]); 69 } 70 for(int i=1;i<=n;i++) 71 for(int j=1;j<=m;j++) if(a[i][j]) 72 for(int k=0;k<4;k++) if(a[i+bx[k]][j+by[k]]) 73 { 74 num[i][j][k]=++cnt; 75 // printf("num_ %d %d %d = %d\n",i,j,k,num[i][j][k]); 76 } 77 len=0; 78 memset(first,0,sizeof(first)); 79 int i,j; 80 for(i=1;i<=n;i++) for(j=1;j<=m;j++) if(a[i][j]) 81 { 82 // printf("%d %d\n",i,j); 83 for(int k=0;k<4;k++) if(a[i+bx[k]][j+by[k]]) 84 { 85 a[i][j]=0; 86 for(int l=k+1;l<4;l++) if(a[i+bx[l]][j+by[l]]) 87 { 88 int x=bfs(i+bx[k],j+by[k],i+bx[l],j+by[l]); 89 if(x==-1) continue; 90 ins(num[i][j][k],num[i][j][l],x); 91 ins(num[i][j][l],num[i][j][k],x); 92 } 93 a[i][j]=1; 94 ins(num[i][j][k],num[i+bx[k]][j+by[k]][3-k],1); 95 ins(num[i+bx[k]][j+by[k]][3-k],num[i][j][k],1); 96 } 97 } 98 /*for(int i=1;i<=len;i+=2) 99 { 100 printf("%d -> %d = %d\n",t[i].x,t[i].y,t[i].c); 101 }*/ 102 } 103 104 int ex,ey,sx,sy,tx,ty; 105 bool pp[Maxn*Maxn*4],inq[Maxn*Maxn*4]; 106 int dis[Maxn*Maxn*4]; 107 108 int spfa(int st) 109 { 110 while(!q.empty()) q.pop(); 111 memset(dis,63,sizeof(dis)); 112 memset(inq,0,sizeof(inq)); 113 q.push(st);dis[st]=0;inq[st]=1; 114 int ans=INF; 115 while(!q.empty()) 116 { 117 int x=q.front(); 118 if(!pp[x]) 119 { 120 for(int i=first[x];i;i=t[i].next) 121 { 122 int y=t[i].y; 123 if(dis[y]>dis[x]+t[i].c) 124 { 125 dis[y]=dis[x]+t[i].c; 126 if(!inq[y]) 127 { 128 inq[y]=1; 129 q.push(y); 130 } 131 } 132 } 133 } 134 else ans=mymin(ans,dis[x]); 135 q.pop();inq[x]=0; 136 } 137 return ans; 138 } 139 140 void ffind() 141 { 142 memset(pp,0,sizeof(pp)); 143 for(int i=1;i<=qs;i++) 144 { 145 int ans=INF; 146 scanf("%d%d%d%d%d%d",&ex,&ey,&sx,&sy,&tx,&ty); 147 if(sx==tx&&sy==ty) printf("0\n"); 148 else 149 { 150 for(int j=0;j<4;j++) pp[num[tx][ty][j]]=1; 151 a[sx][sy]=0; 152 for(int j=0;j<4;j++) if(a[sx+bx[j]][sy+by[j]]) 153 { 154 int x=bfs(ex,ey,sx+bx[j],sy+by[j]); 155 // printf("%d %d %d = %d \n",sx,sy,j,x); 156 if(x==-1) continue; 157 x+=spfa(num[sx][sy][j]); 158 // printf("%d %d %d = %d \n",sx,sy,j,x); 159 ans=mymin(ans,x); 160 } 161 a[sx][sy]=1; 162 if(ans==INF) printf("-1\n"); 163 else printf("%d\n",ans); 164 for(int j=0;j<4;j++) pp[num[tx][ty][j]]=0; 165 } 166 167 } 168 } 169 170 int main() 171 { 172 init(); 173 ffind(); 174 return 0; 175 }
注意一开始就在终点的特判【我被坑了ORZ....
放个数据,答案是377

2016-11-16 09:38:27