【良心noip膜你赛】总结

一点都不良心！！！！

AK 快乐

爆零快乐！！！

1、

A、 value
512mb 1s
规定一个区间的价值为这个区间中所有数 and 起来的值与这个区间所有数 or 起
来的值的乘积。
例如 3 个数 2,3,6。它们 and 起来的值为 2， or 起来的值为 7，这个区间对答
案的贡献为 2*7=14。
现在有一个 n 个数的序列，想知道所有 n*(n+1)/2 个区间的贡献的和对
1000000007 取模后的结果是多少。
例如当这个序列为{3,4,5}时，那么区间[1,1],[1,2],[1,3],[2,2],[2,3],[3,3]的贡献
分别为 9,0,0,16,20,25。
Input
第一行一个数 n
接下来一行 n 个数 ai，表示这 n 个数(0<=ai<=10^9)。
Output
一行表示答案。
Input
3
4 5
Output
70
limit
%30 n<=1000
%100 n<=100000

我打的是nlog^2 拆位树状数组维护，f[i]表示区间i~现在循环到的点，的&值，g[i]表示|值。

然后记录最后连续有多少个1或者0，然后区间修改f和g。。

【慢且错不说话。。

正解是，不用拆位，也是维护f,g,然后当前f和g的不同的值只有logn个，并且是单调的，然后说可以用链表？[我觉得是单调队列啊ORZ。。

这样就nlogn了。。。

要不要放我的垃圾代码：

 1 #include<cstdio>
 2 #include<cstdlib>
 3 #include<cstring>
 4 #include<iostream>
 5 #include<algorithm>
 6 using namespace std;
 7 #define Maxn 100010
 8 #define Mod 1000000007
 9 #define LL long long
10 
11 LL a[Maxn];
12 LL f[3][Maxn],g[3][Maxn];
13 LL ct[40],lt[40];
14 LL n;
15 
16 void add(LL x,LL l,LL r,LL c)
17 {
18     if(l>r) return;
19     c%=Mod;
20     // printf("%lld %lld %lld %lld\n",x,l,r,c);
21     for(LL i=l;i<=n;i+=i&(-i))
22         f[x][i]=(f[x][i]+c)%Mod,g[x][i]=(g[x][i]+l*c)%Mod;
23     r++;
24     for(LL i=r;i<=n;i+=i&(-i))
25         f[x][i]=(f[x][i]+Mod-c)%Mod,g[x][i]=(g[x][i]+Mod-(r*c)%Mod)%Mod;
26 }
27 
28 LL gsum(LL x,LL l,LL r)
29 {
30     if(l>r) return 0;
31     // printf("ask:%lld %lld %lld ",x,l,r);
32     LL ans=0;
33     for(LL i=r;i>=1;i-=i&(-i))
34         ans=(ans+(r+1)*f[x][i]-g[x][i])%Mod;
35     l--;
36     for(LL i=l;i>=1;i-=i&(-i))
37         ans=(ans-(l+1)*f[x][i]+g[x][i])%Mod;
38     // printf("%lld\n",ans);
39     ans=(ans%Mod+Mod)%Mod;
40     return ans;
41 }
42 
43 int main()
44 {
45     LL ans=0;
46     scanf("%lld",&n);
47     for(LL i=1;i<=n;i++) scanf("%lld",&a[i]);
48     memset(f,0,sizeof(f));
49     memset(g,0,sizeof(g));
50     for(LL i=1;i<=30;i++) lt[i]=-1,ct[i]=n+1;
51     LL sum=0;
52     for(LL i=1;i<=n;i++)
53     {
54         for(LL j=1;j<=30;j++)
55         {
56             LL y=a[i]&(1LL<<j-1);
57             if(y==0)
58             {
59                 if(lt[j]!=0)
60                 {
61                     sum=sum-((1LL<<j-1)*gsum(1,ct[j],i-1))%Mod;
62                     sum=(sum%Mod+Mod)%Mod;
63         // printf("sum=%lld\n",sum);
64                     // add(2,ct[j],i-1,-(1LL<<j-1)*gsum(1,ct[j],i-1));
65                     add(0,ct[j],i-1,-(1LL<<j-1));
66                     lt[j]=0;ct[j]=i;
67                 }
68             }
69             else
70             {
71                 if(lt[j]!=1)
72                 {
73                     
74                     sum=sum+((1LL<<j-1)*gsum(0,ct[j],i-1))%Mod;
75                     sum=(sum%Mod+Mod)%Mod;
76         // printf("sum=%lld\n",sum);
77                     // add(2,ct[j],i-1,(1LL<<j-1)*gsum(0,ct[j],i-1));
78                     add(1,ct[j],i-1,(1LL<<j-1));
79                     lt[j]=1;ct[j]=i;
80                 }
81             }
82         }
83         add(0,i,i,a[i]);add(1,i,i,a[i]);
84         sum=(sum+a[i]*a[i])%Mod;
85         //add(2,i,i,(a[i]*a[i])%Mod);
86         ans=(ans+sum)%Mod;
87         // printf("sum=%lld\n",sum);
88         // ans=(ans+gsum(2,1,i))%Mod;
89         // printf("ans=%lld\n",ans);
90         ans=(ans%Mod+Mod)%Mod;
91     }
92     printf("%lld\n",ans);
93     return 0;
94 }

View Code

真的好丑的code的说。。

2、

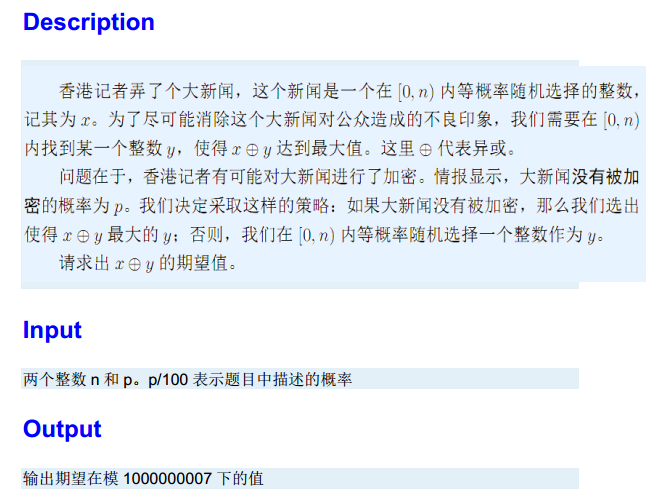
Sample Input
3 50
Sample Output
2

数位DP，数位DP，我打的数位DP太垃圾了，，又慢有错ORZ。。

不会告诉你我现在还没调出来，放弃治疗。。。

大数据还是错，应该是中间爆了吧ORZ。。。

233经过GDXB提点，终于AC了。。。。qpow爆了ORZ。。

  1 #include<cstdio>
  2 #include<cstdlib>
  3 #include<cstring>
  4 #include<iostream>
  5 #include<algorithm>
  6 using namespace std;
  7 // #define Mod 1000000007
  8 #define LL long long
  9 
 10 const LL Mod= 1000000007;
 11 
 12 LL n,p;
 13 LL f[70][2][2],g[70][2][2];
 14 LL get_ans1(int x,int fl1,int fl2)
 15 {
 16     if(x==0) return 0;
 17     LL ans=0;
 18     LL y=(n&(1LL<<x-1));
 19     if(y!=0) y=1;
 20     // if(!fl1&&!fl2&&f[x]!=-1) return f[x];
 21     if(f[x][fl1][fl2]!=-1) return f[x][fl1][fl2];
 22     LL add=(1LL<<x-1)%Mod,ad1=(n&((1LL<<x-1)-1))+1;
 23     if(y==1)
 24     {
 25         ans=(ans+get_ans1(x-1,0,fl2)+add*add)%Mod; //0 -> 1
 26         if(fl1) add=ad1;
 27         add%=Mod;
 28         ans=(ans+get_ans1(x-1,fl1,0)+((1LL<<x-1)%Mod)*add)%Mod;//1 -> 0
 29     }
 30     else //0
 31     {
 32         if(!fl1) ans=(ans+get_ans1(x-1,fl1,fl2)+add*add)%Mod; //1->0
 33         if(fl1) add=(n&((1LL<<x-1)-1))+1;
 34         add%=Mod;
 35         if(!fl2) ans=(ans+get_ans1(x-1,fl1,fl2)+add*((1LL<<x-1)%Mod))%Mod;//0->1
 36         else ans=(ans+get_ans1(x-1,fl1,fl2))%Mod;//0->0
 37     }
 38     f[x][fl1][fl2]=ans;
 39     // if(!fl1&&!fl2) f[x]=ans;
 40     return ans;
 41 }
 42 
 43 LL qpow(LL x,LL b)
 44 {
 45     x%=Mod;
 46     LL ans=1;
 47     while(b)
 48     {
 49         if(b&1) ans=(ans*x)%Mod;
 50         x=(x*x)%Mod;
 51         b>>=1;
 52     }
 53     return ans;
 54 }
 55 
 56 LL get_ans2(int x,int fl1,int fl2)
 57 {
 58     if(x==0) return 0;
 59     LL ans=0;
 60     LL y=(n&(1LL<<x-1));
 61     if(y!=0) y=1;
 62     // if(!fl1&&!fl2&&g[x]!=-1) return g[x];
 63     if(g[x][fl1][fl2]!=-1) return g[x][fl1][fl2];
 64     LL ad1=1LL<<x-1,ad2=(n&((1LL<<x-1)-1))+1,add=ad1;
 65     ad1%=Mod;ad2%=Mod;add%=Mod;
 66     if(y==1)
 67     {
 68         if(fl2) add=ad2;add%=Mod;
 69         ans=(ans+get_ans2(x-1,0,fl2)+((ad1*add)%Mod)*((1LL<<x-1)%Mod))%Mod; //0 -> 1
 70         ans=(ans+get_ans2(x-1,0,0))%Mod; //0 -> 0
 71         // if(fl1) add=(n&((1<<x-1)-1))+1;
 72         add=ad1;
 73         add%=Mod;
 74         if(fl1) add=ad2;
 75         add%=Mod;
 76         ans=(ans+get_ans2(x-1,fl1,0)+((add*ad1)%Mod)*((1LL<<x-1)%Mod))%Mod;//1 -> 0
 77         ans=(ans+get_ans2(x-1,fl1,fl2))%Mod;//1 -> 1
 78     }
 79     else //0
 80     {
 81         if(!fl1) 
 82         {
 83             if(!fl2) ans=(ans+get_ans2(x-1,fl1,fl2))%Mod; //1->1
 84             if(fl2) add=ad2;add%=Mod;
 85             ans=(ans+get_ans2(x-1,fl1,fl2)+((ad1*add)%Mod)*((1LL<<x-1)%Mod))%Mod; //1->0
 86         }
 87         // if(fl1) add=(n&((1<<x-1)-1))+1;
 88         add=ad1;
 89         if(fl1) add=ad2;
 90         add%=Mod;
 91         if(!fl2) ans=(ans+get_ans2(x-1,fl1,fl2)+((add*ad1)%Mod)*((1LL<<x-1)%Mod))%Mod;//0->1
 92         ans=(ans+get_ans2(x-1,fl1,fl2))%Mod;//0->0
 93     }
 94     // if(!fl1&&!fl2) g[x]=ans;
 95     ans%=Mod;
 96     g[x][fl1][fl2]=ans;
 97     return ans;
 98 }
 99 
100 int main()
101 {
102     int mx=0;
103     scanf("%lld%lld",&n,&p);
104     LL now=n,d,dd;
105     while(now) mx++,now/=2;
106     memset(f,-1,sizeof(f));
107     n--;
108     LL a1=get_ans1(mx,1,1),ans=0,a2;
109     // printf("---%lld\n",a1);
110     d=qpow(100,Mod-2);dd=qpow(n+1,Mod-2);
111     // ans=(ans+((a1*p)%Mod)*(qpow(100,Mod-2)*qpow(n,Mod-2))%Mod)%Mod;
112     a1=( ((d*p)%Mod)*((a1*dd)%Mod) )%Mod;
113     // printf("%lld\n",a1);
114     ans=(ans+a1)%Mod;
115     // printf("%lld\n",ans);
116     
117     
118     memset(g,-1,sizeof(g));
119     a2=get_ans2(mx,1,1);
120     // printf("---%lld\n",a2);
121     n++;
122     d=qpow(100,Mod-2);dd=qpow(((n%Mod)*(n%Mod))%Mod,Mod-2);
123     // ans=(ans+(a2*(100-p)%Mod)*(qpow(100,Mod-2))*qpow(n*n,Mod-2)%Mod)%Mod;
124     a2=( ((d*(100-p))%Mod)* ((a2*dd)%Mod) )%Mod;
125     ans=(ans+a2)%Mod;
126 
127     // ans=(ans%Mod+Mod)%Mod;
128     printf("%lld\n",ans);
129     return 0;
130 }

View Code

无视我的调试真的好丑。。

3、

Sample Input
5 3
1 2
1 3
2 4
4 5
2 2
4 1
2 3
Sample Output
313
HINT
1<=P<=N
1<=K<=N
%30
N<=2000
Q<=2000
%100
N<=100000
Q<=100000

啊，可持久化。。。

就是先算b在a上面，这个直接算

然后就是b在c下面，那么就是a->b->c这条链

然后对于dis[a,c]>=k 那么b有k个位置

对于dis[a,c]<k 有dis[a,c]个位置

算出dfs序，然后就是询问区间小于等于k的东西的值

我打的是字母树。。。

啊啊啊数据开小了就开心了！！真开心！！！

  1 #include<cstdio>
  2 #include<cstdlib>
  3 #include<cstring>
  4 #include<iostream>
  5 #include<algorithm>
  6 using namespace std;
  7 #define Maxn 200010
  8 #define Maxd 30
  9 
 10 struct node
 11 {
 12     int x,y,next;
 13 }t[Maxn*2];int len;
 14 int first[Maxn];
 15 
 16 void ins(int x,int y)
 17 {
 18     t[++len].x=x;t[len].y=y;
 19     t[len].next=first[x];first[x]=len;
 20 }
 21 
 22 int dep[Maxn],sm[Maxn],dfn[Maxn],rt[Maxn],cnt=0;
 23 void dfs(int x,int f)
 24 {
 25     dfn[x]=++cnt;dep[dfn[x]]=dep[dfn[f]]+1;
 26     rt[dfn[x]]=dfn[x];sm[dfn[x]]=1;
 27     for(int i=first[x];i;i=t[i].next) if(t[i].y!=f)
 28     {
 29         int y=t[i].y;
 30         dfs(y,x);
 31         sm[dfn[x]]+=sm[dfn[y]];
 32         rt[dfn[x]]=rt[dfn[y]];
 33     }
 34 }
 35 
 36 int rrt[Maxn];
 37 struct hp
 38 {
 39     int lc,rc,ct,f;
 40 }tr[Maxn*30];
 41 int tot=0;
 42 
 43 void upd(int x)
 44 {
 45     tr[x].lc=tr[x].rc=tr[x].ct=0;
 46 }
 47 
 48 void build()
 49 {
 50     int lt;
 51     tr[0].lc=tr[0].rc=tr[0].ct=0;
 52     rrt[0]=0;
 53     for(int i=1;i<=cnt;i++)
 54     {
 55         lt=rrt[i-1];
 56         rrt[i]=++tot;
 57         int now=rrt[i];
 58         int z=dep[i];
 59         for(int j=Maxd;j>=1;j--)
 60         {
 61             int x=(z&(1<<j-1));
 62             if(x!=0) x=1;
 63             if(x==0)
 64             {
 65                 tr[now].lc=++tot;upd(tot);
 66                 tr[now].rc=tr[lt].rc;
 67                 lt=tr[lt].lc;
 68                 tr[tot].ct=tr[lt].ct+1;
 69                 tr[tot].f=tr[lt].f+z;
 70                 now=tot;
 71             }
 72             else
 73             {
 74                 tr[now].rc=++tot;upd(tot);
 75                 tr[now].lc=tr[lt].lc;
 76                 lt=tr[lt].rc;
 77                 tr[tot].ct=tr[lt].ct+1;
 78                 tr[tot].f=tr[lt].f+z;
 79                 now=tot;
 80             }
 81         }
 82     }
 83 }
 84 
 85 int sum;
 86 int query(int l,int r,int x)
 87 {
 88     sum=0;int ans=0;
 89     l=rrt[l-1],r=rrt[r];
 90     for(int i=Maxd;i>=1;i--)
 91     {
 92         int y=x&(1<<i-1);
 93         if(y!=0) y=1;
 94         if(y==0)
 95         {
 96             r=tr[r].lc;
 97             l=tr[l].lc;
 98         }
 99         else
100         {
101             sum+=tr[tr[r].lc].ct-tr[tr[l].lc].ct;
102             ans+=(tr[tr[r].lc].f-tr[tr[l].lc].f);
103             r=tr[r].rc;
104             l=tr[l].rc;
105         }
106     }
107     return ans;
108 }
109 
110 int main()
111 {
112     int n,q;
113     scanf("%d%d",&n,&q);
114     len=0;
115     memset(first,0,sizeof(first));
116     for(int i=1;i<n;i++)
117     {
118         int x,y;
119         scanf("%d%d",&x,&y);
120         ins(x,y);ins(y,x);
121     }
122     dep[0]=0;
123     dfs(1,0);
124     build();
125     for(int i=1;i<=q;i++)
126     {
127         int p,k,ans=0;
128         scanf("%d%d",&p,&k);
129         if(dep[dfn[p]]-1>=k) ans+=k*(sm[dfn[p]]-1);
130         else ans+=(dep[dfn[p]]-1)*(sm[dfn[p]]-1);
131         
132         ans+=query(dfn[p]+1,rt[dfn[p]],k+1+dep[dfn[p]]);
133         ans+=k*(sm[dfn[p]]-1-sum)-dep[dfn[p]]*sum-sum;
134         
135         printf("%d\n",ans);
136     }
137     return 0;
138 }

View Code

改数据范围就A了smg！！！

垃圾的人生！！！坎坷！！！

2016-11-06 17:33:10

posted @ 2016-11-06 17:28 konjak魔芋阅读(342) 评论(0) 编辑收藏举报

刷新页面返回顶部

【良心noip膜你赛】总结

公告