【POJ 2152】 Fire (树形DP)
FireDescription
Country Z has N cities, which are numbered from 1 to N. Cities are connected by highways, and there is exact one path between two different cities. Recently country Z often caught fire, so the government decided to build some firehouses in some cities. Build a firehouse in city K cost W(K). W for different cities may be different. If there is not firehouse in city K, the distance between it and the nearest city which has a firehouse, can’t be more than D(K). D for different cities also may be different. To save money, the government wants you to calculate the minimum cost to build firehouses.Input
The first line of input contains a single integer T representing the number of test cases. The following T blocks each represents a test case.
The first line of each block contains an integer N (1 < N <= 1000). The second line contains N numbers separated by one or more blanks. The I-th number means W(I) (0 < W(I) <= 10000). The third line contains N numbers separated by one or more blanks. The I-th number means D(I) (0 <= D(I) <= 10000). The following N-1 lines each contains three integers u, v, L (1 <= u, v <= N,0 < L <= 1000), which means there is a highway between city u and v of length L.Output
For each test case output the minimum cost on a single line.Sample Input
5 5 1 1 1 1 1 1 1 1 1 1 1 2 1 2 3 1 3 4 1 4 5 1 5 1 1 1 1 1 2 1 1 1 2 1 2 1 2 3 1 3 4 1 4 5 1 5 1 1 3 1 1 2 1 1 1 2 1 2 1 2 3 1 3 4 1 4 5 1 4 2 1 1 1 3 4 3 2 1 2 3 1 3 3 1 4 2 4 4 1 1 1 3 4 3 2 1 2 3 1 3 3 1 4 2Sample Output
2 1 2 2 3Source
POJ Monthly,Lou Tiancheng
【题意】
在树上建消防站,要求每个节点离最近的消防站距离小于K,问最小花费。
【分析】
之前做过一道有点像的题。但那题是费用还跟最小距离有关的,并且树是特殊的logn层,每条边的边权都是1。当时的第二维是记录距离。
这题点数比较小,第二维是记录负责点。[其实我是看了陈启峰的论文的,但不是很懂,我说说自己的理解~
f[i][j]是i这棵子树,i的负责点是j的最小费用。g[i]表示i这棵子树,不知道谁是负责点的最小费用。(负责点可以是树上的任意位置)
转移方程:f[x][i]=min(f[y][i]-w[i],g[y])+w[i]。
看方程我们可以看出我们只把负责点是i的w[i]的重复计算去掉了,这好像会带来一个问题:
就是x有两个孩子y1,y2,可能y1和y2的负责点都不是x的负责点,但是y1,y2的负责点是同一个点,那么这个相同的负责点就会算了两次。
看图:
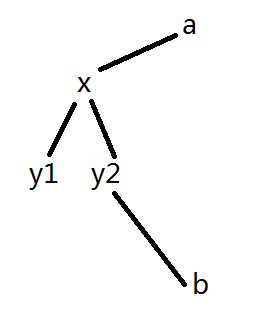
假设x的负责点是a,y1,y2的负责点是b。
情况1:b不在y1或y2的子树上,那么y1和y2走到b时必定经过x,那么x的负责点可以成为y1,y2的负责点,且费用更少了(这样子的负责点只计算一次)
情况2:b不在y1的子树上,在y2的子树上。那y1走到b也必定经过x。
若dis[x][a]>dis[x][b],那么x的负责点可以变成b,且费用更少。这个方案在f[x][b]中会算到。
若diis[x][a]<dis[x][b],那么y1的负责点可以变成a,且这样子a的负责费用只会计算一次。(反过来也一样就不说了)
好像就是这样。。吧。。
感觉这种跟树上的路径长度啊有关的东西,都有一些特殊的东西,就是你经过父亲走的时候,有些情况是可以不予考虑的,减掉这些情况,dp打起来就会简单得多了。
代码如下:

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 #define Maxn 1010 8 9 struct node 10 { 11 int x,y,c,next; 12 }t[2*Maxn];int len; 13 int first[Maxn]; 14 int n,w[Maxn],d[Maxn]; 15 16 void ins(int x,int y,int c) 17 { 18 t[++len].x=x;t[len].y=y;t[len].c=c; 19 t[len].next=first[x];first[x]=len; 20 } 21 22 int mymin(int x,int y) {return x<y?x:y;} 23 int mymax(int x,int y) {return x>y?x:y;} 24 25 int dis[Maxn][Maxn]; 26 27 void get_dis(int st,int x,int f) 28 { 29 for(int i=first[x];i;i=t[i].next) if(t[i].y!=f) 30 { 31 int y=t[i].y; 32 dis[st][y]=dis[st][x]+t[i].c; 33 get_dis(st,y,x); 34 } 35 } 36 37 int f[Maxn][Maxn],g[Maxn]; 38 void ffind(int x,int fa) 39 { 40 for(int i=first[x];i;i=t[i].next) if(t[i].y!=fa) 41 { 42 int y=t[i].y; 43 ffind(y,x); 44 } 45 for(int i=1;i<=n;i++) if(dis[x][i]<=d[x]) 46 { 47 f[x][i]=w[i]; 48 for(int j=first[x];j;j=t[j].next) if(t[j].y!=fa) 49 { 50 int y=t[j].y; 51 f[x][i]+=mymin(f[y][i]-w[i],g[y]); 52 } 53 g[x]=mymin(g[x],f[x][i]); 54 } 55 } 56 57 int main() 58 { 59 int T; 60 scanf("%d",&T); 61 while(T--) 62 { 63 scanf("%d",&n); 64 len=0; 65 memset(first,0,sizeof(first)); 66 for(int i=1;i<=n;i++) scanf("%d",&w[i]); 67 for(int i=1;i<=n;i++) scanf("%d",&d[i]); 68 for(int i=1;i<n;i++) 69 { 70 int x,y,c; 71 scanf("%d%d%d",&x,&y,&c); 72 ins(x,y,c);ins(y,x,c); 73 } 74 for(int i=1;i<=n;i++) 75 { 76 dis[i][i]=0; 77 get_dis(i,i,0); 78 } 79 memset(f,63,sizeof(f)); 80 memset(g,63,sizeof(g)); 81 ffind(1,0); 82 printf("%d\n",g[1]); 83 } 84 return 0; 85 }
2016-10-17 09:06:04


 浙公网安备 33010602011771号
浙公网安备 33010602011771号